
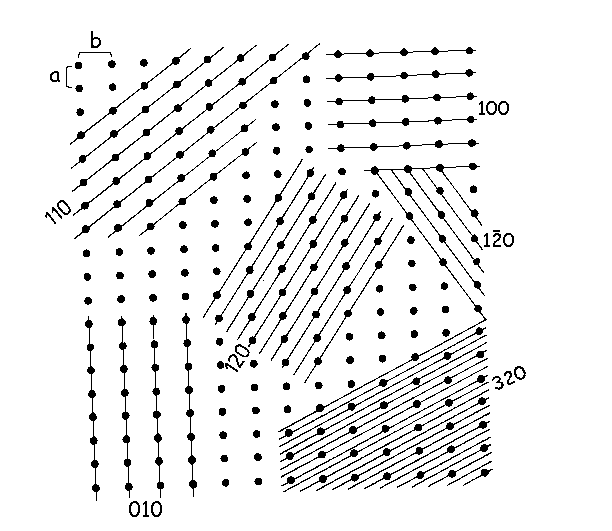
(1 1 1)
(1 1 2)
(-1 1 1)
Lekce I
| Úvod | ||
| Obsah lekce | ||
|
|
||
|
|
||
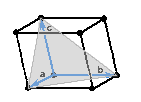
| Test | Rovina na obrázku má Millerovy indexy
(1 1 1) |
 |
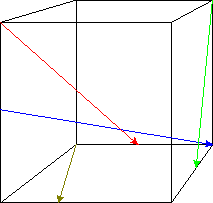
| Úloha | Zadejte indexy vyznačených směrů (červený, modrý, zelený, hnědý) |  |
Lekce II
| Obsah lekce | ||
|
|
|
|
| Test | 4-četné rotační ose vyhovuje mříž
čtvercová |
|
| Úloha |
|
V přiložených vzorech zvolte vhodně základní buňku a určete rovinnou mříž. Obrázek zadání si uložte, dokreslete vhodnou buňku a odešlete takto upravený obrázek. Odpovězte zároveň o jakou se jedná mříž.
|
Lekce III
| Obsah lekce | |||||||
|
(grupa pg)
|
 |
||||||
| Test 1 | Inverzní osa je složený prvek symetrie, jejíž
operace symetrie sestává
z několika otáčení a několika inverzí, na pořadí nezáleží
|
||||||
| Test 2 |
Na zadaných vzorech zvolte základní buňky a vyznačte prvky symetrie. Dále přiřaďte podle obsažených prvků symetrie příslušnou rovinnou grupu ze seznamu 17 možných grup. Do zadaných obrázků zakreslete v nějakém kreslícím programu polohu os symetrie (s využitím symbolů níže), rovin zrcadlení (zeleně resp. plnou čarou), případně skluzových rovin zrcadlení (modře resp. čárkovaně) Symboly pro osy symetrie:
|
Řešení: lze nalézt 2 systémy skluzových rovin a dvojčetné osy symetrie. Buňka je primitivní. Porovnáním se seznamem rovinných grup je zřejmé, že se jedná o grupu p2gg. |
|||||
| Úloha |
Lekce IV
| Obsah lekce | ||
| Základní typy krystalových struktur - prvky | 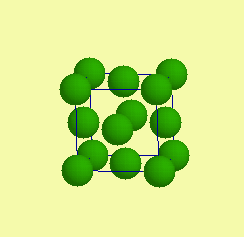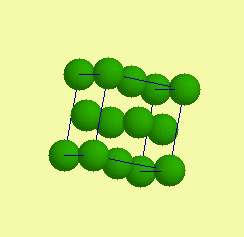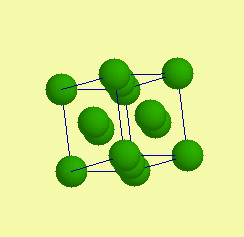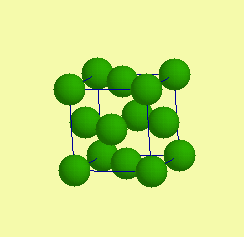 |
|
| Základní typy krystalových struktur - polární struktury | 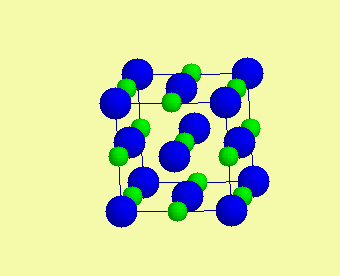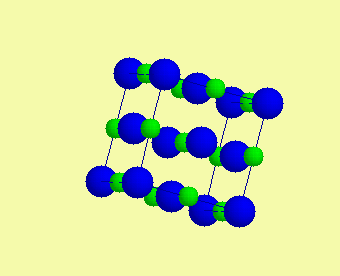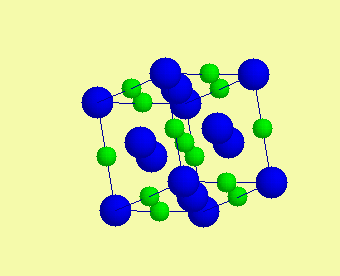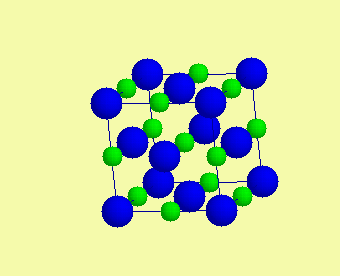 |
|
| Základní typy krystalových struktur - binární slitiny | 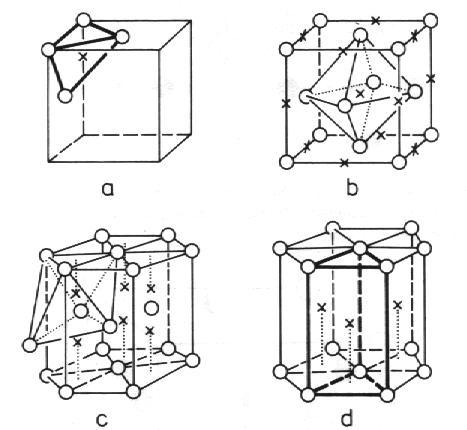 |
|
| Test | Předpokládejme, že máme rovinu zcela vyplněnou
stejnými kroužky. Které uspořádání má větší koeficient zaplnění,
šestičetné či čtyřčetné?
obě uspořádání jsou stejně zaplněna |
|
| Úloha | Nalezněte na Internetu strukturní údaje systému Fe - Pt a zobrazte strukturu. |
Lekce V
| Geometrické principy difrakce | ||
| Difrakce na monokrystalech |
|
|
| Difrakce na polykrystalech |  |
|
| Test |
|
|
Lekce VI
| Příprava na exkurzi - pěstování krystalů | ||
|
|
||
|
|
||
Java applety jsou převzaty z CD učebnice C. Giacovazzo:
Fundamentals of Crystallography a od
Steffena Webera.
Pro jejich spuštění musí být povoleny v prohlížeči a nainstalován příslušná Java
podpora..