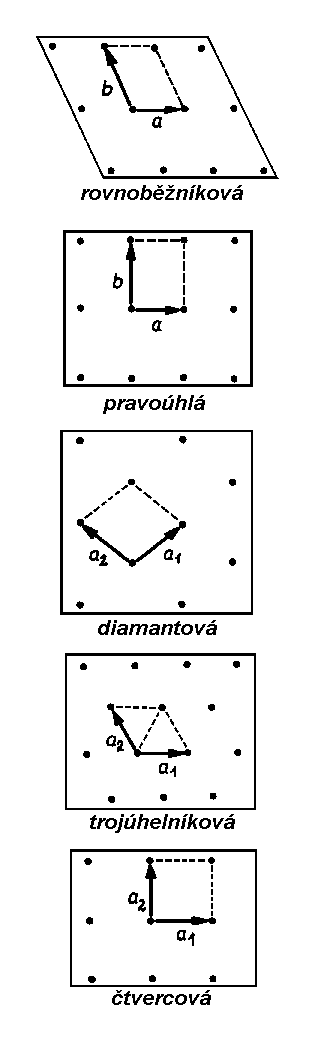
Existuje pouze pět různých typů rovinných mříží, tyto mříže vyhovují operacím symetrie prvků 1, 2, 3, 4, 6 a m. Nejobecnější rovinná mříž - rovnoběžníková - je v souladu s 1 a 2. Rovina zrcadlení m vyžaduje kolmost řad mřížových bodů k m a této podmínce vyhovuje mříž pravoúhlá a diamantová. Trojúhelníková mříž s úhlem mezi osami 120° vyhovuje 3 a 6 a čtvercová mříž je konzistentní se 4. Osy otáčení a roviny zrcadlení jsou kolmé k rovině mříže. Mříže s vyšší symetrií obsahují též prvky symetrie mříží o nižší symetrii.
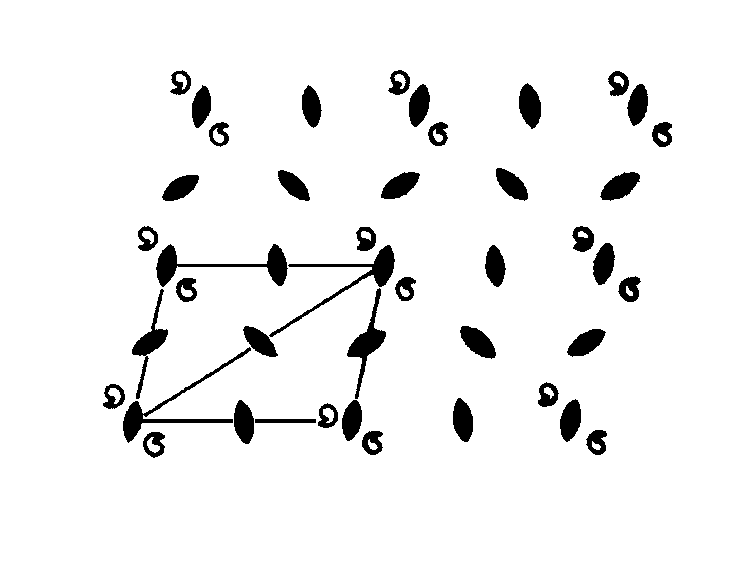 Trojrozměrné mříže bychom nyní mohli vytvářet
vrstvením rovinných mříží nad sebou. To je možné provést více způsoby.
Přítomnost některých rpvků symetrie si vynucuje existenci dalších.
Trojrozměrné mříže bychom nyní mohli vytvářet
vrstvením rovinných mříží nad sebou. To je možné provést více způsoby.
Přítomnost některých rpvků symetrie si vynucuje existenci dalších.
Povšimněme si nejprve rozložení os otáčení v rovinných mřížích. Je-li kombinována rotační osa s kolmým posunem, musí existovat i rotační osa rovnoběžná s výchozí. To znamená, že např. rovnoběžníková rovinná mříž, konzistentní s 2četnými osami umístěnými v mřížových bodech, je konzistentní ještě s dalšími 2četnými osami umístěnými mimo mřížové body v důsledku kombinace původních os s translacemi mříže. Rozmístění těchto os pochopíme snadno, obklopíme-li translačně ekvivalentní 2četné osy, tj. osy umístěné v mřížových bodech, asymetrickým motivem. Je patrné, že musí existovat i 2četné osy umístěné uprostřed mezi translačně ekvivalentními osami. Často tak přítomnost určitých prvků symetrie vyvolá automatickou přítomnost dalších.
Podobně bychom mohli
postupovat i u ostatních rovinných mříží. Kombinace prvků symetrie s
translacemi rovinných mříží se nazývají rovinné grupy a
existuje 17 typů rozdílných rovinných grup. Tři z nich jsou znázorněny na
obrázku níže. Je z něj patrno, že nově vzniklé rotační osy mohou mít i jinou
četnost než původní (o tom se lze opět přesvědčit pomocí opakovaných
motivů). Symboly naznačují polohu prvků symetrie v mříži. U obrázku jsou
tedy čtyřčetné osy ve středu a rozích čtverce. Pootočením čtverce
kolem nich o 90 stupňů dostaneme stejný vzor.
Kromě toho existují ještě dvojčetné osy na stranách čtverce.
Trojrozměrné mříže si můžeme představit jako sled rovinných mříží vzniklý periodickým opakováním těchto rovinných mříží translací ve třetím rozměru. V případě rovnoběžníkové mříže, konzistentní s 1, můžeme další rovinnou mříž umístit nad výchozí do libovolné polohy a získáme tak nejobecnější prostorovou mříž. Její primitivní buňka je rovnoběžnostěn s nestejnými délkami hran a s nestejnými úhly mezi nimi. Tímto postupem získáme všechny možné trojrozměrné mříže.
Soubor prvků symetrie krystalu se nazývá bodová grupa a prostorová mříž krystalu musí být v souladu s jeho bodovou grupou. Dá se ukázat, že existují určité prvky symetrie společné vždy pro určitou skupinu bodových grup, což vede k přirozenému rozdělení krystalů do krystalových soustav podle těchto společných prvků symetrie. Krystalové soustavy byly vzhledem ke své užitečnosti pojmenovány. Jsou uvedeny v tabulce (názvosloví není zcela jednotné, v závorce jsou uvedeny ekvivalenty) spolu se společnými minimálními prvky symetrie, což jsou minimální symetrie postačující k zařazení krystalu do dané krystalové soustavy - jsou diagnostickými prvky každé soustavy. Zjistíme-li tedy například přítomnost čtyřčetných a trojčetných os, je zřejmé, že krystal patří do kubické soustavy. Šestičetná osa zařazuje jednoznačně krystal do hexagonální soustavy.
| krystalová soustava | minimální symetrie |
|---|---|
| triklinická (trojklonná) | žádná |
| monoklinická (jednoklonná) | jedna 2četná osa podél c |
| ortorombická (rombická, kosočtverečná) |
tři 2četné osy podél a, b , c |
| tetragonální (čtverečná) | jedna 4četná osa podél c |
| kubická (izometrická) | čtyři 3četné osy podél tělesových úhlopříček krychle |
| hexagonální (šesterečná) | jedna 6četná osa podél c |
| trigonální (romboedrická, klencová) |
jedna 3četná osa podél hexagon. buňky |
Dá se dokázat (např. systematickým vyšetřováním možných způsobů
vrstvení rovinných mříží), že existuje pouze 14 různých
prostorových mříží. Nazývají se také Bravaisovy
mříže podle autora prvního úplného odvození (r. 1850). Každý
krystal lze tak musí mít být charakterizován jednou z těchto mříží
(jejím opakováním ve všech třech směrech vznikne krystal).
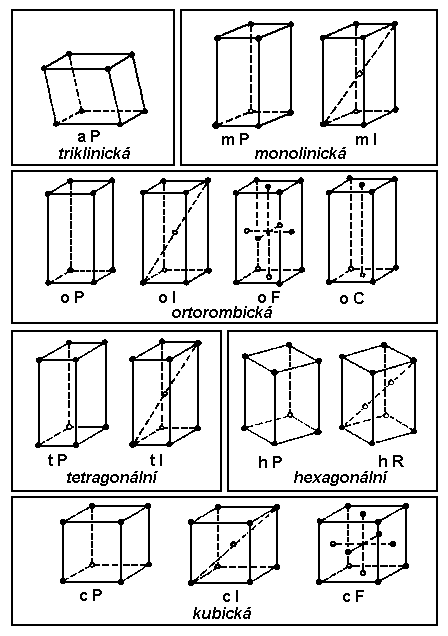 Na
obrázku jsou znázorněny konvenční buňky 14 prostorových mříží.
Na
obrázku jsou znázorněny konvenční buňky 14 prostorových mříží.
V tabulce jsou prostorové mříže rozděleny do šesti krystalových rodin v důsledku přiřazení mříží konzistentních s 3 k hexagonální soustavě, i když by podle symetrie příslušely k soustavě trigonální. Důvod tohoto přiřazení spočívá v tom, že při klasifikaci mříží je rozhodující typ mříže spíše než minimální symetrie. Daným přiřazením se dosáhne jednotnosti popisu mříží konzistentních s 3 pomocí jediného systému os.
Symboly P, A, B, C, I, F a R značí tzv. centrování buňky. Příslušné souřadnice jsou v následující tabulce. Smysl je patrný z obrázku.
| Symbol | Typ centrování | Souřadnice mřížových bodů v buňce |
|---|---|---|
| P | primitivní | 0, 0, 0 |
| C | bazálně centrovaná | 0, 0, 0; 1/2, 1/2, 0 |
| A | bazálně centrovaná | 0, 0, 0; 0, 1/2, 1/2 |
| B | bazálně centrovaná | 0, 0, 0; 1/2, 0, 1/2 |
| I | prostorově centrovaná | 0, 0, 0; 1/2, 1/2, 1/2 |
| F | plošně centrovaná | 0, 0, 0; 1/2, 1/2, 0; 0, 1/2, 1/2; 1/2, 0, 1/2 |
| R | romboedricky centrovaná vzhledem k hexagonálním osám |
0, 0, 0; 2/3, 1/3, 1/3; 1/3, 2/3, 2/3 |
primitivní vzhledem k romboedrickým osám |
0, 0, 0 |
Charakteristiky jednotlivých soustav jsou v následující tabulce.
| Krystalová rodina |
Symbol | Krystalová soustava | Konvenční soustava souřadnic | Bravaisovy mříže | |
| omezení parametrů mříže | určované parametry | ||||
| triklinická (trojklonná) |
a | triklinická | žádné | a, b, c a, b, g |
aP |
| monoklinická (jednoklonná) |
m | monoklinická | význačná osa b a = g = 90° |
a, b, c b |
mP mC (mA, mI) |
| význačná osa c a = b = 90° |
a, b, c g |
mP mA (mB, mI) |
|||
| ortorombická |
o | ortorombická | a = b = g = 90° | a, b, c | oP oC (oA, oB) oI oF |
| tetragonální | t | tetragonální | a = b a = b = g = 90° |
a, c | tP tI |
| hexagonální (šesterečná) |
h | trigonální | a = b a = b = 90° g = 120° (hexagonální osy) |
a, c | hP |
| a = b = c a = b = g (romboedrické osy) |
a, a | hR | |||
| hexagonální | a = b a = b = 90° g = 120° |
a, c | hP | ||
| kubická | c | kubická | a = b = c a = b = g = 90° |
a | cP cI cF |
Odkazy v pravém sloupci jsou klikací. Objeví se příslušná základní buňka, se kterou je možné otáčet.