STRUKTURY

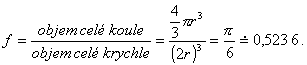
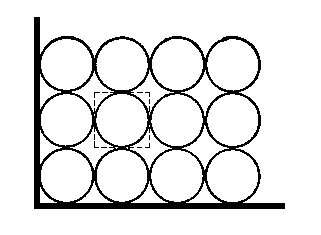
Zkoumejme otázku: Jak lze v prostoru nejtěsněji uspořádat stejně velké tvrdé koule? Bez ladu a skladu vzniknou zřejmě zbytečné mezery. Zkusme tedy koule naskládat pravidelně. Potom koule vyplňují celý prostor v poměru

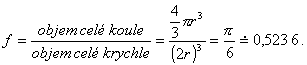Jelikož r³ se ve zlomku zkrátí, nezáleží vůbec na velikosti koulí. Vypočítali jsme tzv. koeficient zaplnění f.

Zatím umíme prostor vyplnit jen z 52,36%. Zkusme tedy vystavit čtvercovou pyramidu. Koule v rovinné vrstvě vytvářejí v mezerách mezi sebou hluboké čtyřcípé dolíky. Do každého z nich lze uložit kouli další vrstvy, která pak bude zase těsně čtvercově uspořádaná. Třetí vrstva bude opět nad vrstvou první atd., tj. vrstvy se budou střídat podle schématu 1-2-1-2.

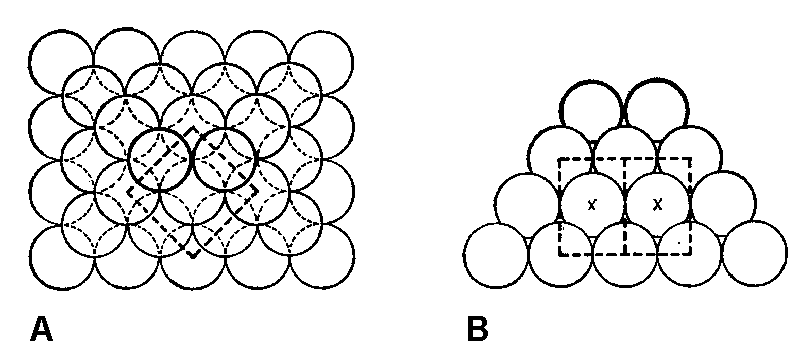
Čtvercová pyramida ze stejných koulí (A) v půdorysu, (B) z boku. Vyznačena též základní buňka.

Z obrázku je vidět, že středy kuliček tvoří plošně centrovanou mřížku. Dále si spočítáme koeficient zaplnění. Je-li objem základní buňky V₀ = a³, pak objem koulí, jež do ní patří, bude

(na buňku připadají 4 koule). Jelikož

dostáváme

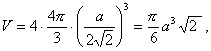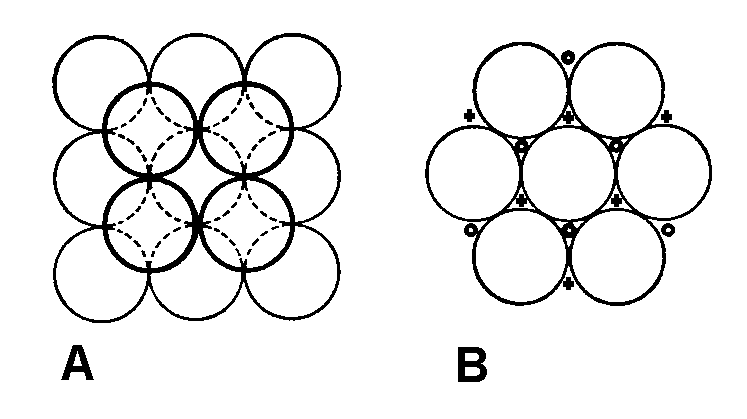
Všimněme si ještě, že stěny čtvercové pyramidy jsou rovinné, kuličky jsou v těchto rovinách těsně uspořádány a každá kulička má 6 přímých sousedů

Uspořádání koulí v rovinné vrstvě: (A)čtvercové, (B) šestiúhelníkové ("plástvovité").

Čtvercovou pyramidu jsme stavěli ze čtvercových vrstev (A), ale mnohem menší mezery mají rovinné šestičetné vrstvy (B) (je to dokonce nejtěsnější uspořádání v rovině). Takovéto vrstvy můžeme také klást na sebe; u třetí vrstvy však máme dvě možnosti - viz obr. 6.4. Buď bude třetí vrstva přesně nad první (tj. v poloze "1") nebo bude vůči ní pootočena (poloha "3").


Ukládání dalších plástvovitých vrstev: u druhé vrstvy je jediná možnost (A), u třetí dvojí, která odpovídá uspořádání hexagonálnímu (B) nebo kubickému (C).	Kubické plošně centrované uspořádání.	Hexagonální nejtěsnější uspořádání.

To, že jsme na stěně čtvercové pyramidy (B) "nalezli" šestičetnou vrstvu, není náhoda. Platí totiž, že čtvercová pyramida přesně odpovídá ukládání šestičetných vrstev v pořadí 1-2-3-1-2-3-1... ; je tedy jedno, který z těchto dvou způsobů použijeme, výsledek bude týž.

Uspořádání se sledem vrstev 1-2-1-2-1... se nazývá hexagonální nejtěsnější uspořádání (obr. 6.5) a se sledem 1-2-3-1-2-3... kubické plošně centrované uspořádání (obr. 6.6). Protože kubické plošně centrované uspořádání odpovídá čtvercové pyramidě, mají také stejný koeficient zaplnění. A protože hexagonální nejtěsnější uspořádání je ze zjevných příčin stejně zaplněné jako kubické plošně centrované uspořádání, bude mít také stejný koeficient zaplnění. Všechna tři uspořádání (z toho dvě identická) mají tedy koeficient zaplnění f = 0,7405 a dá se ukázat, že většího čísla se docílit nedá.

Zmiňme se ještě o jedné veličině, jež stejně jako koeficient zaplnění popisuje "těsnost" uspořádání. Jmenuje se koordinační číslo a je to počet nejbližších sousedů dané koule (atomu). Koordinační číslo primitivního kubického uspořádání je 6, hexagonálního nejtěsnějšího uspořádání a kubického plošně centrovaného uspořádání je 12.

Hledanou odpovědí na otázku v úvodu kapitoly je uspořádání pomocí plástvovitých rovinných vrstev kladených na sebe. V přírodě tomuto nejúspornějšímu uspořádání odpovídá asi 60% všech prvků a přibližně dvě třetiny krystalických prvků při pokojové teplotě. Většina prvků tedy respektuje požadavek minimální (potenciální) energie (my jsme vlastně zkoumali požadavek minimálního objemu), ale zbylých 40% prvků (+ ostatní látky, o nichž jsme nemluvili) ukazuje, že tento požadavek není jediným kritériem ( musíme počítat se směrovými vazbami apod.).