GEOMETRICKÉ PRINCIPY DIFRAKCE

Základní metodou pro určování krystalových struktur je rentgenová případně neutronová difrakce. Jedná se o analogii difrakce (ohybu) viditelného světla na optické mřížce. Ohybem a interferencí (skládáním) světelných vln dostáváme tzv. difrakční obraz vykazující maxima intenzity. Tento obraz je vlastně matematickou transformací objektu, na kterém dochází k difrakci. Z rozmístění maxim a jejich intenzit pak lze získat informaci o struktuře tohoto objektu (např. vzdálenosti vrypů mřížky apod.). Základní podmínkou pro to, aby byl efekt pozorovatelný je srovnatelná velikost vlnové délky světla s rozměry objektu. Snížíme-li vlnovou délku do oblasti meziatomových vzdáleností, tedy do oblasti rentgenového záření (10^-10 m), je možné metodu použít ke zjištení poloh atomů v základním stavebním kamenu krystalických látek - základní buňce.

1. Reciproká mříž

Pro interpretaci difrakčních experimentů je užitečné zavést pojem reciproké ("obrácené") mříže.
Při konstrukci reciproké mříže postupujeme následujícím způsobem:
1. Ze společného počátku vedeme kolmice ke každé osnově rovin (hkl)
2. Osnově rovin (hkl) odpovídá v reciproké mříži mřížový bod umístěný na normále ve vzdálenosti 1/d_hkl , kde d_hkl je mezirovinná vzdálenost v přímé mříži.

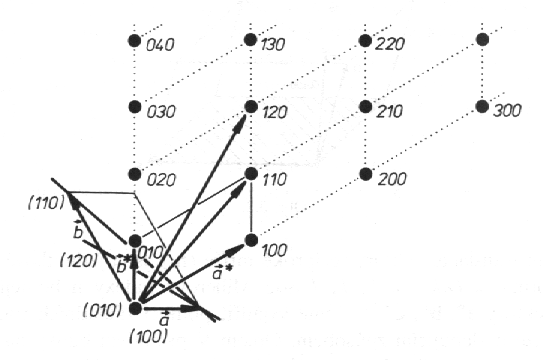
Každý mřížový bod reciproké mříže tak reprezentuje základní vlastnosti osnov rovin, tj. jejich orientaci a mezirovinné vzdálenosti. Je zřejmé, že body 100, 200, 300, ... budou ležet na jedné přímce, neboť roviny (100), (200), (300), ... jsou rovnoběžné. Tyto body leží v ekvidistantních vzdálenostech 1 / d₁₀₀ , neboť d₂₀₀ = d₁₀₀ / 2 , d₃₀₀ = d₁₀₀ / 3 atd.

Grafická konstrukce reciproké mříže k primitivní přímé mříži (osa c kolmá k nákresně).

Libovolný mřížový bod reciproké mříže můžeme popsat vektorem

G_hkl = ha^* + kb^* + lc^* ,

kde

a^* = n₁₀₀ / d₁₀₀ ,
b^* = n₀₁₀ / d₀₁₀ ,
c^* = n₀₀₁ / d₀₀₁

jsou základní translační vektory reciproké mříže (n_hkl jsou jednotkové vektory ve směrech normál k (hkl) a h, k, l jsou tzv. Millerovy indexy nebo jejich celistvé násobky.

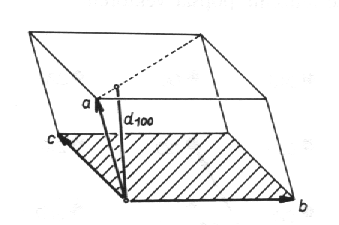Pro konstrukci reciproké mříže je užitečné si uvědomit, že vektor a^* je vždy kolmý k vektorům b a c a totéž platí cyklicky i o dalších vektorech. Odtud také plyne, že vektor a^* může být rovnoběžný s vektorem a pouze tehdy, když a je kolmý k b a c .

Reciprokou mříž k centrované přímé mříži můžeme zkonstruovat pomocí primitivní buňky.

Konstrukce reciproké mříže k centrované mříži definované základními translacemi a, b, c (osa c kolmá k nákresně). Čárkovaně je vyznačena primitivní buňka v přímé mříži. Prázdné kroužky znázorňují mřížové body přímé mříže, plné kroužky pak mřížové body reciproké mříže. Silnou čarou je vyznačena ortogonální centrovaná buňka reciproké mříže o hranách 2a^* a 2b^*.

2. Laueho difrakční podmínky

Nyní potřebujeme zjistit, v jakých směrech dostaneme maxima difraktovaného záření. Uvažujme pružný rozptyl (bez ztráty energie) monochromatického záření o vlnové délce l nejprve na řadě atomů opakujících se s periodou a. Nechť s₀ a s jsou jednotkové vektory ve směru dopadajícího a difraktovaného svazku. Při difrakci rozptylují atomy této řady záření ve fázi a dráhový rozdíl paprsků musí být roven celistvému násobku vlnové délky

as - as₀ = a(s - s₀) = hl .


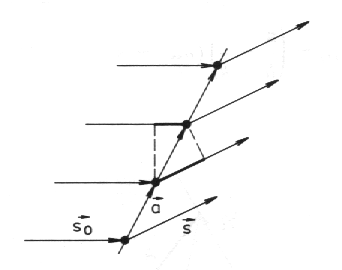Rozptyl na lineární řadě atomů.

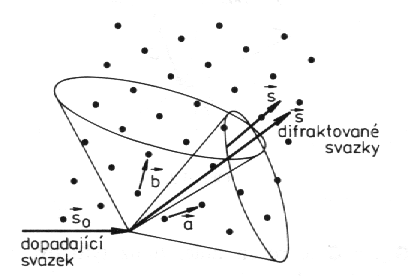
Tato podmínka může být splněna pro celou řadu difraktovaných svazků rozložených na povrchu kužele s osou v atomové řadě. Podobně můžeme pro splnění difrakční podmínky na řadě atomů s periodou b (která svírá nějaký úhel s výše vyšetřovanou řadou) psát

b(s - s₀) = kl ,

kde k je celé číslo. Jsou-li podmínky splněny současně, rozptylují všechny atomy opakující se v rovině s periodami a a b záření ve fázi. Z obrázku je patrné, že podmínky definují dvě kuželové plochy pro dovolené difraktové paprsky. Obě podmínky jsou splněny současně pouze ve dvou difrakčních směrech daných dvěma průniky těchto kuželových ploch. Ve třech rozměrech musí být současně splněny následující tři podmínky

a(s - s₀) = hl ,
b(s - s₀) = kl ,
c(s - s₀) = ll .

Tyto vztahy se nazývají Laueho difrakční podmínky. Vzhledem k tomu, že průnik třetí kuželové plochy s dvěma výše uvažovanými plochami může být pouze podél jedné z přímek s, definují tyto rovnice směr difraktovaného záření jednoznačně.

3. Ewaldova konstrukce

Veličina (s - s₀) / l se nazývá difrakční vektor, jelikož při splnění Laueho podmínek určuje tento vektor směr s difraktovaných svazků při daném směru s₀ dopadajícího záření. Je to veličina definovaná v reciprokém prostoru, neboť má rozměr [m^-1], a může být tudíž vyjádřena vztahem

(s - s₀) / l = pa^* + qb^* + rc^* ,

kde p, q, r jsou zatím neznámé, obecně neceločíselné koeficienty. Při splnění Laueho difrakčních podmínek však musí platit p = h, q = k a r = l (kde h, k, l jsou celá čísla). Laueho difrakční podmínky jsou tudíž splněny tehdy, když je difrakční vektor totožný s nějakým mřížovým vektorem reciproké mříže

(s - s₀) / l = G_hkl .

Tento vztah můžeme vyjádřit graficky pomocí Ewaldovy konstrukce:

  1. Krystal umístíme do středu kulové plochy o poloměru 1/l .
  2. Do bodu 0, kde primární paprsek vychází z této kulové plochy, umístíme počátek reciproké mříže krystalu.
  3. Leží-li nějaký mřížový bod hkl reciproké mříže na této tzv. Ewaldově kulové ploše, jsou splněny Laueho difrakční podmínky pro osnovu rovin ( hkl ) a difraktovaný svazek prochází tímto bodem reciproké mříže (tento bod leží na konci vektoru G_hkl , který je kolmý k rovinám ( hkl )).

Z Ewaldovy konstrukce a Laueho podmínek vyplývá, že difrakční obraz je vlastně zobrazením reciproké mříže krystalu. Tato konstrukce je také vodítkem pro realizaci difrakce monochromatického záření na vybrané osnově rovin. Otáčíme-li krystalem, otáčíme vlastně reciprokou mříží a při známé vlnové délce můžeme z Ewaldovy konstrukce zjistit, ve kterých místech dostaneme difrakční maxima.

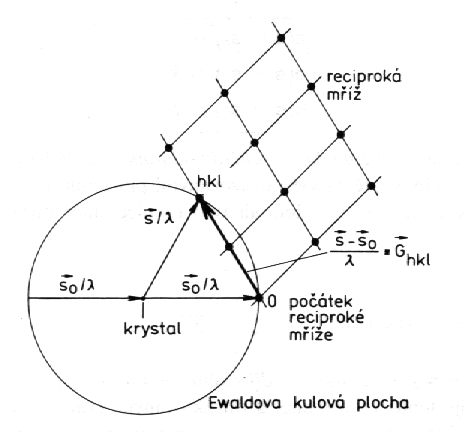Ewaldova konstrukce.

Ewaldova konstrukce demo1, demo2

4. Braggův zákon

Při splnění Laueho difrakčních podmínek, tj. když je difrakční vektor totožný s nějakým vektorem G_hkl reciproké mříže, je tento difrakční vektor kolmý k osnově rovin (hkl) a je půlen rovinou z osnovy (hkl) procházející počátkem přímé mříže krystalu. Svírá-li při splnění Laueho difrakčních podmínek primární svazek s rovinami (hkl) úhel Q, pak stejný úhel Q s nimi svírá i difraktovaný svazek. Situace je tudíž analogická k odrazu (reflexi) paprsku na rovinách (hkl). Proto se často používají termíny "reflexe na rovinách (hkl)" nebo "reflexe hkl", i když se fyzikálně jedná o difrakční proces (ohyb a skládání vln)..

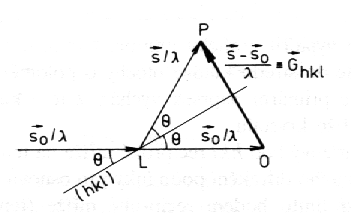K odvození Braggova zákona.

Úhel Q se nazývá Braggův úhel a jeho dvojnásobek 2Q difrakční úhel. (Poznamenejme, že na rozdíl od optiky, kde se úhly dopadu, lomu a odrazu vztahují k normále roviny rozhraní, určuje Braggův úhel odklon paprsků od rovin ( hkl )). Pro Braggův úhel odvodíme z obrázku vztah

sin Q = ( |G_hkl| / 2) / (1/l)

a po dosazení |G_hkl| = 1/d_hkl dostaneme Braggův zákon

2d_hkl sin Q = l .

Indexy hkl vystupující v tomto vytahu určují mřížový bod reciproké mříže, a jsou tedy obecně i soudělná čísla. Nazývají se difrakční indexy (na rozdíl od nesoudělných Millerových indexů). Například difrakci na rovinách (200) můžeme vyjádřit dvojím způsobem:

1. Jako první řád difrakce na rovinách (200), kde 200 jsou difrakční indexy

2d₂₀₀ sin Q₂₀₀ = 1l .

2. Jako druhý řád difrakce na rovinách (100), kde 100 jsou Millerovy indexy

2d₁₀₀ sin Q₂₀₀ = 2l ,

neboť platí d₂₀₀ = d₁₀₀ / 2.

Z Ewaldovy konstrukce a Braggova zákona rovněž dostaneme vztah pro velikost difrakčního vektoru

| (s - s₀) / l | = (2 sin Q) / l .

Poznámka:
Dvě krystalické látky, které mají stejnou krystalovou mříž (a tudíž i stejnou reciprokou mříž), dávají geometricky stejný difrakční obraz, tj. difrakční linie pod stejnými úhly. Například i tak rozdílné látky jako CuJ, MnS₂ a Ag₃AsO₄ se projeví při difrakci geometricky stejně, neboť všechny tři mají mříž se základní buňkou ve tvaru krychle o hraně 6,1.10^-10 m. V prvním případě je v základní buňce umístěno osm atomů dvou druhů, v druhém dvanáct atomů dvou druhů a ve třetím šestnáct atomů tří druhů. Materiální rozdílnost se však projeví v rozdílné intenzitě geometricky identických difrakčních linií.