Dosud diskutované symetrie byly pouze takové, které jsou vlastní mřížím, tedy množinám geometrických (nestrukturních) bodů. Ve skutečných krystalech však může jednotková buňka obsahovat jeden nebo více atomů a uspořádání atomů může mít podstatně nižší symetrii než mříž. Například v triklinické jednotkové buňce může nebo nemusí mít atomové uspořádání střed symetrie. Má-li střed symetrie, je symetrie atomového uspořádání stejná jako symetrie mříže (všechny mříže, a tudíž i triklinická, mají střed symetrie daný již samotnou translační povahou mříže). Nemá-li však uspořádání atomů střed symetrie, nemá krystal žádnou symetrii.
Počet možných symetrických atomových uspořádání je tudíž mnohem větší než počet symetrických prostorových mříží (14 Bravaisových mříží). Některé z možných vnitřních symetrií krystalu se projevují i ve vnějším tvaru a fyzikálních vlastnostech krystalu, jiné však jsou pozorovatelné pouze v atomovém měřítku. Kombinace prvků symetrie pozorovatelné i v makroskopickém měřítku se nazývají bodové grupy. Bodová grupa je skupina prvků symetrie, jejichž operace ponechávají alespoň jeden bod prostoru nepohyblivý.
Symetrie povrchových ploch přirozeně rostlých krystalů (stejně jak symetrie směrů v krystalu) je určena právě jejich bodovou grupou a z hlediska krystalografické systematiky je krystal zařazen do krystalové třídy se stejnou symetrií a symbolem jako odpovídající bodová grupa. Pojmy "krystalová třída" a "bodová grupa" jsou často používána jako synonyma, přesně je však bodová grupa matematický popis a krystalová třída klasifikačním schématem. Název grupa pochází z matematické kategorie grup, neboť operace symetrie mají vlastnosti matematických grup a dají se pomocí teorie grup výstižně formulovat.
Jen pro zajímavost. Matematická grupa je definována takto.
Množina G s prvky a, b, ..., mezi nimiž je definováno násobení, je grupou, pokud platí následující tvrzení:
Tento pojem má velký význam nejen v krystalografii. Pomocí grup však lze dobře formulovat řadu problémů spojených právě se symetrií.
Při odvozování všech možných grup se kombinují různé operace
symetrie. Nejjednodušší je situace v rovině. Grupy obsahují pouze
vlastní osy symetrie 1, 2,
3, 4, 6
a zrcadlení vzhledem k rovině je nahrazeno zrcadlením vzhledem k přímce (m).
Inverzní osy nejsou třeba (![]() a
a
![]() ).
Celkem existuje pouze 10 bodových grup v rovině.
).
Celkem existuje pouze 10 bodových grup v rovině.
Rovinná grupa je grupa operací symetrie, které převádějí dvoudimenzionální objekt v sebe sama. Jejich celkový počet je 17.
13 rovinných grup může být získáno kombinací 10 dvojrozměrných bodových grup s rovinami mříže. 4 další pak nahrazením zrcadlové přímky m skluzovou linií g. Nutno poznamenat, že v symbolice grup nejsou uvedeny všechny obsažené prvky symetrie ale jen ty charakteristické.
17 možných rovinných grup:
| Rovnoběžníková | p1 | p2 | ||
| Pravoúhlá | pm | pg | cm | p2mm |
| p2mg | p2gg | c2mm | ||
| Čtvercová | p4 | p4mm | p4gm | |
| Trojúhelníková | p3 | p3m1 | p31m | |
| p6 | p6mm |
Po kliknutí na příslušný symbol grupy se otevře nové okno, kde se objeví základní buňka s vyznačeným rozmístěním prvků symetrie (osy pomocí konvenčních symbolů, zrcadlové roviny m (_______) a skluzové roviny g (_ _ _ _ _ _)). Po kliknutí na Demo se otevře program, který pro danou grupu umožňuje nakreslit nějaký vzor a sledovat, co s ním udělají operace symetrie (předposledním tlačítkem shora), tedy jak ho zmnoží.
Pro podobný účel slouží aplet S. Webera
Bodových grup je celkem 32 a můžeme je podle společné hlavní osy nebo společných osových kombinací rozdělit do 7 krystalových soustav. Kritériem pro zařazení krystalu do některé soustavy je určitá minimální symetrie.
| Soustava | Schoenfliesův symbol | Mezinárodní symbol | p |
| triklinická | C1 | 1 | 1 |
| Ci | 1i | 2 | |
| monoklinická | C2 | 2 | 2 |
| C1h | m | 2 | |
| C2h | 2/m | 4 | |
| ortorombická | D2 | 222 | 4 |
| C2v | mm2 | 4 | |
| D2h | 2/m 2/m 2/m = mmm | 8 | |
| tetragonální | C4 | 4 | 4 |
| S4 | 4i | 4 | |
| C4h | 4/m | 8 | |
| D4 | 422 | 8 | |
| C4v | 4mm | 8 | |
| D2d | 4i2m | 8 | |
| D4h | 4/m 2/m 2/m = 4/mmm | 16 | |
| trigonální | C3 | 3 | 3 |
| C3i | 3i | 6 | |
| D3 | 32 | 6 | |
| C3v | 3m | 6 | |
| D3d | 3i 2/m = 3im | 12 | |
| hexagonální | C6 | 6 | 6 |
| C3h | 6i | 6 | |
| C6h | 6/m | 12 | |
| D6 | 622 | 12 | |
| C6v | 6mm | 12 | |
| D3h | 6im2 | 12 | |
| D6h | 6/m 2/m 2/m = 6/mmm | 24 | |
| kubická | T | 23 | 12 |
| Th | 2/m 3i = m3i | 24 | |
| O | 432 | 24 | |
| Td | 4i3m | 24 | |
| Oh | 4/m 3i 2/m = m3im | 48 |
V tabulce jsou animované obrázky znázorňující zmnožení
motivu a prvky symetrie v jednotlivých grupách.
Schoenfliesova symbolika souvisí úzce s odvozením všech bodových grup a
nebudeme se jí zde zabývat, např. Cn značí grupu obsahující
pouze n-četnou osu, Cnv obsahuje vertikální polární n-četnou
osu a n rovin zrcadlení procházející podél ní (vertikální
roviny),C nhobsahuje kromě vertikální n-četné osy
ještě kolmou rovinu zrcadlení (horizontální rovina),
Mezinárodní (Hermannovy-Mauguinovy)
symboly bodových grup se skládají ze symbolů prvků symetrie ve význačných
směrech. Pro jednotlivé soustavy jsou to směry:
| 1) triklinická | |
| - nemá význačný směr, | |
| 2) monoklinická | |
| - význačným směrem je směr osy 2 nebo 2i, který volíme podél souřadné osy y nebo z, | |
| 3) ortorombická | |
| - má 3 význačné směry podél navzájem kolmých souřadných os x, y, z, | |
| 4) trigonální, tetragonální, hexagonální | ||||||||||
| - mají 3 význačné směry: | ||||||||||
|
||||||||||
| 5) kubická | ||||||||||
| - má 3 význačné směry: | ||||||||||
|
||||||||||
Například bodová grupa mm2 ortorombické soustavy má roviny m kolmé k osám x a y a osu 2 rovnoběžnou s osou z. Nebo bodová grupa 4i2m tetragonální soustavy má osu 4i podél osy z, osu 2 podél osy y a rovinu m kolmou k úhlopříčce mezi souřadnými osami x a y.
Tabulka také obsahuje počet ekvivalentních bodů p, které
vzniknou z jednoho bodu v obecné poloze všemi operacemi bodové grupy.
Obecná poloha je taková, ve které neleží žádný prvek symetrie. To znamená,
že je maximálně zmnožen operacemi symetrie grupy (žádná ho nenechá
netknutým)
Například 4četná osa vytvoří čtyřmi operacemi z jednoho bodu čtyři body, rovina zrcadlení a střed symetrie dva body atd. Počet ekvivalentních bodů je tedy současně roven počtu operací symetrie bodové grupy.
Prostorové grupy jsou zvláště důležité pro popis krystalových struktur. Text není zcela nutný k vypracování úkolu 3. lekce, ale přesto doporučujeme ho přečíst.
Z předchozího je zřejmé, že ke každé bodové grupě (projevující se ve vnějším tvaru krystalu) existuje obecně několik možných prostorových vzorů. Symetrie těchto vzorů mohou být nalezeny postupným nahrazováním souborů čistých os otáčení v bodové grupě vhodnými šroubovými osami s různými translačními složkami a nahrazováním rovin zrcadlení skluzovými rovinami. Tyto nové soubory prvků symetrie se nazývají prostorové grupy. Zachovávají úhlové vztahy výchozí bodové grupy a říkáme, že jsou izogonální s určitou bodovou grupou.
Prostorových grup je celkem 230.
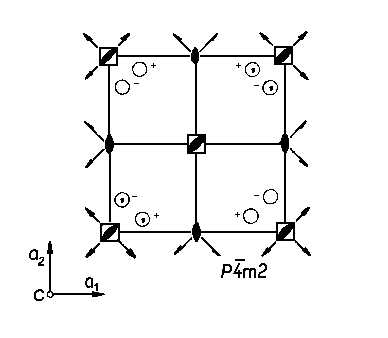
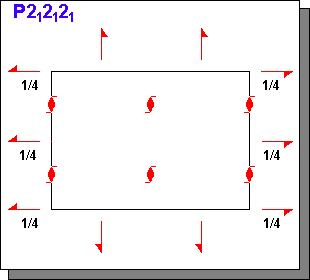
Symboly prostorových grup. Úplný symbol prostorové grupy sestává ze čtyř znaků. První je písmeno označující typ mříže. Za ním následuje trojice symbolů označujících prvky symetrie, které byly kombinovány s translacemi mříže při vytváření prostorové grupy. Pořadí těchto symbolů se vztahuje k význačným směrům v dané soustavě (viz předchozí část věnovanou bodovým grupám). Např. u prostorové grupy P63mc hexagonální soustavy míří šroubová osa 63 podél I. význačného směru, tj. podél osy c, roviny m jsou kolmé k II. význačnému směru, tj. kolmé k osám a1 a a2 a skluzová rovina c je kolmá ke III. význačnému směru, tj. ke směru [120]. Symbol bodové grupy se odvodí ze symbolu prostorové grupy tak, že se myšlenkově zanedbají subtranslace šroubových os a skluzových rovin. V uvedeném příkladu dostaneme podle tohoto schématu 6 místo 63, m místo c a symbol bodové grupy je 6mm. Pomocí symbolu bodové grupy určíme krystalovou soustavu, v našem případě hexagonální. Prostorová grupa tudíž obsahuje veškeré informace o symetrii krystalu, ať se již jedná o symetrii atomové struktury nebo o makroskopickou symetrii krystalu. Počet a druh operací symetrie prostorové grupy je však obecně větší, než udává symbol prostorové grupy. Úplné soubory operací symetrie prostorových grup a jejich rozmístění v základní buňce jsou uvedeny v Mezinárodních krystalografických tabulkách. Jako příklady jsou na obrázku graficky znázorněny grupy P4im2 (i značí inverzní osu pro potřeby tohoto textu) tetragonální soustavy a P212121, kde jsou nakresleny v příslušných polohách jednotlivé prvky symetrie.