KRYSTAL JAKO TROJROZMĚRNĚ PERIODICKÝ VZOR

Pro popis struktury a symetrie krystalů je užitečné zavést pojem ideálního krystalu. Ideální krystal je nekonečný a jeho struktura je zcela pravidelná. Tím, že jej považujeme za nekonečný, vlastně zanedbáváme povrch krystalu, tedy všechny atomy pokládáme za vnitřní. Že naše úvaha má smysl dokazuje např. krychlička hliníku o hraně 1 nm (zhruba velikost nejjemnějších krystalových zrn v technických kovech) - poměr vnitřních a vnějších atomů činí asi 800.

Základním rysem pravidelnosti ideálních krystalů je jejich trojrozměrná translační periodicita - projevuje se pravidelným opakováním základního motivu (hmotné báze) tvořeného jedním nebo více atomy ve třech rozměrech. Vzhledem k tomu, že počet atomů tvořících základní motiv může být značně velký (až tisíce atomů u organických krystalů), je z hlediska dalších úvah užitečné představovat si základní motiv tvořený spíše více atomy a obecného tvaru. A jelikož asymetrické tvary mohou nabývat dvou nezaměnitelných podob, pravé a levé, je třeba respektovat i tuto skutečnost hned v úvodu (přesvědčivým příkladem nezaměnitelnosti pravých a levých objektů je "pravá a levá bota"). Při úvahách o symetrii krystalů je konečně rozumné pracovat s obecným trojrozměrným vzorem namísto s konkrétními typy atomových struktur.

Pravidelný trojrozměrný vzor lze vytvořit ze základního motivu operacemi opakování: translací (tj. posunutím), otáčením (a), zrcadlením (b), inverzí (tj. středovou souměrností - c) nebo operacemi složenými z těchto operací. Na obrázku jsou znázorněny uvedené operace opakování a všimněte si, že zrcadlení a inverze převádí pravé objekty v levé (a naopak), zatímco translací a otočením se podoba objektu nemění. Všechny pravé objekty jsou shodné, (a rovněž tak i všechny levé objekty mezi sebou), zatímco pravé a levé objekty jsou vůči sobě protitvaré, enantiomorfní. Je zřejmé, že inverzi lze složit ze zrcadlení a otáčení anebo naopak vytvořit zrcadlení pomocí inverze a otáčení. Stačilo by tedy omezit se na tři základní operace, např. translaci, otáčení a zrcadlení.

Pravidelný vzor vytvořený těmito operacemi opakování je pak symetrický, tj. přechází sám v sebe operacemi symetrie. Prvek symetrie je množina bodů, které se při operaci symetrie nepohybují. Takovými prvky symetrie jsou např. n-četná osa otáčení (označení n), rovina zrcadlení (označení m z angl. "mirror" - zrcadlo) nebo střed symetrie (označení i od "inverze" nebo "1 s pruhem"). Tyto pojmy budou názorně vysvětleny v další lekci.

Translační periodicita mříží

Zajímáme-li se spíše o geometrii vzoru vzniklého translačním opakováním - posouváním - ve třech rozměrech než o detaily opakovaného motivu, může být vzor představen body, které se opakují ve třech směrech s periodami t₁, t₂ a t₃. Na obrázku je - a) nesymetrický vzor vytvořený translacemi t₁, t₂ a t₃  ve třech směrech, b) trojrozměrná mříž vzoru.

Takováto trojrozměrně periodická množina bodů se nazývá prostorová mříž. Mříž je geometrické místo bodů, které mají stejné a stejně orientované okolí. Z této definice vyplývá, že volba počátku mříže je libovolná. Tuto skutečnost je třeba zdůraznit, neboť často bývá nesprávně mříž pokládána za množinu bodů odpovídajících středům všech atomů v dané struktuře. Mřížové body ale nemusí být totožné se středy atomů, mohou být i mezi nimi. Na dvourozměrném příkladu je znázorněn vzor vzniklý opakováním motivu tvořeného dvěma různými (nestejně velkými) atomy. Jednou je počátek mříže zvolen ve středu spojnice atomů, podruhé ve středu většího atomu. Tečky vyznačující mřížové body vytvářejí v obou případech stejnou rovinnou mříž.  

Pozornost zasluhuje i rozlišování pojmů struktura a mříž. Strukturou krystalu rozumíme prostorové uspořádání atomů, zatímco mříž vystihuje pouze translační periodicitu tohoto uspořádání, jakýsi "věšák", v jehož rámci můžeme strukturu popsat, například pomocí umístění atomů v jedné buňce mříže.

Základní buňka

Mříž může být reprezentována trojicí vektorů (veličin, které mají velikost a také směr) t₁, t₂ a t₃, zvolených tak, že libovolnému mřížovému bodu odpovídá vektor

T = ut1 + vt2 + wt3 ,

a   u,v,w jsou celá čísla. Jsou-li vybrány vektory t₁, t₂ a t₃, je mříž jednoznačně definována tímto vztahem. Naopak však daná mříž neurčuje jedinou trojici základních translací, jak je vidět ve dvojrozměrném případě, kde translace t₂ i t´₂ opakují řadu mřížových bodů se separací t₁ ve druhém rozměru se stejným výsledkem. Vidíme tedy, že základní vektory lze volit různým způsobem. Nejvhodnější je ale takový, kdy vektory jsou krátké, pokud je to možné na sebe kolmé a také vyjadřující symetrii mříže. Vektory jsou veličiny, u kterých je důležitý směr a velikost. Můžeme si je značit úsečkami zakončenými šipkou. Není důležitý počátek. Můžeme je tedy libovolně posouvat tak, aby zůstaly rovnoběžné s původním směrem.

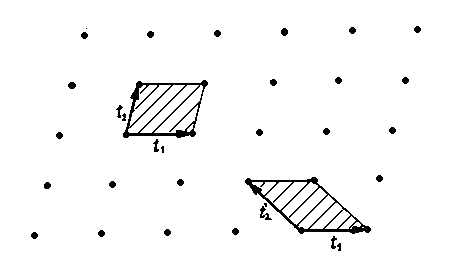
 V podstatě můžeme zvolit základní translace dvojím způsobem:

   (a) Obsahuje-li rovnoběžnostěn vymezený základními translacemi  (vyšrafovaný na obrázku) pouze jediný mřížový bod, je tento rovnoběžnostěn nazýván primitivní buňka. Tak tomu je na obrázku. Z každého bodu padne do rovnoběžnostěnu čtvrtina. Tedy celkem jeden bod.

   (b) Obsahuje-li rovnoběžnostěn vymezený základními translacemi více mřížových bodů, je tento rovnoběžnostěn nazýván centrovaná buňka. To bychom si mohli představit, pokud by na obrázku byl uvnitř rovnoběžnostěnu ještě jeden bod.

Lze snadno dokázat, že všechny primitivní buňky mají stejný objem a že tento objem je minimální, jaký může buňka mříže mít. Rovněž tak je zřejmé, že centrované buňky mají objem rovný celistvému násobku objemu primitivní buňky (podle počtu mřížových bodů připadajících na centrovanou buňku).

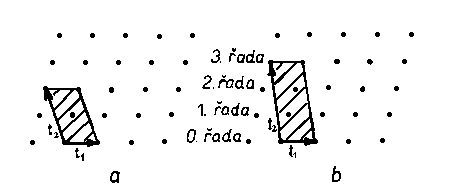Primitivní buňka	Centrované buňky

Je tudíž zřejmé, že o typu základní buňky rozhoduje počet mřížových bodů připadajících na buňku a nikoliv počet atomů. Zavedení centrovaných buněk je dáno požadavkem, aby symetrie základní buňky byla stejná jako symetrie celé mříže. Translace vymezující zvolenou základní buňku se nazývají krystalografické osy a označují se konvenčně jako vektory a, b, c - s pravotočivým sledem. Délky hran základní buňky (tj. délky krystalografických os) a úhly mezi nimi vytvářejí soubor mřížových parametrů. Mříže s centrovanou buňkou se nazývají centrované mříže. 

Značení mřížových rovin a směrů

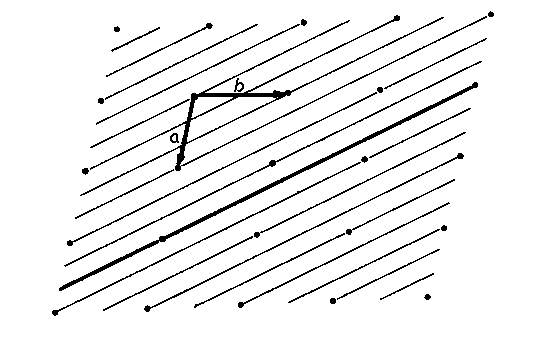
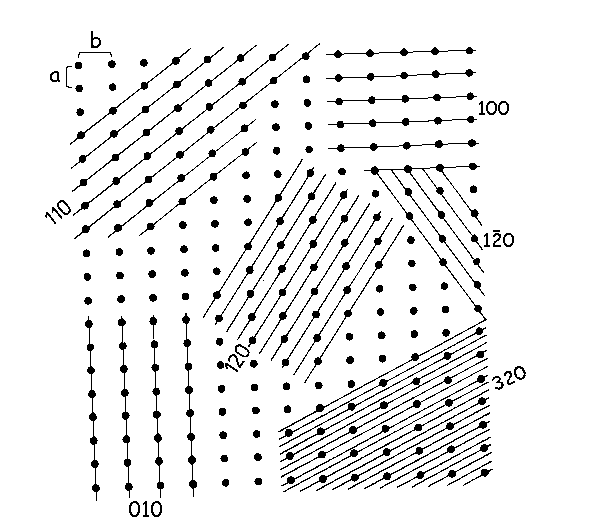
Rovina procházející třemi mřížovými body, které neleží na přímce, se nazývá mřížová rovina. Ke každé mřížové rovině existuje celá posloupnost mřížových rovin, nazvaná osnova mřížových rovin. Mezirovinná vzdálenost d, tj. vzdálenost dvou sousedních rovin jedné osnovy, je konstantní a charakteristická pro danou osnovu mřížových rovin. Orientaci mřížové roviny (a tudíž i orientaci celé osnovy mřížových rovin) vůči krystalografickým osám popisují Millerovy indexy h, k, l. Jsou to celá nesoudělná čísla, udávající, na kolik dílů dělí daná osnova rovin krystalografické osy a, b, c. Dělí-li např. nějaká osnova rovin osu a na 3 díly, osu b na 2 díly a s osou c je rovnoběžná, je Millerův symbol této osnovy (320).

Millerovy indexy můžeme také určit z úseků které vytíná na osách a, b, c rovina osnovy ležící nejblíže počátku (neprocházející však počátkem). Millerovy indexy jsou pak rovny převráceným hodnotám úseků vyťatých touto rovinou na krystalografických osách. V uvedeném příkladu protíná tato rovina osu a v 1/3 její délky, osu b v 1/2 a osu c v nekonečnu. Převrácené hodnoty dávají opět indexy 3, 2, 0. Millerovy indexy určují nejen orientaci osnovy rovin v krystalu, ale i mezirovinnou vzdálenost v této osnově rovin. Například pro krystaly kubické soustavy platí

Skupina symetricky ekvivalentních mřížových rovin se nazývá forma, značí se symbolem {hkl} a počet rovin v této skupině nazýváme četnost. Symetricky ekvivalentní roviny např. v krychli jsou všechny stěny. Z hlediska symetrie je od sebe nerozeznáme.