PRVKY SYMETRIE


Nejen pro klasifikaci krystalových struktur ale i pro jejich určování má zásadní význam určit jaké prvky symetrie existují pro různé typy struktur.

Pokud objekt zůstane po provedení operací symetrie nezměněn, říkáme, že má symetrii a operace se nazývají operacemi symetrie.

Prvky symetrie jsou body, osy a roviny, vzhledem k nimž jsou operace prováděny.

Rotační osy symetrie

Pokud všechny vlastnosti objektu zůstávají nezměněny po rotaci o    kolem osy, je tato osa osou symetrie četnosti n.

V ilustracích je uvedena trojdimenzionální demonstrace symetricky ekvivalentních bodů a také projekce užívající mezinárodních symbolů. Objekt je reprezentován symbolem , znaménko + značí, že je objekt před obrazovkou a - naopak za obrazovkou. V animacích je objekt prezentován zelenou kuličkou. Animaci lze spustit tlačítkem Play a nebo po krocích Step.

Jednočetná osa
Triviální osa. Nazývá se identita. Objekt zůstavá nezměněn po rotaci o  kolem jakékoli osy procházející jakýmkoli bodem. Neexistují žádné symetricky ekvivalentní body.

Dvojčetná osa
značí se symbolem pokud je osa kolmá k obrazovce a pokud je rovnoběžná s obrazovkou. Objekt zůstává nezměněn po rotaci o  kolem osy. Existují dva ekvivalentní objekty, které jsou spojeny rotací o .

Trojčetná osa
značí se symbolem  pokud je osa kolmá k obrazovce a   pokud je rovnoběžná s obrazovkou. Objekt zůstává nezměněn po rotaci o kolem osy. Existují tři ekvivalentní objekty, které jsou spojeny rotací o .

Čtyřčetná osa
značí se symbolem pokud je osa kolmá k obrazovce a pokud je rovnoběžná s obrazovkou. Objekt zůstává nezměněn po rotaci o   kolem osy. Existují čtyři ekvivalentní objekty, které jsou spojeny rotací o .

Pětičetná osa
značí se symbolem pokud je osa kolmá k obrazovce a pokud je rovnoběžná s obrazovkou. Objekt zůstává nezměněn po rotaci o    kolem osy. Existuje pět ekvivalentních objektů, které jsou spojeny rotací o .

Šestičetná osa
značí se symbolem pokud je osa kolmá k obrazovce a pokud je rovnoběžná s obrazovkou. Objekt zůstává nezměněn po rotaci o  kolem osy. Existuje šest ekvivalentních objektů, které jsou spojeny rotací o .

A podobně můžeme pokračovat dál.

Prvek symetrie přítomný v krystalu musí vyhovovat symetrickému uspořádání mřížových bodů, které je dáno translační periodicitou mříže a naopak prvek symetrie krystalu určuje, jaký druh mříže může tento krystal mít. Má-li být například prvkem symetrie rotační osa, musí být mříž symetrická vůči otáčení kolem nějaké osy A o úhel a a jeho celistvé násobky. Kdybychom tuto operaci prováděli opakovaně, pak se mříž po n otočeních dostane do výchozí polohy, neboli platí

 na= 2p.

Naskýtá se otázka, jakých četností mohou rotační osy nabývat u trojrozměrně periodických vzorů, tj. i u ideálních krystalů. Již rovinné mříže určují tato omezení četnosti rotačních os, neboť prostorové mříže vznikají z rovinných jejich vrstvením.

Lze ukázat, že pětičetná osa a osy s četností větší než 6 nejsou slučitelné s translační periodicitou mříže. Je však třeba poznamenat, že i tyto "zakázané" osy se mohou v krystalech vyskytovat jako prvky symetrie celé struktury ideálních krystalů. Rovněž tak se mohou vyskytovat u přírodních objektů, jako jsou např. květiny, u kterých odpadá omezení dané u krystalů jejich translační periodicitou.

Inverzní osy symetrie

Inverzní osy jsou složené prvky symetrie, jejichž operace symetrie sestává z otáčení a inverze. Nezáleží na pořadí těchto operací, tato složená operace se však opakuje jako celek, tj. nelze například provést řadu otáčení a po nich inverzi (nebo řadu inverzí). Objekt má inverzní osu symetrie četnosti n pokud zůstane nezměněn po rotaci o kolem osy symetrie a následné inverzi vzhledem k bodu na této ose. Užívaný symbol je . 

Trojčetná inverzní osa např. opakuje výchozí bod následujícím způsobem: první operace této osy otočí bod o 120° a vytvoří jeho středově symetrický obraz; tento obraz se stane výchozím bodem pro druhou operaci 3četné inverzní osy, která ho opět otočí o 120° a středově symetricky zobrazí atd. Dva objekty spojené touto osou jsou enantiomorfní; tzn. jestliže jeden je reprezentován symbolem , druhý symbolem . Převádějí se tedy levé objekty na pravé a naopak.

Jednočetná inverzní osa
 grafický symbol . Triviální osa je shodná s inverzí vzhledem ke středu symetrie. Existují dva ekvivalentní objekty.

Dvojčetná inverzní osa  
grafický symbol pokud je osa kolmá k obrazovce, pokud je rovnoběžná. Symetricky ekvivalentní bod se získá po rotaci o    kolem osy následované inverzí vzhledem bodu na této ose. je ekvivalentní zrcadlení podle roviny kolmé k ose. Existují dva ekvivalentní objekty.

Trojčetná inverzní osa
grafický symbol  pokud je osa kolmá k obrazovce, pokud je rovnoběžná. Symetricky ekvivalentní bod se získá po rotaci o   kolem osy následované inverzí vzhledem bodu na této ose. je ekvivalentní kombinaci 3 a . Tedy = 3.

Čtyřčetná inverzní osa
grafický symbol pokud je osa kolmá k obrazovcen, pokud je rovnoběžná. Symetricky ekvivalentní bod se získá po rotaci o    kolem osy následované inverzí vzhledem bodu na této ose.  je také dvojčetnou osou.

Šestičetná inverzní osa
grafický symbol pokud je osa kolmá k obrazovce, pokud je rovnoběžná. Symetricky ekvivalentní bod se získá po rotaci o    kolem osy následované inverzí vzhledem bodu na této ose.   je ekvivalentní kombinaci trojčetné osy a zrcadlení přes kolmou rovinu: = 3/m.

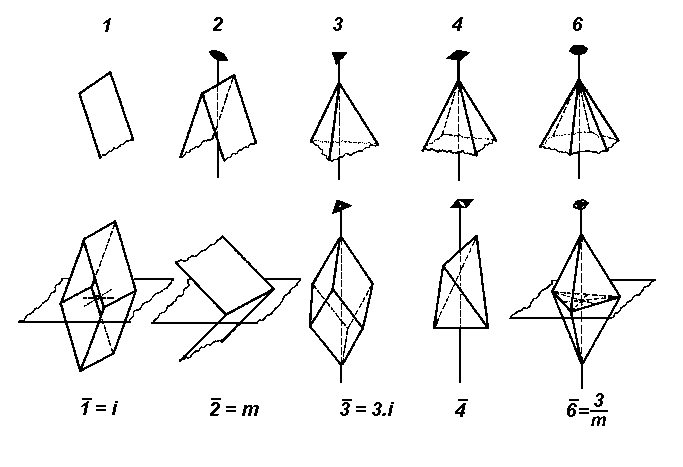
Inverzní osy se také označují jako nevlastní osy. Na obrázku je znázorněno opakování roviny vlastními a nevlastními osami otáčení. Útvary omezené těmito rovinami mají symetrii odpovídajících os v naznačených směrech a mohou se projevit v morfologii krystalu.

 
obr4-4.gif

 

Další prvky symetrie vzniknou kombinací již uvedených s translací. Jsou to šroubové osy a skluzové roviny.

 

Další text není nutný k vypracování úloh.

Šroubové osy

Šroubová osa symetrie četnosti n je přítomna, pokud všechny vlastnosti prostoru zůstanou nezměněny po rotaci o kolem osy a translaci t podél této osy. Dále budeme uvažovat omezení daná translační periodicitou krystalů (mříže) T. Pokud aplikujeme operaci otočení kolem osy n krát, celkové otočení bude   a celková translace nt . Pro zachování periodicity krystalu musí platit

nt = pT, kde p je celé číslo

Například pro čtyřčetnou šroubovou osu jsou povolené translace (0/4)T , (1/4)T , (2/4)T , (3/4)T , (4/4)T. Tedy p může být pouze z intervalu (0 , n). Šroubovou osu zcela charakterizuje symbol np kde n je četnost a p/n definuje translační část. Možné osy symetrie včetně šroubových tedy jsou:

2 , 21
3 , 31 , 32
4 , 41 , 42 , 43
6 , 61 , 62 , 63 , 64 , 65

 resp s jejich symboly a naznačeným opakováním objektu.
Skládání otáčení s kolmou složkou translace vede pouze k opakovanému výskytu výchozí rotační osy (důkaz)

Skluzové roviny

Skluzová rovina je spojení zrcadlení s následnou translací rovnoběžnou s rovinou zrcadlení. Uvažujme opět omezení dané translační periodicitou. Nechť  t je skluzový vektor a T periodicita mříže ve směru skluzu. Opakujeme-li operaci skluzu dvakrát, bude výsledná translace 2t. Pro zachování translační periodicity musí platit

2 t = p T , kde p je celé

Dostaneme tak následující translace: 0 T, (1/2) T, T, (3/2) T, .....z nichž pouze první dvě jsou různé. Pro p = 0 dostaneme čistou rovinu zrcadlení m. 

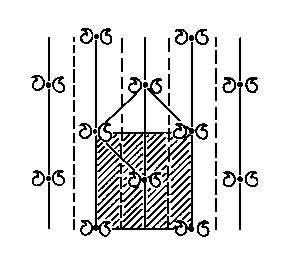Existenci skluzových rovin jako skutečných prvků symetrie periodických vzorů (a tudíž i ideálních krystalů) můžeme nahlédnout z dvojrozměrného příkladu na obrázku. V tomto rovinném vzoru je na první pohled zřejmá přítomnost rovin zrcadlení kolmých k nákresně; jejich stopa je obrázku znázorněna plnou čarou. Tento rovinný vzor však přechází sám v sebe i operacemi složenými ze zrcadlení vůči rovinám vyznačeným čárkovaně a z translace , jejíž délka je rovna jedné polovině hrany čtvercové buňky (vyznačené šrafovaně). Uvažovaná buňka je centrovaná a tato skutečnost již naznačuje, že translační složky skluzových rovin bodou spojeny se subtranslacemi centrovaných mříží. Translační složka t je rovna jedné polovině mřížové translace ve směru skluzu. Skluz podél osy a má tudíž t = (1/2)t a nazývá se a-skluz. 

 

 

Dále jen pro úplnost.

Úhlopříčný skluz má translační složky t = (1/2)a + (1/2)b nebo (1/2)b + (1/2)c, atd. Možné skluzové roviny a jejich translační složky jsou uvedeny v tab. 5.2. Translační složka t u diamantového skluzu je ve skutečnosti rovna jedné polovině mřížové subtranslace podél stěnové úhlopříčky plošně centrované buňky.

 

Skluzové roviny
Typ skluzu Symbol Orientace skluzové roviny Translační složky t
osový a ^b nebo ^c 1/2a
osový b ^c nebo ^a 1/2b
osový c ^a nebo ^b 1/2c
úhlopříčný n ^c; ^a; ^b 1/2(a+b); 1/2(b+c);
1/2(a+c)
diamantový d ^c; ^a; ^b 1/4(a±b); 1/4(b±c);
1/4(a±c)

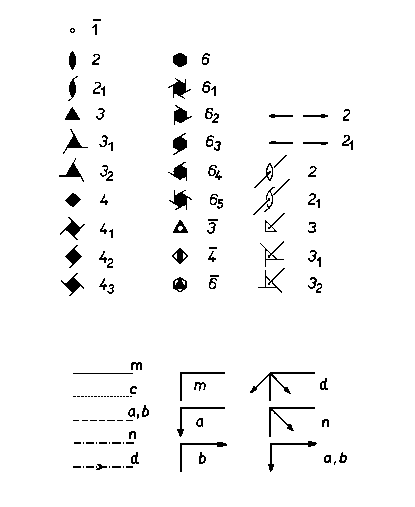Na dalším obrázku jsou souhrnně uvedeny symboly všech krystalografických prvků symetrie, které se konvenčně používají k vyznačení poloh prvků symetrie v základní buňce. V levé části obrázku jsou uvedeny symboly prvků symetri orientovaných kolmo k nákresně, v pravé části pak symboly vybraných rotačních os a všech skluzových rovin (včetně zrcadlové roviny s nulovým skluzem) používané pro tyto prvky orientované rovnoběžně s nákresnou nebo šikmo k nákresně (u os 2, 21, 3, 31, 32).