Osy symetrie

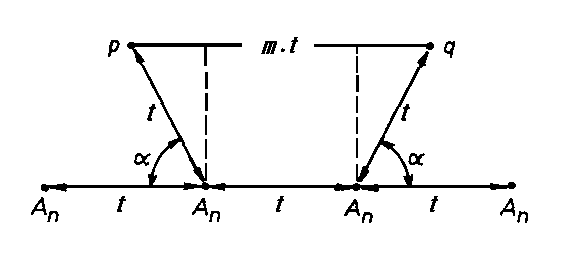
Ve spodní části obrázku je znázorněna řada mřížových bodů nějaké rovinné mříže, vzdálených o délku t translační periody. Uvažujme obecnou n-četnou osu An umístěnou v každém mřížovém bodě kolmo k nákresně. Osy An procházející dvěma prostředními mřížovými body opakují translace t po a stupních (a=2p/n) na obě strany. Má-li být rovinná mříž symetrická vůči těmto osám An, musí se mřížové body vyskytovat i na koncích pootočených translací t. Mřížové body p a q, které takto vzniknou, jsou stejně vzdáleny od základní mřížové řady a leží v nelbližší řadě mřížových bodů. Translační periodita rovinné mříže však vyžaduje, aby jejich vzdálenost byla celistvým násobkem periody t. Možné hodnoty úhlu a lze tak určit z geometrické podmínky

mt = t + 2tcos a,

m = 0, ±1, ±2, ±3, ....,

cos a = (m-1)/2.

Jelikož hodnota |cos a| může být pouze menší nebo rovna jedné, dostáváme pro m-1 od -2 do +2 pět hodnot dovolených úhlů a, a tudíž i pět dovolených četností rotačních os konzistentních s translační periodicitou mříže

Určení možných četností rotačních os v ideálních krystalech
m - 1	cos a	a ( ° )	n
-2 -1 0 +1 +2	-1 -1/2 0 +1/2 +1	180 120 90 60 0 nebo 360	2 3 4 6 1

Z uvedeného je patrné, že pětičetná osa a osy s četností větší než 6 nejsou slučitelné s translační periodicitou mříže. Je však třeba poznamenat, že i tyto "zakázané" osy se mohou v krystalech vyskytovat jako prvky symetrie celé struktury ideálních krystalů. Rovněž tak se mohou vyskytovat u přírodních objektů, jako jsou např. květiny, u kterých odpadá omezení dané u krystalů jejich translační periodicitou.