Fourierova transformace

Difrakci lze v určitém přiblížení chápat také jako tzv. Fourierovu transformaci objektu. To je matematická transformace, která se často ve fyzice, ale i dalších oborech používá.
Pomocí následujících apletů je možné generovat motivy a zobrazovat jejich Fourierovy transformace, tedy difrakční obrazy.

Pomocí těchto apletů byly generovány následující ilustrační příklady. Podívejte se nejprve na ně.
V tabulkách jsou ilustrovány obecné a speciální polohy a vlastnosti Fourierovy transformace. Jsou také vždy ukázány obrazy.
Vidíte, že někdy obrazy vypadají podobně i pro různé buňky.

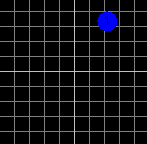
Základní buňka	Mříž	Příslušná Fourierova transformace

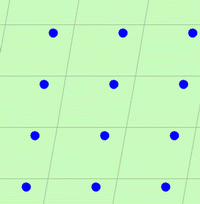
Atom v obecné poloze	Grupa p1 – není žádná symetrie. Atom není zmnožen. V každé buňce je jeden.

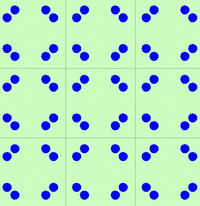
Atom v obecné poloze	Grupa p4 – čtyřčetná symetrie. Atom v obecné poloze je zmnožen.	Čtyřčetná symetrie je viditelná i v tomto obraze.

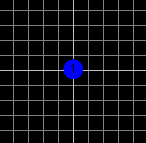
Atom ve speciální poloze na čtyřčetné ose.	Grupa p4 – čtyřčetná symetrie. Atom ve speciální poloze (na ose) není zmnožen.

Atom v obecné poloze	Grupa pg – skluzová rovina.

Atom v obecné poloze	Grupa p4mm – čtyřčetná osa, dvě kolmé roviny zrcadlení. Atom v obecné poloze je několikrát zmnožen.

Atom v obecné poloze	Grupa p3m1 – trojčetná osa, rovina zrcadlení.

Atom v obecné poloze	Grupa p6 – šestičetná osa

Atom v obecné poloze	Grupa p6mm – šestičetná osa, roviny zrcadlení