XRDMLread Examples
In this section you can find few demonstrations how to load and process data by the XRDMLread.
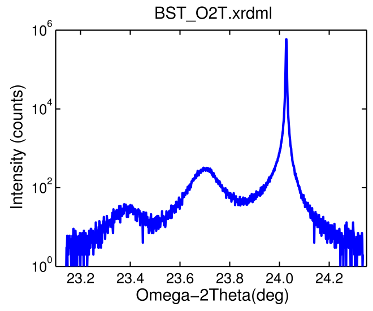
- Example no. 1 is a simple demonstration how to load a single scan using the XRDMLread function.
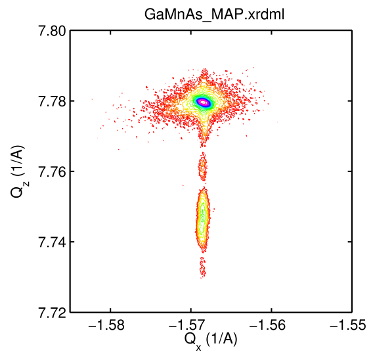
- Example no. 2 demonstrates visualisation of a two axes measurement data.
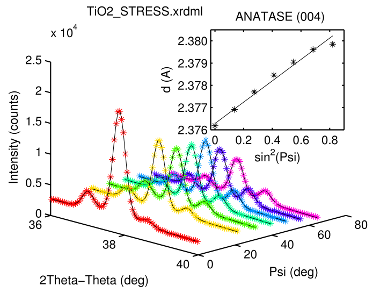
- Example no. 3 shows an application of the Sin2(Psi) method to three simultaneously measured neighbouring anatase lines of a Ti02 thin film sample.
Example no. 1
is a simple demonstration how to load a single scan using the XRDMLread function.
% load XRDML data by a simple single command d = XRDMLread('BST_O2T.xrdml') %#ok<NOPTS> % plot data figure semilogy( d.x , round(d.data*d.time) ) box on xlabel( [d.xlabel '(' d.xunit ')'] ) ylabel( 'Intensity (counts)' ) title( d.filename , 'Interpreter','none','FontName','Helvetica')
Download
- example1.m (src)
- BST_O2T.xrdml (data)
Example no. 2
demonstrates visualisation of a two axes measurement data.
d = XRDMLread('GaMnAs_MAP.xrdml') %#ok<NOPTS> figure % create an appropriate log scale v = logspace( mean(d.data(d.data<5)) , log10(max(max(d.data))) , 21 ); col = hsv(21); % calculate the contour matrix C = contourc( d.Theta2(1,:) , d.Omega(:,1)-d.Theta2(:,1)/2 , ... d.data , v ); % transform contours coordinates into the Q-space % and draw them H = []; nn = 0; hold on while nn+1<size(C,2) % extract data value = C(1,nn+1); level = find(v == value); dim = C(2,nn+1); ind = nn+1+(1:dim); x = C(1,ind); y = C(2,ind); % transformation Qx = 2*pi/d.Lambda*(-cos((x/2-y)*pi/180) + cos((x/2+y)*pi/180) ); Qz = 2*pi/d.Lambda*( sin((x/2-y)*pi/180) + sin((x/2+y)*pi/180) ); % draw line H(end+1) = line(Qx,Qz,'Color',col(level,:)); %#ok<SAGROW> % draw patch (Matlab) %H(end+1) = patch(Qx,Qz,col(level,:),'Line','none'); %#ok<SAGROW> % save data C(1,ind) = Qx; C(2,ind) = Qz; % increase index nn = nn+dim+1; end axis square box on xlabel('Q_x (1/A)') ylabel('Q_z (1/A)') title( d.filename ,'Interpreter','none','FontName','Helvetica')
Download
- example2.m (src)
- GaMnAs_MAP.xrdml (data)
Comment: In this example instead of a calculation of the contour plot in the non-equidistant Q-space points
the contours are rather calculated in the grid of measured points and then the transformed coordinates of the
equi-intensity lines are plotted manually.
Example no. 3
shows an application of the Sin2(Psi) method to three simultaneously measured neighbouring anatase lines of a Ti02 thin film sample.
d = XRDMLread('TiO2_STRESS.xrdml'); figure hold on col = hsv(length(d.Psi)); for k=1:length(d.Psi) plot3( d.Theta2(k,:) , repmat(d.Psi(k),1,size(d.data,2)) , ... round(d.data(k,:)*d.time), '*' , 'Color' , col(k,:) ) end view(45,20) xlabel( [d.xlabel ' (' d.xunit ')'] ) ylabel( [d.ylabel ' (' d.yunit ')'] ) zlabel( 'Intensity (counts)' ) title( d.filename , 'Interpreter','none','Interpreter','none','FontName','Helvetica') % set global wavelength data for the pseudoVoigt function global WAVELENGTHS switch d.kType case {'K-Alpha 1'} WAVELENGTHS = [1.0 0.0]; case {'K-Alpha'} WAVELENGTHS = [ 1.0 (d.kAlpha1-d.Lambda)/d.Lambda ; d.kAlphaRatio (d.kAlpha2-d.Lambda)/d.Lambda ]; otherwise warning('usedWavelength type not supported (using K-Alpha 1)') WAVELENGTHS = [1.0 0.0]; end % add diffraction lines (anatase - database) a0(1,:) = [56 36.95 0.2 0.5]; % (103) a0(2,:) = [88 37.79 0.2 0.5]; % (004) a0(3,:) = [36 38.57 0.2 0.5]; % (112) % set refined lines parameters Linda(1,:) = [1 1 1 0]; % (103) Linda(2,:) = [1 1 1 1]; % (004) Linda(3,:) = [1 1 1 0]; % (112) results(1).hkl = [1 0 3]; results(2).hkl = [0 0 4]; results(3).hkl = [1 1 2]; % add linear background b0 = [0.0 0.0]; % fit all scans for k=1:length(d.Psi) x = d.Theta2(k,:); y = round(d.data(k,:)*d.time); w = 1./y; [a,b,da,db] = pseudoVoigtFit(x,y,w,a0,b0,[],Linda); yc = sum(pseudoVoigt(a,x),1) + polyval(b,x); for m=1:length(results) results(m).T2(k,1) = a(m,2); results(m).dT2(k,1) = da(m,2); end plot3( x , repmat(d.Psi(k),1,size(d.data,2)) , yc , 'k' ) end % calc lattice planes distaces and their deviations for m=1:length(results) th = results(m).T2*pi/360; results(m).d = d.Lambda./2./sin(th); results(m).dd = cos(th)/d.Lambda.*results(m).d.^2.* ... results(m).dT2*pi/180; end % create sin^2(Psi) plots x = sin(d.Psi*pi/180).^2; for m=1:length(results) figure y = results(m).d; e = results(m).dd; [results(m).p,results(m).dp] = linfit(x,y,e); if ~exist('OCTAVE_VERSION'), %#ok<EXIST> errorbar( x , y , e , 'k*' ), hold on else plot( x , y , 'k*' ), hold on, end plot( x , results(m).p(1)*x+results(m).p(2) , 'k' ) xlim( [-0.03, 0.9] ) xlabel( 'sin^2(Psi)' ), ylabel ( 'd (A)' ) str = sprintf('ANATASE (%d%d%d)', results(m).hkl); title( str ) end % print results for m=1:length(results) str = sprintf(' ANATASE DIFFRACTION LINE (%d%d%d)\n', ... results(m).hkl); str = [ str sprintf('%14s%26s\n','Psi (deg)','2Theta (deg)') ]; str = [ str sprintf('%14.4f%15.4f +/- %6.4f\n', ... [d.Psi results(m).T2 results(m).dT2]' ) ]; str = [ str sprintf(' D(HKL) VS. SIN^2(PSI)\n') ]; str = [ str sprintf('%31s%23s\n','slope','intercept (A)') ]; str = [ str sprintf('%15.4e +/- %11.4e %10.5f +/- %7.5f\n', ... [results(m).p; results(m).dp]) ]; disp(str) end
Fitted peak positions and coefficients of the Sin2(Psi) linear regression are here (script output).
ANATASE DIFFRACTION LINE (103) Psi (deg) 2Theta (deg) 0.0000 37.0162 +/- 0.0026 21.7200 37.0043 +/- 0.0032 31.5500 36.9966 +/- 0.0031 39.8600 36.9825 +/- 0.0030 47.7300 36.9717 +/- 0.0029 55.8300 36.9659 +/- 0.0029 65.0000 36.9553 +/- 0.0033 D(HKL) VS. SIN^2(PSI) slope intercept (A) 4.7374e-03 +/- 2.5945e-04 2.42867 +/- 0.00012 ANATASE DIFFRACTION LINE (004) Psi (deg) 2Theta (deg) 0.0000 37.8637 +/- 0.0006 21.7200 37.8516 +/- 0.0008 31.5500 37.8386 +/- 0.0009 39.8600 37.8261 +/- 0.0009 47.7300 37.8164 +/- 0.0009 55.8300 37.8072 +/- 0.0009 65.0000 37.8032 +/- 0.0011 D(HKL) VS. SIN^2(PSI) slope intercept (A) 4.7994e-03 +/- 6.7711e-05 2.37628 +/- 0.00003 ANATASE DIFFRACTION LINE (112) Psi (deg) 2Theta (deg) 0.0000 38.6202 +/- 0.0072 21.7200 38.6158 +/- 0.0045 31.5500 38.5956 +/- 0.0038 39.8600 38.5897 +/- 0.0032 47.7300 38.5812 +/- 0.0026 55.8300 38.5686 +/- 0.0025 65.0000 38.5572 +/- 0.0027 D(HKL) VS. SIN^2(PSI) slope intercept (A) 4.5411e-03 +/- 3.1286e-04 2.33126 +/- 0.00018
Download
- example3.m (src)
- TiO2_STRESS.xrdml (data)
- peak-fitting-functions.zip
(compressed src)
- linfit.m (src)
Comment: Please note you need additional peak fitting functions and the linfit function to run this example.
See Add-ons section for more details.