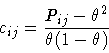8.3 Correlations

Diffuse scattering contains two-body information of the system under investigation and is thus a valuable source how atoms or molecules interact. In contrast Bragg scattering can only reveal average one-body information such as atomic positions, site occupancies and thermal ellipsoids. In this chapter the concept of correlations as a measure for those two-body interactions will be introduced. Although diffuse scattering contains only information about two-body interactions the concepts described here can easily be extended to include multi-site correlations. It should be noted that although these multi-site interactions do not show up in the diffraction pattern directly, they can have a constraining influence on two-body interactions and thus effecting the diffraction pattern. However, DISCUS is currently limited to the calculation of two-body interaction averages.

We will talk about atom types in the following section, however, all correlation related commands are available for molecules as well. To work with molecules use the command 'mode mole' and specify molecule types rather than atom types or names as parameters for the commands. The command 'homo' (see section 8.1) can also be used to determine the homgeniety of correlations within the crystal.

   
8.3.1 Occupational correlations

First occupational correlations will be discussed. One definition of the correlation coefficient c_ij between a pair of sites i and jbased on a statistical definition of correlation [28] is given in equation 8.1.

$$c_{ij} = \frac {P_{ij} - \theta^{2}} { \theta (1 - \theta)}$$ (8.1)

P_ij is the joint probability that both sites i and j are occupied by the same atom type and $\theta$ is its overall occupancy. Negative values of c_ij correspond to situations where the two sites i and jtend to be occupied by different atom types while positive values indicate that sites i and j tend to be occupied by the same atom type. A correlation value of zero describes a random distribution. The maximum negative value of c_ij for a given concentration $\theta$ is $-\theta/(1-\theta)$ (P_ij=0), the maximum positive value is +1 ( $P_{ij}=\theta$). This definition of correlations can easily be converted to the Warren-Cowley short-range order parameter $\alpha_{lmn}^{ij} = 1 - P_{lmn}^{ij} / \theta$ [5]. As an example the correlations $c_{\langle 10 \rangle}$ and $c_{\langle 11 \rangle}$ of the disordered structure shown in figure 8.1 are calculated using the DISCUS macro file listed below:

     1  read
     2  stru chem.1.stru
     3  #
     4  chem
     5  #
     6  set mode,quick,periodic
     7  #
     8  set vec,1,1,1, 1, 0, 0
     9  set vec,2,1,1,-1, 0, 0
    10  set vec,3,1,1, 0, 1, 0
    11  set vec,4,1,1, 0,-1, 0
    12  #
    13  set vec,5,1,1, 1, 1, 0
    14  set vec,6,1,1,-1, 1, 0
    15  set vec,7,1,1, 1,-1, 0
    16  set vec,8,1,1,-1,-1, 0
    17  #
    18  set neig,vec,1,2,3,4
    19  set neig,add
    20  set neig,vec,5,6,7,8
    21  #
    22  corr occ,zr,void
    23  #
    24  exit

The macro starts with the reading of the disordered structure (lines 1-2). After the 'chem' sublevel is entered (line 4) periodic crystal boundaries are selected (line 6). The parameter 'quick' selects a faster neigbouring finding algorithm which only works for crystals arranged in the DISCUS storage order (see section 2.2). Note that $c_{\langle 10 \rangle}$ stands for the nearest neighbour correlations in all four symmetrically equivalent <10> directions of the two dimensional cubic test crystal, i.e. c₁₀, $c_{\overline{1}0}$, c₀₁ and $c_{0 \overline{1}}$. All eight neigbouring directions for $c_{\langle 10 \rangle}$ and $c_{\langle 11 \rangle}$ are defined as vectors 1 to 8 in lines 8 to 16 of the macro file. Next vectors 1 to 4 are grouped as neighbouring definition for $c_{\langle 10 \rangle}$ (line 18) and vectors 5 to 8 for $c_{\langle 11 \rangle}$ (line 20). The command 'set neig,add' (line 19) stores the current neighbouring definition and allows the definition of a new one. Finally the correlations for the defined neighbouring directions are calculated (line 22). The screen output for the disordered structure shown in figure 8.1 looks like this:

    Calculating correlations
        Atom types : A = ZR   and B = VOID

        Neig.     AA         AB         BB         # pairs    correlation
        -----------------------------------------------------------------
           1    50.49 %    48.99 %      .51 %       40000       -.3061
           2    71.04 %     7.89 %    21.07 %       40000        .7897

The program lists the probabilities for AA, AB and BB pairs and the corresponding correlations c_ij. Here the value for $c_{\langle 10 \rangle}$ is negative, i.e. vacancy neighbours in <10> directions tend to be avoided. Neighbouring vacancies in <11> direction on the other hand are much more likely compared to a random vacancy distribution indicated by the large positive value of $c_{\langle 11 \rangle}$. This leads to the large areas with a doubled unit cell and a Zr concentration of 0.5 as seen in section 8.1.

   
8.3.2 Displacement correlations

The correlation coefficient c_ij for displacement correlations between two sites i and j is defined as:

$$c_{ij} = \frac { \langle x_{i} x_{j} \rangle } { \sqrt { \langle x_{i}^{2} \rangle \langle x_{j}^{2} \rangle } }$$ (8.2)

Here x_i is the displacement of the atom on site i from the average position in a given direction and $\langle \cdot \rangle$ stands for the average over the crystal. Again a negative value describes a situation where the pairing of corresponding displacements are less likely than in a crystal with random displacements whereas a positive value indicates a larger than random probability. The definition of neighbours is identical to the example in the previous section. Additionally the command 'set neig,dir' is used to determine the displacement direction to be used. Note that the displacement direction for the two sites i and j is not necessarily the same, e.g. one could be interested in the correlation between the x-displacement on one site and the y-displacement on the neighbouring site.

   
8.3.3 Correlation fields

In the previous sections a correlation c_ij for a given pair of neighbouring atoms was computed. An interesting information, however, is how these correlations extend within the crystal. The program DISCUS allows the calculation of correlation fields for occupational and displacement correlations (command: 'field').

  

Figure 8.3: Example for a correlation field

Again taking the disordered structure displayed in figure 8.1 as an example, the correlation fields in <10> and <11> direction are shown in figure 8.3. This figure shows the correlation between a site i and sites separated by integer multiples of the vectors used in the neighbor definitions. The neighbouring definitions are the same as in the example for a single correlation coefficient in section 8.3.1. The first neighbour correlation is negative for $c_{\langle 10 \rangle}$ and positive for $c_{\langle 11 \rangle}$ as in section 8.3.1. The correlation $c_{\langle 11 \rangle}$ is decaying as a function of the distance within the crystal, giving a measure of the extension of the area with preferred <11> vacancy neighbours. Eventually the value gets negative for distances above about 26 times the $c_{\langle 11 \rangle}$ vector which can be understood taking the size of the two phase regions (figure 8.1) into account. The absolute value of correlation $c_{\langle 10 \rangle}$ decays as well but oscillates between negative an positive values. This can be understood by thinking of a perfect ABAB sequence. All odd neighbours (i.e. 1,3,5, ...) are AB or BA resulting in a negative correlation whereas even neighbours (i.e. 2,4,6, ...) are AA or BB giving a positive correlation.