F

Difrakce rtg. záření na krystalických látkách, dynamická teorie

 

Václav Holý – Dušan Korytár

 

 

1. Srovnání kiematické a dynamické teorie difrakce rtg. záření.

Terminologie používaná v kinematické teorii difrakce rtg. záření je shrnuta v kapitole C autorů I. Červeň, V. Valvoda. Tato kapitola bude zde citována jako ČV.  V několika případech se terminologie používaná v oblasti dynamické teorie podstatně liší, na to upozorníme na patřičném místě textu.

Základem kinematické teorie rtg. difrakce jsou tyto předpoklady:

1.      Procházející vlna (1) není ovlivněna existencí difraktované vlny (2),  a je tedy totožná s primární vlnou (viz ČV).

2.      Difraktovaná vlna dále v krystalu nedifraktuje a vychází z něj ven. Zanedbává se tedy vícenásobná difrakce (3) vlnění v krystalu.

Z předpokladu 1. je zřejmé, že kinematická teorie difrakce nebere ohled na zákon zachování energie rtg. záření při difrakci. Uvedené předpoklady odpovídají Bornově aproximaci (4) v obecné teorii rozptylu.

           

Kinematickou teorii lze použít pro popis směrů šíření difraktovaného vlnění (geometrie difrakce (5)) tento výpočet však nebude brát v úvahu lom rtg. záření (6) na povrchu krystalu. Intenzitu difrakce je možno počítat kinematicky pouze tedy, je-li možno zanedbat vícenásobnou difrakci vlnění v krystalu. Toto zanedbání je možné provést

1.      v případě ideálních krystalů, jsou-li jejich rozměry menší než extinkční délka rtg. záření

2.      v případě porušených krystalů, je-li střední velikost koheretní oblasti krystalové struktury (viz ČV) menší než extinkční delka rtg. záření.

V ostatních případech, a pro výpočet prošlé vlny ve všech případech, je nutno použít dynamickou teorii difrakce rtg. záření (7). Difrakční jevy, které nelze vysvětlit kinematickou teorii difrakce, a k jejichž popisu je nutná dynamická teorie, se nazývají dynamické difrakční jevy (8).

 

2. Rtg. vlnové pole (9) v krystalu

            Rtg. vlnové pole v krystalu se popisuje pomocí vektoru elektrické indukce (10)  D(r, t). Z Maxwellových rovnic plyne pro vektor D vlnová rovnice (11) ve tvaru

 

Veličina   je v případě dokonalého krystalu periodickou funkcí souřadnic. Platí pro ni vztah

 

kde   je relativní permitivita krytalu. Předpokládáme-li   » 1, a omezíme-li se na případ, kdy se energie fotonů rtg. záření podstatně liší od ionizační energie elektronů v atomovém obalu, je  úměrné elektronové hustotě (12) elektronů účastnících se rozptylu rtg. záření na atomech. Za uvedeného předpokladu je totožné s elektrickou susceptibilitou krystalu (13).

Poznámka: Termín používaný v anglosaské i ruské literatuře, který lze do češiny přeložit jako polarizibilita, je odlišný od polarizovatelnosti elektrického dipólu, tak jak je zavedena v elektrodynamice dielektrik a není proto vhodné takto veličinu  χ označovat.

 

            Rovnici (f1) lze použitím Greenovy funkce pro volnou částici (14) převést do integrálního tvaru a tento řešit postupými iteracemi. První iterace pak odpovídá difrakci v rámci kinematické teorie. Vlnové pole v dynamicky difraktujícím krystalu však nelze získat iteračním řešením rovnice (f1). Protože je v ideálním krystalu periodickou funkcí souřadnic, lze za předpokladu monochromatičnosti vlnění hledat řešení rovnice (f1) ve tvaru Blochovy vlny (15)

 

kde  g  jsou vektory reciproké mřížky,  je vlnový vektor z 1. Brillouinovy zóny (16) reciprokého prostoru. Z rovnice (f1) pak plyne, že koeficienty  jsou kořeny homogenního systému algebraických rovnic

kde    je p-tý koeficient rozvoje funkce   do Fourierovy řady

a dále platí

 

3. Jednovlnová a dvouvlnová aproximace

            V případě, že odchylka směru rovinné rtg. vlny dopadající na krystal (primární vlna – viz ČV) od směru, který vyhovuje difrakční podmínce (viz ČV) je pro danou vlnovou délku dostatečné velká, lze přibližně předpokládat, že se krystalem šíří pouze jediná rovinná vlna (jednovlnová aproximace (17)). Z rovnice (f3) pak plyne podmínka existence takové vlny ve tvaru . Geometrickým místem koncových bodů vlnových vektorů  , které vyhovují této podmínce, je kulová plocha o poloměru  k = nK,  t.j. Ewaldova kulová plocha (viz ČV), kde    je index lomu (18) rtg.  záření v krystalu. Vždy platí  n < 1 a hodnota 1 – n je řádově . Veličina  je úměrná elektronové hustotě v krystalu středované přes základní buňku.

           

Odpovídá-li směr primární vlny přibližně difrakční podmínce, lze v řadě  (f2) zanedbat všechny členy kromě členů s g = 0 (prošlá vlna) a g = h (difraktovaná vlna), kde h je difrakční vektor (v kinematické teorii rtg difrakce je obvyklé značit difrakční vektor jako  S ).  Tento případ se nazývá dvouvlnová aproximace (19). V krystalu pak existují vlny

 

 

právě tehdy, vyhovuje-li vektor disperzní podmínce (20)

 

 

kde . Geometrické místo koncových bodů vektorů   vyhovujících podmínce (f5), se nazývá dvouvlnová disperzní plocha (21). Veličina C je polarizační faktor (22) vlnění a je roven 1 pro s-polarizaci (s-polarizaci) (23) vlnění nebo    pro p-polarizaci (-polarizaci) (24) vlnění. Poznámka: Střední hodnota čtverců těchto polarizačích faktorů odpovídá polarizačnímu faktoru pro nepolarizované záření, který se užívá v kinematické teorii difrakce.

           

Pro body pro něž je , lze vztah (f5) zjednodušit a dostaneme disperzní podmínku

 

 

Průsečnice jí odpovídající disperzní plochy s difrakční rovinou (25), tedy s rovinou určenou vektory  a  , má v okolí bodu reciprokého prostoru, v němž je   (Lorentzův bod (26)), tvar hyperboly. Její dvě větve (27) se asymptoticky blíží ke kružnicím (v okolí Lorentzova bodu nahrazenými přímkami), které jsou průsečnicemi Ewaldových kulových ploch o poloměru k = nK s difrakční rovinou. Středy těchto kulových ploch leží v bodech reciproké mřížky spojených difrakčním vektorem h. Sestrojíme-li v týchž středech Ewaldovy kulové plochy s poloměry K (t.j. Ewaldovy kulové plochy pro vakuum), jejich průsečnice s difrakční rovinou budou opět kružnice a jejich průsečík se nazývá Laueho bod (28). Odpovídá-li (přibližně) směr primárního vlnění difrakčním podmínkám více difrakcí (např. n), je nutno v řade (f2) ponechat n+1 členů, které odpovídají prošlé vlně a n difraktovaným vlnám. Tento případ se nazývá (n+1)-vlnová aproximace (29) a její experimentálním důsledkem je Renningerův jev (30).

 

 

            4. Difrakce na ohraničeném krystalu

Při výpočtu vlnového pole uvnitř krystalu je nutno kromě rovnice (f3) a disperzní podmínky (f5) resp. (f6) uvážit okrajové podmínky (31) pro vlnění na vstupním (32) a výstupním (33) povrchu krystalu. Protože je plyne z Maxwellových rovnic, že se ve většině případů zachovává vektor D na rozhraní vzduch-krystal, a tedy že se na tomto rozhraní zachovává amplituda vlnění a tečná zložka vlnového vektoru.

V dynamické teorii difrakce je obvyklé ztotožňovat koncové body vlnových vektorů  (vlnový vektor primární vlny),  (vlnový vektor prošlé vlny vně krystalu) v témže bodě reciproké mřížky (bod O (34)) a koncové body vlnových vektorů kh , Kh (vlnový vektor difraktované vlny vně krystalu) v témže bodě H (35) reciproké mřížky. Potom budou počáteční body všech těchto vektorů ležet na společné vnitřní normále (36) k vstupnímu povrchu krystalu. Počáteční body vektorů  ,  resp. Kh budou kromě toho ležet na Ewaldově kulové ploše ve vakuu se středem v bodě  O resp. H, počáteční body vektorů , kh budou ležet na disperzní ploše (f5). Vnitřní normála k povrchu krystalu protíná tuto disperzní plochu v uzlových bodech (37). Poznámka: Tyto uzlové body nesouvisí s uzlovými body reciproké mřížky, proto je lépe používat termín body reciproké mřížky.V dvouvlnové aproximaci je v okolí Lorentzova bodu počet uzlových bodů roven buď 2 (normála protíná obě větvy hyperboly nebo jedinou větev dvakrát) nebo 0 (normála prochází mezi větvemi hyperboly – tento případ lze formálně popsat komplexními vlnovými vektory , kh ). V prvním případě se krystalem pro každou polarizaci šíří čtveřice vln:

 

 

 

 

V druhém případě se vlnění v krystalu rychle utlumí a dochází k zrkadlovému odrazu vlnění (38) (totálnímu odrazu) na povrchu krystalu. Poznámka: Tento jev je způsoben difrakcí vlnění a nesouvisí s odrazem vlnění na rozhraní dvou opticky různých prostředích.

            Okrajové podmínky na výstupním povrchu krystalu jsou obdobné. Podle úhlů  mezi difrakčním vektorem a jednotkovými vektory   vnitřních normál ke vstupnímu, resp. výstupnímu povrchu krystalu rozlišujeme tyto případy:

 

1

uspořádání  „Laue – Laue“      

(39)

2

uspořádání  „Bragg – Bragg“

(40)

3

uspořádání  „Laue – Bragg“

(41)

4

uspořádání  „Bragg – Laue“

(42)

 

            Jsou-li vstupní a výstupní povrch krystalu rovinné a planparalelní, je     a mohou se realizovat uspořádání 1. a 2. Uspořádání „Laue – Laue“ se pak nazývá Laueho případ (uspořádání na průchod) (43), uspořádání  „Bragg – Bragg“ se nazývá Braggův případ (uspořádání na odraz) (44), na planparalelním krystalu.  Poznámka: Uspořádání na odraz nesouvisí s „odrazem“ rtg záření, proto je vhodnější užívat termín Braggův případ. Je-li   , v difrakci na průchod nebo  ,   v Braggově případě, hovoříme o symetrické difrakci (45) v Laueho nebo Braggově případě. V symetrické difrakci je úhel mezi primárním paprskem a vstupním povrchem stejný, jako úhel mezi difraktovaným paprskem a výstupním povrchem krystalu.

 

 

5. Některé dynamické difrakční efekty

Měřená veličina při rtg difrakci (tok fotonů rtg záření okénkem detektoru nebo sčernání fotografické emulze) je v případě homogenního vlnového pole dána Poyntingovým vektorem vlnění, který je úměrný veličině

 

 

kterou nazýváme intenzita rtg záření. Poznámka: Takto definovaná intenzita rtg záření je funkcí souřadnic. V dynamické teorii difrakce, na rozdíl od kinematické teorie, není intenzita záření spojena s určitým směrem šíření.

             

            Rtg reflexní křivka  (46), resp. transmisní křivka  (47) je závislost poměru toku (t.j. součinu intenzity a průřezu svazku) difraktovaného resp. prošlého vlnění na odchylce h směru primárního vlnění od směru, který odpovídá difrakční podmínce. Pojem reflexní, resp. transmisní křivky se zavádí pouze pro difrakci na planparalelním krystalu a pro rovinnou monochromatickou primární vlnu. Reflexní křivka se někdy charakterizuje svoji šířkou v poloviční výšce (48). Poznámka: Někdy užívaný termín pološířka je matoucí, lépe neužívat. Tato veličina závisí na faktoru asymetrie difrakce (49)

 

a na hodnotě  

            Měřením závislosti intenzity záření difraktovaného dvojkrystalovým (nebo vícekrystalovým) difraktometrem (50) na vzájemné uhlové poloze krystalů získáme difrakční křivku (51) jako konvoluci reflexních křivek 1. a 2. krystalu.

            Integrální intenzita difrakce (52) se definuje jako

 

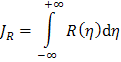
a číselně odpovídá ploše pod rtg reflexní křivkou. Obdobně se definuje integrální intenzita transmise (integrální intenzita prošlého vlnění) (53) jako

 

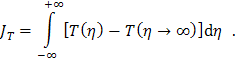
Poznámka: Význam těchto pojmů se v dynamické teorii podstatně liší od pojmů označených stejným názvem v kinematické teorii. Zatím co v kinematické teorii jde o integrál směrové závislosti intenzity přes prostorový úhel, v němž leží vlnový vektor difraktované vlny, v dynamické teorii jde o integrál intenzity přes úhly dopadu primárního vlnění, přičemž se předpokládá, že dopadající i difraktované vlnění je rovinné. Z tohoto důvodu je pojem intenzita v dynamické teorii analogický pojmu integrální intenzita v kinematické teorii.

 

            Interferencí vlnových polí s amplitudami  vzniká postupní vlnění s modulovanou amplitudou. Maxima amplitudy leží v rovinách rovnoběžných s povrchem krystalu. Vzdálenost těchto rovin sa nazývá extinkční hloubka (extinkční délka) (54) rtg záření v krystalu.  Poznámka: Tato veličina nesouvisí s koeficientem extinkce uvedeným v kinematické teorii, a jen nepřímo souvisí s primární extinkcí rtg záření.

 

            Maxima amplitudy prošlého vlnění leží uprostřed mezi rovinami maxim amplitudy vlnění difraktovaného. S rostoucí hloubkou pod povrchem krystalu tedy dochází k periodickému „přelévání“ energie z difraktovaného do prošlého vlnění a zpět, které připomíná pohyb zpřažených kyvadel. Proto se tento jev nazývá pendellösung (55). Díky němu existují ekvivalentně rozložená maxima a minima intenzity a integrální intenzity difrakce v závislosti na tlouštce krystalu, které způsobují „proužkování“ difrakčních stop při difrakci na klinovitém krystalu – proužky jevu pendellösung (56).  Poznámka: Slovo pendellösung se neskloňuje.

           

            Je-li tlouštka krystalu T  větší než   , kde    je lineární absorpční koeficient rtg  záření (57), pozorujeme v transmisní křivce maximum vyšší než   V tomto maximu má krystal anomální propustnost (58). Existence anomální propustnosti se nazývá Borrmannův jev (59).

 

            Interferencí vlnových polí s amplitudami Dh1  a  D01  (resp. Dh2  a  D02) vzniká rtg stojatá vlna (60) s kmitnami rozloženými v rovinách kolmých na difrakční vektor. Vzdálenost sousedních kmiten je dána mezirovinnou vzdáleností rovin atomů, na nichž dochází k difrakci. Poloha kmiten stojaté vlny v krystalové struktuře závisí na odchylce h směru primární vlny od směru daného difrakční podmínkou. To se využívá v metodách užívajících stojatou vlnu (61) pro sledování poruch krystalové struktury.

 

 

            6. Dynamická rtg difrakce na krystalech s poruchami

            Intenzita záření difraktovaného (resp. prošlého) porušenou oblastí krystalu je jiná než v případě dokonalého krystalu, dochází k difrakčnímu kontrastu (62). Příčiny difrakčního kontrastu jsou:

            1. lokální změna efektivní rozorientace krystalové struktury (63) v níž je zahrnuta změna orientace i vzdáleností mřížkových rovin – tzv. orientační kontrast (64).

            2. křivost mřížkových rovin vede ke změně integrální intenzity difrakce, což vede ke vzniku extinkčního kontrastu (65).

 

            Teoretický popis rtg difrakce na porušených krystalech je předmětem zobecněné dynamické teorie rtg difrakce (66). V tzv. formalizmu rovinných vln (67) se vychází z předpokladu, že porušeným krystalem se šíří rtg vlnění ve tvaru modifikované Blochovy funkce (68)

 

kde   jsou pomalé funkce souřadnic. Za předpokladu malých deformací lze pak   najít jako řešení jistého systému lineárních parciálních rovnic 1. řádu – Takagiho rovnice (69).

 

            V tzv. eikonálovém formalizmu (70) se vlnění v porušeném krystalu popisuje pomocí paprskových trajektorií (71), jejichž tvar v deformovaném krystalu závisí na jeho lokálních disperzních plochách (72). Tento přístup souvisí s popisem rtg vlnového pole v krystalu pomocí kulových vln.           

 

 

Komentář

Předkládaný text postihuje pouze terminologii teorie dynamické rtg difrakce a to pouze jejich základů. Bohatá terminologie experimentálních metod založených na dynamické difrakci bude předmětem jiné kapitoly.

Autoři jsou si vědomi toho, že existuje značná nekonzistence terminologií běžných v kinematické a v dynamické difrakci. Nekladli jsme si za cíl vytvořit jedinou terminologii, ale postihnout názvosloví tak, jak se skutečně užívá.