A program for automatic checking of crystal structure solution results based on comparison with DFT calculation results

F. Fňukal

University of Chemistry and Technology, Prague, Technická 5, 166 28 Praha 6 – Dejvice

fnukalf@vscht.cz

Introduction
Crystal structure verification based on the comparison with DFT calculation results was already introduced circa 20 years ago [1, 2]. However, only the advancement in computing technology as well as the development in the area of DFT functionals made it possible to perform such calculations on complex organic molecular crystals. Our aim is to develop a program capable of mediating DFT calculations and analysing the results. There already exist commercial pieces of software offering such capabilities, they are however typically fairly expensive. Our aim is therefore also to present a freely available variant of such software.

Crystal structure verification using dispersion-corrected DFT
A DFT calculation uses an experimental structure as an input. During the calculation, the atomic positions and optionally also the cell parameters are optimized in a way that the energy minimum is achieved. The output of a DFT calculation is another structure with a geometry more or less different from the geometry of the experimental structure. The input and output structures can then be compared based on certain selected criteria. These criteria should indicate serious discrepancies in the two structure geometries.

Our implementation – the program checkCIF-DFT
To facilitate performing DFT calculations on crystal structures we developed a program to which we gave the name checkCIF-DFT. An inspiration to us was the web application checkCIF/PLATON [3], which offers consistency and validity checking for experimental crystal structures based on crystallographic diffraction criteria. Our program intrinsically utilizes 3 different DFT programs: Quantum ESPRESSO [4], CASTEP [5] and Orca [6]. Besides that, the molecular mechanics program GULP [7] is also utilized. Our program provides a graphical interface and serves as a mediator between the user and computational programs. Our program can read and visualize data from a CIF file, prepare input files for computational programs, monitor the progress of a calculation and finally, after a calculation has finished, it can analyse the calculation results and point out serious issues.

Figure 1. Main window of the program checkCIF-DFT.

Input and output structures comparison
To compare the experimental crystal structure and the DFT output crystal structure, it is absolutely essential to choose comparison descriptors that are sufficiently indicative and can therefore reflect serious discrepancies in the compared structures. In our work, we originally used solely the descriptor RMSCD developed by other authors [2]. However, as the authors of RMSCD stated themselves, this descriptor doesn’t reflect serious issues well enough. For that reason, we decided to include other descriptors. Among the newly implemented descriptors are relative difference in cell volumes, maximal difference in bond lengths, maximal difference in bond angles and others. In our testing so far, we discovered that the tested problematic structures reliably exhibit a serious disagreement in at least one of the used descriptors.

Practical uses of DFT calculation results
DFT calculations can be used for routine verification of experimental crystal structure solutions. Some experimental results may be affected by serious errors due to bad quality of the crystalline sample or other factors. For that reason, a DFT calculation can be useful to assess the trustworthiness of the experimentally obtained data.
Crystal structure prediction represents another field of use for DFT calculations. In such computational experiment a large set of possible crystal structure geometries is generated using lower-level methods (e.g. molecular mechanics). These structures are then refined using the DFT method. The refined set of structures can then be sorted based on the lattice energy, which should reflect the stability of each structure in the set.
Apart from the two examples mentioned above, DFT calculations also find great use in powder diffraction crystal structure solutions. While solving powder diffraction data, a DFT calculation can be used as an intermediate step to achieve a better level of refinement.

DFT method testing
In our work, we’ve conducted a series of testing calculations to assess how well the DFT method would fare in indicating seriously erroneous crystal structure solutions. In our testing, we chose a set of 5 structures that are known to be fraudulent [8] and a set of 5 structures solved by neutron diffraction experiments, which we deemed to be the most precise and reliable method of determining the crystal structure. For this test we used the CASTEP computational module utilizing the rSCAN functional and MBD dispersion correction. When analysing the results, we concluded that the DFT method together with our improved descriptor system was able to detect that the fraudulent structures were erroneous (Fig. 2).

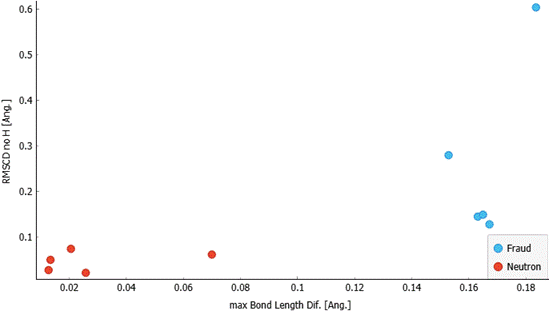
Figure 2. Scatterplot of RMSCD excluding hydrogen atoms against maximal bond length difference for a set of structures solved using neutron diffraction data (red) and a set of structures that are known to be fraudulent (blue).

We also used the DFT method in a crystal structure prediction computational experiment. DFT calculations were performed on a set of 100 trial structures with the code XXXI from the 7^th CSP Blind Test [9]. In this test we used the Quantum ESPRESSO computational module utilizing the PBE functional and D3 dispersion correction. Using our method, we were able to capture the 3 experimentally observed polymorphs among the first 8 structures with lowest calculated lattice energies (Tab. 1). The DFT method is however known to not yield perfect results in this type of crystal structure prediction experiment, mainly due to difficulties in describing thermal effects.

Table 1. Best 10 trial structures of the compound XXXI from the 7th CSP Blind Test as calculated by the DFT method.

Rank	Structure code	Relative energy [kJ/mol]	Experimental rank
1.	XXXI_structure_59	0.0000	-
2.	XXXI_structure_98	0.7963	1.
3.	XXXI_structure_1	2.0061	2.
4.	XXXI_structure_17	2.5395	-
5.	XXXI_structure_57	2.9341	-
6.	XXXI_structure_34	3.0854	-
7.	XXXI_structure_11	3.1684	-
8.	XXXI_structure_25	3.2349	3.
9.	XXXI_structure_70	3.4779	-
10.	XXXI_structure_20	4.1705	-

Conclusions
In our work, we discovered that we were able to detect fraudulent crystal structures using DFT calculations together with an improved system of structure comparison descriptors. The most useful comparison descriptors have shown to be the maximal bond length difference and maximal bond angle difference.
We developed and tested a freely available program that is capable of mediating DFT calculations and analysing the results. This program may help crystallographers in assessing the trustworthiness of crystal structure solutions.

1. J. Streek, M. A. Neumann, Acta .Cryst., B66, (2010), 544.

2. J. Streek, M. A. Neumann, Acta .Cryst., B70, (2014), 1020.

3. (IUCr) IUCr Journals - checkCIF FAQ. https://journals.iucr.org/services/cif/checking/checkfaq.html#what (accessed May 10, 2024).

4. Paolo Giannozzi et al, J. Phys.: Condens. Matter, 21, (2009), 395502

5. Materials Studio 2023 - CASTEP. https://www.tcm.phy.cam.ac.uk/castep/documentation/WebHelp/CASTEP.html (accessed May 10, 2024).

6. F. Neese, Wiley Interdisciplinary Reviews: Computational Molecular Science, 2, (2012), 73

7. J. Gale, J. Chem. Soc., Faraday Trans., 93, (1997), 629

8. The Lancet, 375, (2010), 94

9. The 7th CSP Blind Test | CCDC. https://www.ccdc.cam.ac.uk/community/ccdc-for-the-community/partnerships-and-initiatives/csp-blind-test/7th-csp-blind-test/ (accessed May 10, 2024).