AZINT-practical: Shaping 2D synchrotron data for Rietveld refinement
Z. Matěj
MAX IV Laboratory, Lund University, Sweden
zdenek.matej@maxiv.lu.se
Rietveld refinement [1] is a widely recognized method of analysis of X-ray and neutron powder diffraction data for the characterization of various aspects of crystalline materials. In case of X-rays, the powder diffraction data can be acquired using a range of instruments including dedicated industrial and laboratory diffractometers or highly optimized powder diffractometers at synchrotron beamlines. Given the valuable insights that powder X-ray diffraction can offer, this technique is frequently employed in multimodal experiments or as a supplementary method in the beamlines at accelerator-based photon sources.
|
|
|
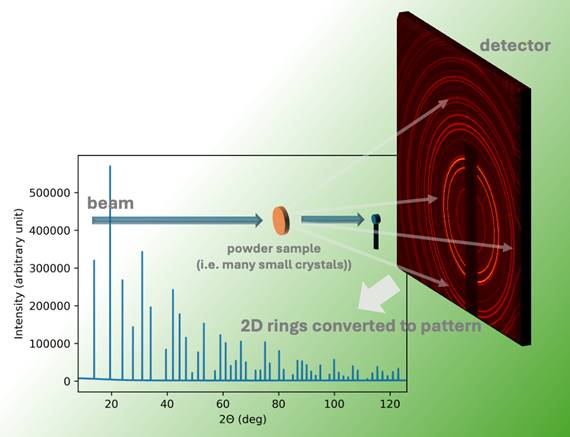
Figure 1. The transmission X-ray diffraction geometry with a flat area detector in the forward direction. |
The most prevalent scattering geometry at the light sources today is the transmission (Debye-Scherrer like) geometry with a flat area detector positioned in the forward direction (Fig. 1). This experimental geometry is straightforward to implement, it takes advantage of intensive X-ray diffractions at lower scattering angles, and by utilizing large, fast area detectors, it delivers sub-millisecond time resolution with robust signal strength and a decent angular resolution.
Furthermore, area detector data can yield additional information on the preferred orientation of crystallites (texture) in the sample. When texture information is not the primary focus, the area detector data are typically reduced to 1D diffraction patterns, which offer a standard representation of the diffraction experiment and serve as input for the Rietveld method.
There are numerous dedicated software options for azimuthal integration (AZINT) of the area detector data, including fit2d [2], PyFAI [3], diffpy.srxplanar [4], Nika [5], and AZINT-module [6,7]. While some of these computer programs were initially designed for small angle scattering data, they often extend their applicability to the powder diffraction modality.
Complementary to AZINT software there are multiple software options for the Rietveld refinement. A non-exhaustive list includes FullProf [8], GSAS II [9] and EXPGUI [10], Maud [11], TOPAS [12], Jana2020 [13] or MStruct [14]. Only two of these software [9-11] provide an “all in one solution” that also covers the AZINT reduction step and detector calibration.
Beamlines at light sources often include the AZINT reduction step as part of their automated data processing workflow [6,15], so users may choose to bypass the internal AZINT step in the latter software as well. AZINT software come with numerous settings and can optionally apply several intensity corrections on data, including solid angle correction, polarization correction, air-absorption correction, sample absorption or sample scattering corrections, parallax effect correction, and detector flat-field correction. Other notable options include a “normalization model” [3], “error propagation model” [3] or possible correlation between powder pattern points [4].
Simultaneously, all Rietveld software [8-14] have many options and can account for some of the intensity corrections mentioned above.
This contribution provides an overview of software options for AZINT and the suitable settings for some of the software implementing the Rietveld method.