Modulated structures and twins – a nightmare for crystallographers?

V. Petříček, M.Dušek

Institute of Physics, ASCR, Na Slovance 10, 182 21 Praha, Czech Republic

petricek@fzu.cz

Most standard structures can be solved using "modern programs for solution and refinement of crystal structures" in minutes without understanding what the programs do. Therefore, one may get the impression that structural crystallography is a closed field and that the crystallographers involved in the methods have long since done their job. The crystallographer's task is to measure and identify structures with automatic tools, check the chemistry, prepare figures, describe weak interactions and explain or avoid PLATON alerts.

From time to time, however, problems do occur, and standard programs fail. Apart from poor data and very large structures, the most common cause of such failures is that the structure is modulated or the crystal is affected by twinning. These can create nightmares for busy "structural crystallographers", who are expected to solve several structures daily and not waste time with one structure many days. How, then, explain to the chemists who prepared the crystal that their crystal is not standard?

While crystals affected by twinning require solving a geometric puzzle about how the crystal domains coexist in bulk, modulations in a crystal imply a fundamental change in the understanding of crystal symmetry. The diffraction pattern of modulated structures differs significantly from that of unmodulated structures. For standard structures, all diffraction spots can be indexed using three reciprocal lattice vectors. Modulation in the crystal creates additional satellite spots. So-called modulation vectors must be introduced to index them. Then each diffraction spot is described by (3+d) diffraction indices. This implies that the translational symmetry of the crystal is broken, however, regularly.

Satellite diffraction spots are usually much less intense, and their possible neglection leads to an average structure, which in many cases sufficiently proves the chemical structure of the substance under study. On the other hand, there are also cases when modulations fundamentally affect the physical properties. Then, the information about the actual structure and its change with temperature, pressure, or detailed composition is essential, and the complete solution of modulated structure cannot be avoided.

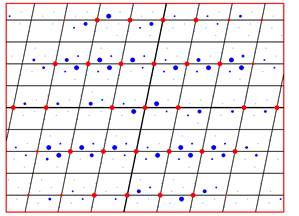
Figure 1. Simulated diffraction pattern of Na₂CO₃ [1]. The main reflections are red, and the satellites are blue.

Measurement, solving and refining modulated structures are analogous to procedures known for ordinary structures. Most modern diffractometers allow multiple indices when integrating diffraction spot intensities. Since the beginning of the 1980s, the possibility of refining modulated structures based on the use of the superspace approach [2] has gradually been included in some programs (REMOS [3], MSR [4], JANA [5]). The program Superflip [6], developed much later, allows for the direct solution of modulated structures without the intermediate step of solving the average structure. All steps of structural analysis are included in Jana2006 [7] or Jana2020 [8] program systems, which try to be user-friendly and reach the situation described at the beginning of this contribution as "the crystallographers involved in the methods have long since done their job". Still, a much deeper knowledge of the fundamentals of modern structural crystallography is required to understand the meaningfulness of results and their interpretation.

In a twinned crystal, each independently diffracting part provides the same diffraction pattern, the position of which is determined by the respective twinning operations. In general, this means that 3n reciprocal vectors must be used to describe the diffraction image of a twin consisting of n independent domains. However, these vectors need not be integer independent, which allows us to distinguish two extreme cases, the fully overlapped and the fully separated twins. The condition for full overlaps means that all twinning matrices reproduce the reciprocal lattice; therefore, their elements are integers, and there are only three integer-independent vectors.    

The observed intensity of the diffraction spots is then the sum of the intensities of the individual domains (1).

                        (1)

where  is the structure factor,  is the volume fraction of the i^th twin domain and  is a square of the resulting structure factor related to the measured intensities.

The above-mentioned condition for complete overlap of diffraction spots of individual domains induces the relation between the lattice and structure point groups. The latter must be a subgroup of the former. The cases with full overlaps are classified as sygnonic and metric merohedry. Determining the point and space group by directly analysing the measured intensities is difficult [9]. Indeed, in the case where the domains are uniformly occupied, the apparent point group is identical to the lattice point group. For non-uniformly occupied domains, the apparent point group is lower than the lattice point group but not necessarily equal to the point group of the crystal structure. On the other hand, in these cases, there is no problem in determining the unit cell.

However, in cases where the number of integer-independent vectors is lower than for completely separated domains but higher than for completely overlapped domains, there is also a problem in determining the proper unit cell of the crystal under study. The twinning matrices are composed of rational numbers, and such twinning is called reticular merohedry. Two cases are presented in fig 2 and 3. No problem can be detected in the first, while in the second, it is evident that the smallest possible cell in the reciprocal space is not the correct choice.

Most conclusions resulting from the analysis of the measured data for twins are more like warnings of potential issues, and it is up to the user to decide how to use such information. The recent version of Jana2020 [8] includes procedures to identify problems that may arise when studying modulated and twin-affected crystals. During the talk, these tools will be presented as examples.

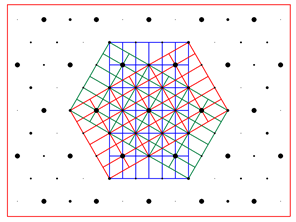
Figure 2. Orthorhombic unit cells in three twin domains of CsLiSO₄.

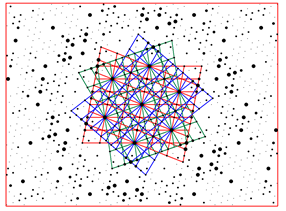
Figure 3. Diffraction pattern of the six-fold twinned structure of β-Ca₁₁B₂Si₄O₂₂ (lattice symmetry 6/mmm, point group 2/m) published in [10]. The first triplet (blue, green and red) shows the unit cells of three twin domains related by the three-fold axis. The second triplet arises from the first one by applying one of the remaining operations of the original hexagonal lattice point group.

1. M. Dušek, G. Chapuis, M. Mayer, V. Petříček, Acta Cryst., B37, (2003), 337.

2. P. M. de Wollf, T. Janssen T., A.Janner, Acta Cryst., A37, (1981), 625.

3. A. Yamamotyo, Acta Cryst., A38, (1982), 87.

4. W. Paciorek, D. Kucharczyk, Acta Cryst., A41, (1985), 462.

5. V. Petříček, P. Coppens, P. Becker, Acta Cryst., A41, (1985), 478.

6. V. Petříček, M. Dušek, L. Palatinus, Z. Kristallogr., 229, (2014),  345.

7. L. Palatinus, G. Chapuis, J.Appl.Cryst., 41 (2007) 786.

8. V. Petříček, L. Palatinus, J. Plášil, M. Dušek, Z. Kristallogr., (2023). https://doi.org/10.1515/zkri-2023-0005

9. V. Petříček, J. Plášil, M. Dušek, Z. Kristallogr., 231, (2016), 583.

10. S.N. Volkov, V.A. Yukhno, R.S. Bubnova, V.V.Shilovskikh, Z. Kristallogr. 233, (2018), 379.