The use of QM calculation for structure refinement - comparison of IAM and HAR refinement results
M. Hušák, S. Chalupná
University of Chemistry and Technology, Prague, Technická 5, 166 28 Praha 6 – Dejvice
husakm@vscht.cz
Introduction
The most often used method for crystal structure refinement is based on Independent Atom Model (IAM). IAM gives identical atomic scattering factors for the same element under any situation ignoring the influence of the surrounding atoms. In reality the atomic scattering factors deepened on the actual electron shell configuration of the atom in the given position and given valence state. The issues with IAM can be handled by three methods: Multipole Model, Transferable Aspherical Atom Model (TAAM) [1] and Hirshfeld Atom Refinement (HAR)[2]. Multipole Model requires high-quality data and additional refinement parameters. TAAM model requires a precomputed database of atomic scattering factors for the given element with different surroundings. For TAAM the calculation can be done correctly only, when the parameters of the element under required configuration were already placed in the database. The recently introduced HAR refinement as implemented in Olex2 software [2] works with any sort of data and does not depend on atom scattering factor database. During HAR refinement the atomic scattering factors are calculated by external quantum mechanic (QM) software like e.g. Orca or Gaussian. The wave function generated by the QM code is than re-calculated in format suitable for the use for structure refinement. The QM code typically works with the molecule as with an isolated model in vacuum by the help of localized base. First test of combining the HAR refinement with modelling of the whole periodic system by plane waves and QM DFT calculation was already done as well [3].
The HAR refinement gives primary very different results for hydrogen atom positions. The results are closer to the hydrogen position obtained by neutron diffraction. The reason is a difference between the hydrogen nuclei position and the position of hydrogen related electron density maximum. From this reason we had chosen to test the HAR refinement futures on a salt-cocrystal continuum system for which characterization and proper determination of hydrogen positions is essential.
For the IAM/HAR results comparison we had chosen a set of four quinoline isomeric compounds [4]. The studied structures formula, chemical names and CSD deposition codes are given in Fig. 1. For all these compounds a high-quality low temperature (185 K) Mo Kα data were already available. The system exhibits an interesting salt-cocrystal dynamic hydrogen transfer worth to study.
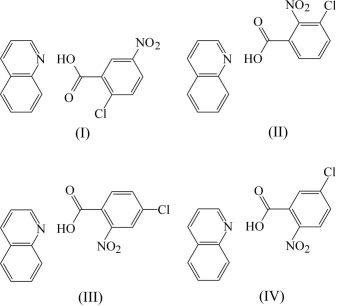
Figure 1. 2-chloro-5-nitrobenzoic acid–quinoline (1/1), (I) AJIWIA , 3-chloro-2-nitrobenzoic acid–quinoline (1/1), (II) AJIWOG, 4-chloro-2-nitrobenzoic acid–quinoline (1/1), (III) AJIWUM, and 5-chloro-nitrobenzoic acid–quinoline (1/1), (IV) AJIXAT.
Methods
The original data from the authors were re-interpreted by the help of Olex2 software and HAR refinement by the NoSpheraA2 module [2]. Tree different refinement setups were used: 1) IAM with hydrogen atoms threaded isotropic 2) HAR with hydrogen atoms threaded isotropic 3) HAR with hydrogen atoms threaded anisotropic (disordered one isotropic). The 1) and 2) refinement setup make possible to compare the R factor for situation with identical number of refined parameters. The QM calculations were done in Orca 5.0 software, cc-pVTZ base, PBE functional. To be able to model a disordered H positions the QM code had calculated for all structures models with hydrogen in both salt and cocrystal position. The refinement handled the structure as disordered between these two models. For all refinements the O-H and N-H distances of disordered hydrogen were restrained to get convergence.
Results
The results are summarized in Tab. 1 and Tab. 2.
Table 1. Comparison of R factors for different refinement methods.
|
Refinement setup |
I, AJIWIA |
II, AJIWOG |
III, AJIWUM |
IV, AJIXAT |
|
IAM original authors, SHELXL97 |
0.033 |
0.037 |
0.037 |
0.035 |
|
IAM re-refinement in Olex2 |
0.032 |
0.037 |
0.037 |
0.035 |
|
HAR re-refinement in Olex2 |
0.016 |
0.024 |
0.025 |
0.024 |
|
HAR re-refinement in Olex2, H-anisotropic |
0.016 |
0.022 |
0.024 |
0.023 |
Table 2. Comparison of the hydrogen atom occupancy (salt N site) : (cocrystal O site)
|
Refinement setup |
I, AJIWIA |
II, AJIWOG |
III, AJIWUM |
IV, AJIXAT |
|
IAM original authors, SHELXL97 |
0:1 |
0.39(3):0.61(3) |
0.47(3):0.53(3) |
0.65(3):0.35(3) |
|
IAM re-refinement in Olex2 |
0.14(3):0.86(3) |
0.25(3):0.75(3) |
0.26(3):0.74(3) |
0.61(3):0.39(3) |
|
HAR re-refinement in Olex2 |
0.143(13):0.857(13) |
0.19(2):0.81(2) |
0.23(2):0.77(2) |
0.62(2):0.38(2) |
|
HAR re-refinement in Olex2, H-anisotropic |
0.085(13):0.915(13) |
0.18(3):0.82(3) |
0.18(2):0.82(2) |
0.51(6):0.49(6) |
The uses of HAR refinement significantly decrease the value of R factor. On the other hand, the uses of HAR refinement have only minor effect on the disordered hydrogen occupancy factor. For II and III a slight occupancy decrease in NH position can be observed probably due to including the nitrogen lone pair in the calculation. There is no significant change in R factor nor in occupancy for the refinement with hydrogen treated anisotropic in comparison to isotopic treatment.
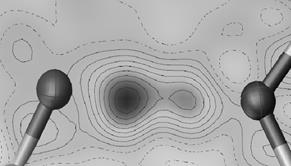

Figure 1. Difference electron density calculation for AJIWUM in the O…H…N region. IAM refinement (left) and HAR refinement (H treated anisotropic) (right).
The difference between IAM and HAR refinement and IAM refinement is even more visible on Fig. 1. The IAM refinement indicates hydrogen in 2 positions. The HAR refinement electron density map corresponds more close to the Path Integral Molecular Dynamic (PIMD) simulation results as calculated for similar situations [5]. The hydrogen is not exactly in 2 positions but instead creates a disordered cloud of electrons between the oxygen and hydrogen atoms.