Investigation of phases from salt-cocrystal continuum using DFT calculations
S. Chalupná (maiden name Šajbanová), M. Hušák
Department of Solid State Chemistry, University of Chemistry and Technology, Prague, Technická 5, Praha 6, 166 28, Czech Republic
sajbanos@vscht.cz
Introduction
A broad range of solid forms available for pharmaceutical molecules exists nowadays. Pharmaceutical salts are one of the forms that can be used for formulation of active components. About 50% of drugs used today are salts. Additionally, cocrystals are rapidly evolving as another prominent type of pharmaceutical form. [1,2] The difference between salt and cocrystal is given only by the position of single hydrogen. As this difference is quite small, it is an essential task to develop new techniques that can accurately identify the precise location of the relevant hydrogen atom. We had already developed and partially tested a computational method for salt cocrystal differentiation based on DFT energy calculation. [1,3]
The DFT method optimizes an artificially constructed wrong structure (hydrogen atom placed in salt position near the potential acceptor for cocrystals and vice versa cocrystal position with hydrogen atom placed near the potential donor of the salts). The verification of the method was done based on comparison of the results with an experimentally confirmed correct hydrogen position on 95 structures. As the data source for testing of the DFT method we used a Cambridge Structural Database (CSD) deposition code list of structures from the zone (-1 ≤ ΔpKa ≤ 4), defined in an article “Acid–base crystalline complexes and the pKa rule”. [4]
In addition to the salt and cocrystal form, we had detected presence of a form which can be described as salt-cocrystal continuum. For such a form the hydrogen can be found in two energetic minima (Fig. 1). The detection and examination of these forms is crucial for ensuring compliance with legal and regulatory standards.
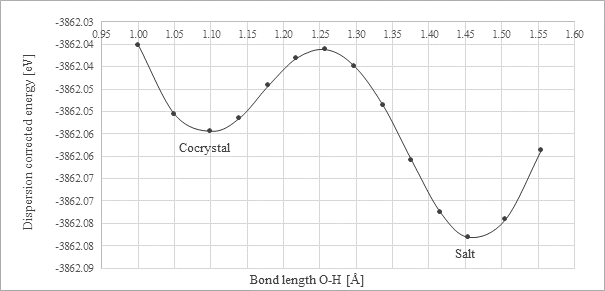
Figure 1. Energy dependence on H atom position for the PUJNIS structure calculated by the PBE+TS functional [1]
In addition, a quantum dynamic simulation was performed to verify that the results of the DFT method correspond to the room temperature state of the crystals.
Methods
The DFT method uses the newest version of Castep 22.11 software. The rSCAN functional in combination with MBD dispersion correction and fine basis precision was used. The data were prepared in BIOVIA Materials Studio software. Computation was performed on Karolina supercomputer at TU Ostrava. The computational power required for calculation of 450 structures was approximately 3 000 core/hours on 128 core nodes.
In addition to simple geometry optimization, we had performed Path Integral Molecular Dynamics (PIMD) simulation for one structure (CSD code AJIWUM). PIMD is a computational simulation method that combines Molecular Dynamics (MD) and description of Nuclear Quantum Effects (NQE). We have used quantum PIMD simulation because the energy was calculated by DFT method. The Path Integral (PI) involves representing the motion of particles as a path of imaginary time slices, which allows the inclusion of NQE effects in MD. PIMD is particularly useful in studying systems with strong NQE effects, such as hydrogen bonding or proton transfer. [5] The PIMD simulation of the studied system was also performed in CASTEP. NVT ensemble, temperature of 150 K, a Langevin thermostat, a 0,5-fs integration time step and a planewave cut-off energy of 571 eV were used. For energy calculation we had used rSCAN functional with MBD dispersion correction again. The path-integral propagation used a Trotter decomposition of all nuclei into 16 beads, which has been shown to be sufficient for simulations of molecular crystals at 300 K. [6]
Results
The results of structures from the zone (-1 ≤ ΔpKa ≤ 4) are summarized in Tab.1. While testing our computational method, we discovered 90 structures that exhibit the above-mentioned two energetic minima. Further investigation of these structures is yet to be conducted.
Table 1. Results of calculation on 418 structures from the zone with -1 ≤ ΔpKa ≤ 4 (RSCAN fine + MBD)
|
Pure cocrystal |
Pure salt |
Salt-cocrystal continuum phase |
|
312 |
16 |
90 |
An additional 30 structures with dual hydrogen position were detected using the 3D search for disordered hydrogen position. In this study we had investigated both salts, cocrystals and solvates. For these structures, the presence of a double hydrogen position had already been detected by the original authors. We proceeded to perform DFT calculations on these structures, using the settings specified above. The results are summarized in Tab. 2.
Table 2. Results of calculation on 30 structures with experimentally detected salt-cocrystal disordered hydrogen (RSCAN fine + MBD)
|
Pure cocrystal or solvate |
Pure salt |
Confirmed salt-cocrystal continuum phase |
|
7 |
7 |
16 |
As a sample of structure described incorrectly based on experiment, we can mention structure with CSD deposition code ILUCIB. It was identified by us as a pure solvate, which differs from the classification given in the original publication. This structure is composed of pyridinium (pKa = 5,23) and 3,3',4-tri-O-methylflavellagate (pKa » 6). [7] That means that ΔpKa = pKa[base] – pKa[acid] = -1, but actual flavonoid salts are formed when ΔpKa is approximately 10. [7] Therefore, we believe that the structure is incorrectly solved, and it cannot be a salt or salt-cocrystal continuum phase. Other incorrect results will be evaluated using the same approach.
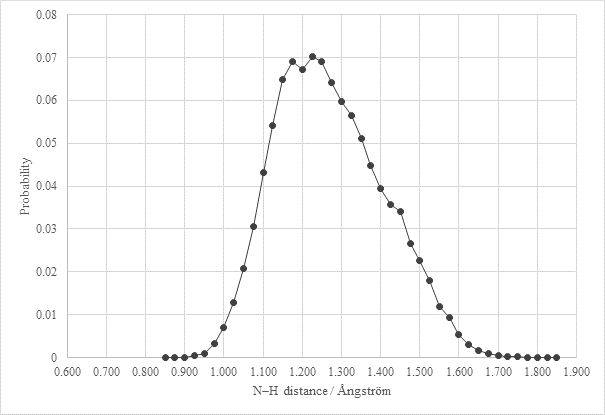
Figure 2. Probability distribution of the N–H distances obtained from PIMD simulation of AJIWUM
For structure with CSD deposition code AJIWUM the Path Integral Molecular Dynamic (PIMD) simulation was performed. In Figure 2 we can see the probability distribution of the N-H (or N…H) distance in AJIWUM system. Results of this simulation reveal that the hydrogen is not precisely located in 2 positions but is delocalized between the donor and the acceptor of the H-bond. Such situation will be probably common for most structures from the salt-cocrystal continuum area at room temperature.
1. Šajbanová, S. Validace metody rozlišení solí a kokrystalů pomocí DFT výpočtu. diplomová práce, Vysoká škola chemicko-technologická v Praze, červen 2022.
2. Kratochvíl, B. KOKRYSTALY A JEJICH OČEKÁVANÉ FARMACEUTICKÉ APLIKACE. Chem. Listy 2010, 104, 823–830.
3. Hušák, M.; Šajbanová, S.; Klimeš, J.; Jegorov, A. The possibilities of salt-cocrystal distinguishing based on dispersion-corrected density functional theory calculations. Acta Crystallographica Section B. 2022, 78, 5, 781 – 788.
4. Cruz-Cabeza, A. J. Acid–base crystalline complexes and the pKa rule. CrystEngComm 2012, 14, 6362–6365.
5. R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals (McGraw-Hill, New York, 1965).
6. Štoček JR, Socha O, Císařová I, Slanina T, Dračínský M. Importance of Nuclear Quantum Effects for Molecular Cocrystals with Short Hydrogen Bonds. J Am Chem Soc. 2022 Apr 27;144(16):7111-7116. doi: 10.1021/jacs.1c10885. Epub 2022 Apr 8. PMID: 35394771.
7. Elisabet Fuguet, Clara Ràfols, Meritxell Mañé, Rebeca Ruiz, Elisabeth Bosch, Acidity constants of hydroxyl groups placed in several flavonoids: Two flavanones, two flavones and five flavonols,Talanta,Volume 253,2023,124096,ISSN 0039-9140,https://doi.org/10.1016/j.talanta.2022.124096.