X-ray diffraction analysis of epitaxial layers with depth-dependent composition

E. Dobročka

Institute of Electrical Engineering, Slovak Academy of Sciences, Dúbravská cesta 9,841 04 Bratislava, Slovak Republic

edmund.dobrocka@savba.sk

High resolution mode is a special branch of X-ray diffraction techniques devoted to the analysis of single crystalline epitaxial layers. One of the most important tasks in epitaxial technologies is the determination of the layer composition. For epitaxial systems with high degree of perfection, e. g. Si- or GaAs-based compounds, the recorded diffraction curves have rather complex form and the layer parameters are routinely determined by computer simulation of the model structure. For epitaxial layers based on materials with lower quality and/or larger lattice mismatch, the fine features of the diffraction curves are missing and only more or less separated diffraction maxima of individual layers can be observed. Typical examples of such materials are the III–nitride semiconductors as AlN, GaN, InN and their ternary alloys. These materials have great potential for use in optoelectronic and high-temperature electronic devices due to their wide range of bandgaps and high-temperature stability [1-3].

If the layers are perfectly matched to the substrate, it is sufficient the measuring of one symmetric diffraction of the type . But in the case of layers exhibiting certain degree of relaxation, in addition to the symmetric diffraction, at least one asymmetric diffraction has to be measured. From the position of the diffraction spots the composition as well as the degree of relaxation can be determined. For the GaN based compounds the most convenient and accessible asymmetric diffraction is . There are six equivalent diffractions of this type in hexagonal materials but if the lattice tilting does not take place, it is, in principle, sufficient to measure only one of these diffractions. However, measuring of several diffractions increases the precision of the evaluation. Further simplification stems from the symmetry of the stress state of the layer. Hexagonal c-oriented epitaxial layers are transversely isotropic, i.e. the deformation of the layer is completely described by two nonzero strain components:

(1)

where and , are the lattice parameters of strained (and measured) and fully relaxed layer, respectively [4]. These components are connected by the relation

(2)

where and are the composition dependent stiffness constants of the material. Alternatively, instead of in-plane strain , the degree of relaxation defined as

(3)

is often used to describe the strain state of the epitaxial layer. It has to be pointed out that the parameter characterizes the strain state of the layer with respect to the substrate lattice.

The values of and can be calculated from the reciprocal co-ordinates and of the layer diffraction spot as [5]

(4)

The unknown composition parameter and the in-plane strain can be obtained by solving the system of equations in (1) and (2). A simple iterative procedure that uses and in (4) as input parameters is outlined in [6]. The method supposes linear dependence of the parameters , and , on the composition .

The complete information on the state of the epitaxial layer can be obtained by measuring the reciprocal space map (RSM) around a suitable asymmetric diffraction. For the later purposes it is reasonable to introduce the presentation of the admissible positions of the layer spots in reciprocal space in dependence of the layer composition and the degree of relaxation. It follows from simple geometrical considerations that in the case of AlGaN/GaN and InGaN/GaN systems the possible positions of the layer diffraction spot are confined to triangular region in the vicinity of GaN diffraction. This area is bounded by the so called relaxation line connecting the AlN or InN layer diffraction spots for fully strained and completely relaxed state [7]. The third vertex of the triangle is the GaN substrate (or buffer layer) diffraction spot. However, for the system InAlN/GaN this area comprises two triangular regions as shown in Fig. 1. This is a consequence of the fact that the lattice parameters of GaN are in between the parameters of InN and AlN lattices. The common vertex of these triangles corresponds to the composition of the In_xAl_1-xN for which the layer is perfectly matched to the GaN lattice. It is worth noting that this point in reciprocal space does not coincide with the GaN diffraction spot. This is a general property of hexagonal epitaxial systems and it stems from different values of aspect ratios of In_xAl_1-xN and GaN lattice.

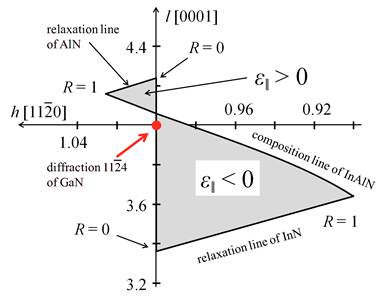
Figure 1. Schematic drawing of the admissible positions of the diffraction spot of InAlN layer for various composition 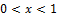and degree of relaxation 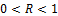. Note the sign of the in-plane strain component 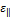is opposite in Al rich and In rich regions. For the sake of clarity the width of the area is 6-times enlarged.

If In_xAl_1-xN layer is grown on GaN buffer layer in sequence (without breaking the growth after GaN), unintentional Ga-auto-incorporation into In_xAl_1-xN layer is an obvious problem, as reported in [8-10]. Sources of Ga could be the deposited Ga-containing-residues on the reactor wall, susceptor or shower head during GaN growth. Due to the Ga-incorporation in InAlN, intended In_xAl_1-xN ternary alloy actually becomes In_xAl_yGa_1-x-yN quaternary alloy. This has a significant consequence for the evaluation of X-ray diffraction measurements, e. g. for the interpretation of the RSM. In the case of ternary compounds each couple of lattice parameters a and c of strained layer measured by X-ray diffraction has a unique solution , , and . Evidently, this is not valid for quaternary compounds. In this case the composition of the layer is described by two parameters, e. g. In_xAl_yGa_1-x-yN, and the measured values of strained lattice parameters and can be interpreted by an infinite number of , values resulting in different relaxed lattice parameters , and different degree of in-plane strain . As an illustration, in Tab. 1 five different compositions of quaternary In_xAl_yGa_1-x-yN layer resulting in the same values of measured lattice parameters are listed.

Table 1. Five compositions of quaternary In_xAl_yGa_1-x-yN layer for the same values of measured lattice parameters and corresponding relaxed lattice parameters , and in-plane strain component .

Ga [%]	In [%]	Al [%]	[nm]	[nm]	[%]
0.0	18.4	81.6	0.31898	0.51134	– 0.14
5.0	17.2	77.8	0.31884	0.51147	– 0.09
10.0	16.0	74.0	0.31870	0.51160	– 0.05
15.0	14.7	70.3	0.31856	0.51173	– 0.006
20.0	13.5	66.5	0.31843	0.51187	0.04

This example clearly demonstrates that in the case of quaternary compounds the X-ray measurements alone are insufficient for the determination of the layer composition and further independent analytical technique is required for the evaluation of the structural parameters of the layer. Moreover, the concentration of Ga atoms in the In_xAl_1-xN layer is strongly dept-dependent with higher value at the bottom close to the GaN buffer layer. The depth distribution of the elements in the quaternary layer can be determined e. g. 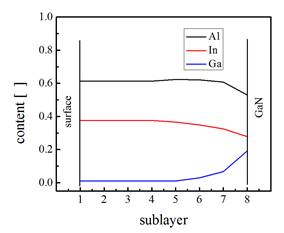by Rutherford backscattering spectrometry (RBS), X-ray photoelectron spectroscopy etc. An example of depth profile of the layer composition obtained by RBS measurement is given in Fig. 2. It is seen that the highest concentration, almost 20%, of Ga is at the bottom of the layer and from the middle up to the layer surface the Ga content is negligible. The distance between the adjacent sublayers is ~ 40 nm. The total layer thickness is ~280 nm. These measurements can be combined with the X-ray results in the way outlined in the following.

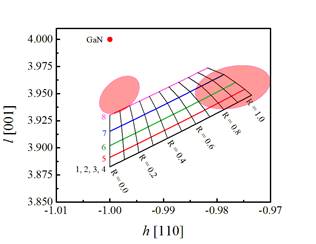
Figure 2. Depth profile of InAlGaN layer composition. The distance between the adjacent sublayers is ~ 40 nm.	Figure 3. Composition & Relaxation diagram of InAlGaN layer. The position of two maxima revealed by X-ray RSM are schematically shown as ellipses.

The data describing the depth distribution of the elements in the layer are used as input parameters and the theoretical relaxation lines are calculated for all sublayers with their particular composition obtained by RBS analysis. The set of calculated relaxation lines plotted in reciprocal space build up a special mesh – the composition & relaxation diagram. Each relaxation line in this diagram is connected with a sublayer in different depth, hence at favourable circumstances the eventual depth distribution of the relaxation can be established simply by comparison of the diagram with the measured RSM (not shown here). Such a comparison is given in Fig. 3.

It is seen that in addition to the basic GaN diffraction two distinct but rather broad maxima corresponding to epitaxial layer were revealed. They are schematically depicted in the diagram as transparent red ellipses. The curves of constant degree of relaxation are also shown. It can be concluded that the InAlN layer with incorporated Ga atoms is apparently divided into two layers. The maximum on the left side can be ascribed to the bottom layer with high Ga content. The layer is almost perfectly matched to the GaN buffer layer. It is also evident that the Ga content provided by RBS measurement is somewhat underestimated, the maximum does not lie on the deepest relaxation line having the highest Ga content. The right side maximum can be related to the upper layer with negligible Ga content. The layer is almost fully relaxed.

1. J. Kuzmík, IEEE Electron Device Lett., 22, (2001), 510.

2. Y. Yue, Z. Hu, J. Guo, B. Sensale-Rodriguez, G. Li, R. Wang, F. Faria, T. Fang, B. Song, X. Gao, IEEE Electron Device Lett., 33, (2012), 988.

3. J. Kuzmík, A. Georgakilas, IEEE Trans. Electron Dev., 58, (2011), 720.

4. A. Krost, A. Dadgar, G. Strassburger, R. Clos, phys. status solidi A, 200, (2003), 26.

5. E. Dobročka, S. Hasenöhrl, P. Chauhan, J. Kuzmík, Appl. Surf. Sci. 461, (2018), 23.

6. P. Chauhan, S. Hasenöhrl, E. Dobročka, Ľ. Vančo, R. Stoklas, J. Kováč, P. Šiffalovič, J. Kuzmík, Appl. Surf. Sci. 470, (2019), 1.

7. U. Pietsch, V. Holý, T. Baumbach, High-Resolution X-Ray Scattering, second ed., Springer, New York, 2004.

8. S. Choi, H. J. Kim, Z. Lochner, J. Kim, R. D. Dupuis, A. M. Fischer, Yu. R. Juday, T. L. Huang, J. Y. Huang, F. A. Ponce, J.-H. Ryou, J. Cryst. Growth, 388, (2014), 137.

9. J. Kim, Z. Lochner, M.-H. Ji, S. Choi, H. J. Kim, J. S. Kim, R. D. Dupuis, A. M. Fischer, Yu. R. Juday, T. L. Huang, J. Y. Huang, F. A. Ponce, J.-H. Ryou, J. Cryst. Growth, 388, (2014), 143.

10. M. Hiroki, Y. Oda, N. Watanabe, N. Maeda, H. Yokoyama, K. Kumakura, H. Yamamoto, J. Cryst. Growth, 382, (2013), 36.

The author gratefully acknowledges S. Hasenöhrl for providing the sample and D. Machajdík for RBS measurement.