Measuring of residual stresses in strongly textured thin films
E. Dobročka1, P. Novák2, D. Búc3
1Institute of Electrical Engineering, Slovak Academy of Sciences, Dúbravská cesta 9,841 04 Bratislava, Slovak Republic
2Institute of Nuclear and Physical Engineering, Faculty of Electrical Engineering and Information Technology, Slovak University of Technology, Ilkovičova 3, 812 19 Bratislava, Slovak Republic
3Institute of Electronics and Photonics, Faculty of Electrical Engineering and Information Technology, Slovak University of Technology, Ilkovičova 3, 812 19 Bratislava, Slovak Republic
edmund.dobrocka@savba.sk
The presence of
residual stresses in the near surface region of bulk materials and in thin
films is a general problem of various technologies. Among a number of methods
developed for stress analysis, X-ray diffraction methods are of special
importance due to their capability to analyze the depth variation of the
residual stresses. Since the first stress determination by X-ray diffraction in
the 1930s a large variety of measuring methods and evaluation procedures were
developed. While the standard 
method can be easily used for bulk materials, it is not applicable
for thin films, where steep stress gradient perpendicular to the sample surface
can be present. In this case the methods based on grazing incidence (GI) set-up
are more appropriate. The constant (and usually small) angle of incidence α,
that is a characteristic feature of GI X-ray diffraction, ensures that the
information depth does not change during the measurement. The GI method of
stress determination is classified as multiple {hkl} mode in comparison
with the method, that uses only one set of {hkl} planes while the
angle of sample inclination χ varies. The GI method is based on the fact
that all diffraction vectors contributing to the GI diffraction pattern make
different angles with the surface normal of the sample and provide sufficient
set of data for stress evaluation. However, this method of stress measurement
fails if the analyzed layer is strongly textured. In this case the orientation
of the diffraction vectors is sharply localized and the number of diffractions
registered in the measurement performed at constant α and χ
(usually 
) may be insufficient for the evaluation of the stress state.
In the presented
contribution a modified method combining multiple {hkl} and multiple χ
modes of stress measurements is outlined. Measuring at 
can significantly increase the number of accessible diffractions. The
analyzed film is supposed to have a fibre texture with the texture axis 
parallel to the surface normal. The most probable values of angles ψ
between the diffraction vectors and the direction are calculated from single crystal data. In order to measure the
diffraction with Bragg angle θ at selected angle of incidence α, the tilting angle χ and the rotation angle ω of the
goniometer have to be calculated according to relations
and
Due to rotational symmetry of the texture there is no specific restriction for the azimuthal angle ϕ.
The described
method was used for evaluation of biaxial stress in ZnO layers deposited on
(111) GaP substrates. The stress measurements were performed on as deposited
samples and repeated after annealing at 300 °C for 1 hour in N2
atmosphere. The details of sample preparation are given elsewhere [1]. The
layers exhibit strong fibre texture with [001] axis perpendicular to sample
surface, the 002 pole figure is shown in Fig. 1. Due to this texture, only
three diffractions (002, 103 and 203) with sufficient intensities can be used
for stress evaluation, when the diffraction pattern is recorded in standard GI
set-up with 
and . However, polycrystalline
hexagonal ZnO provides 20 diffractions in the range 
(for Cu Kα radiation) with relative intensities above 1%, 17
of them are accessible by an appropriate choice of angles χ and ω
for a constant angle of incidence . Ten strongest diffractions were measured for different values of ψ
around the ideal angle corresponding to single crystal data.
|
|
|
Figure 1. 3D Pole figure 002 of ZnO layer measured within the angular range χ = 0° - 30°. |
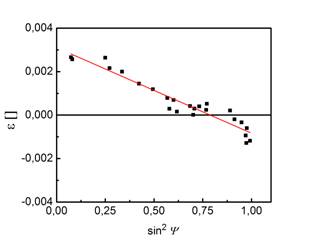
Figure 2. sin2ψ plot based on the combination of multiple hkl and multiple χ mode of stress measurement. |
The results for
annealed sample are collected in standard plot in Fig. 2. It
is seen that the points cover almost uniformly the whole range of the parameter
. The crystallite group method proposed for thin films with fibre
texture [2] was employed for the calculation of biaxial stress. The appropriate
relation for hexagonal crystals with this type of texture has the form
It was found that the stress in ZnO layers is compressive and its value decreased significantly upon annealing from 3 GPa to 0.5 GPa.
The method
enables to analyze also the depth variation of the stress by changing the angle
of incidence α. However, approaching the critical angle for total
external reflection, an appropriate correction of measured diffraction angles
has to be made. In addition, for inclined geometry () the plane of refraction does not coincide with the diffraction
plane and the standard corrections have to be modified [3]. Further
improvements can be achieved by applying more sophisticated models developed
for thin films [4].