Accuracy of structure analysis of single nanocrystals by PEDT

C. A. Corrêa^1,2, L. Palatinus¹, M. Klementová¹

¹Department of Structure Analysis, AS CR, Cukrovarnická 10/112, Prague- Czech Republic

²Department of Physics of Materials, Charles University Prague, Ke Karlovu 5, Prague – Czech Republic

cinthiacac@gmail.com

The development and improvement of nanomaterials require the accurate structure analysis of single nanocrystals. Electron diffraction (ED) allows the structure analysis of single nanocrystals as small as tens of nanometers thanks to the strong interaction between electrons and matter, compared to X-rays, and has already been used for some time for this purpose [1-4]. The three-dimensional information of the reciprocal space may be obtained by using electron diffraction tomography (EDT) [5,6], which consists of tilting the crystal in small steps around the axis of the goniometer and collecting a diffraction pattern at each position. Because the angular position between the patterns is known, the three-dimensional information of the reciprocal space can be reconstructed. However, multiple scattering of the beam cannot be neglected for ED. One remedy to these dynamical interactions is to use precession electron diffraction (PED) [7,8], where the beam is precessed around the optical axis of the microscope, making a cone surface with the vertex at the sample. The beam is deflected back to the optical axis after passing through the sample, resulting in reflection spots in the pattern (Fig. 1). PED data sets have the intensities integrated over all the positions of the beam during the precession, resulting in intensities less sensitive to multiple scattering effects and crystal defects and more sensitive to structure parameters. Several structures of nanocrystalline materials of diverse complexity have been determined using precession electron diffraction tomography (PEDT) [9-11]. Despite of giving reliable structure solution, the use of kinematical approximation is not suitable for the least-squares structure refinement against ED data. Such refinement results in higher figures of merit and lower accuracy of structure parameters. To properly account for the dynamical character of electron diffraction, the dynamical theory of diffraction should be used. The usefulness of the dynamical refinement for PEDT data was recently demonstrated [12,13] and it was shown to give more accurate structure parameters and lower figures of merit when compared to refinements using the kinematical approximation. In this work, the comparison of the kinematical and the dynamical refinements with the reference structure obtained by single crystal X-ray diffraction is presented for 5 samples. The comparison is performed between the standard crystallographic residue parameters R1(obs), wR(all), average distance from the reference atomic position (ADRA) and maximal distance from the reference atomic position (MDRA). It is shown that the PEDT model refined using the dynamical theory of diffraction matches very well with the reference structure, with lower figures of merit and an average distance from the reference atom (ADRA) lower than 0.021 Å (Tab. 1).

 

 

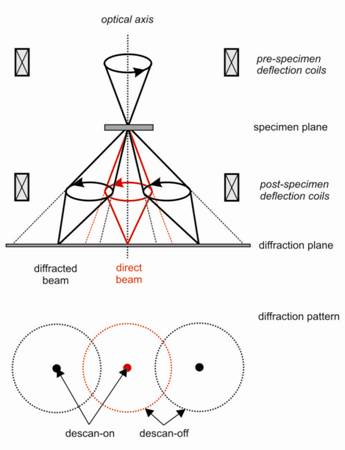
Figure 1. During the precession electron diffraction, the beam is deflected from the optical axis of the microscope, making a cone surface with the vertex at the sample. The post-specimen coils deflect the beam back, resulting in a diffraction pattern with spots instead of circles.

 

Table 1. Samples used in the comparison of the dynamical refinement against the reference structure and the kinematical refinement.

1. B. K. Vainshtein, Electron Diffraction Structure Analysis. New York: Plenum Press. 1964.

2. J. M. Cowley, Electron Diffraction Techniques, Vols 1 and 2. Oxford University Press. 1992.

3. D. L. Dorset, Structural Electron Crystallography, New York: Plenum Press. 1995.

4. U. Kolb, T. Gorelik, E. Mugnaioli, Materials Research Society Symposium Proceedings, 1184, (2009).

5. U. Kolb, T. Gorelik, C. Kuebel, M. T. Otten, D. Hubert, Ultramicroscopy, 107, (2007), 507.

6. U. Kolb, T. Gorelik, M. T. Otten, Ultramicroscopy, 108, (2008), 763.

7. R. Vincent, P. A. Midgley, Ultramicroscopy, 53, (1994), 271

8. E. Mugnaioli, T. Gorelik, U. Kolb, Ultramicroscopy, 109, (2009), 758.

9. D. Jacob, P. Cordier, Ultramicroscopy, 110, (2010), 1166.

10. L. Palatinus, M. Klementová, V. Dřínek, M. Jarošová, V. Petříček, Inorganic Chemistry, 50, (2011), 3743.

11. U. Kolb, E. Mugnaioli, Microporous and Mesoporous Materials, 189, (2014), 107.

12. L. Palatinus, J. Damien, P. Cuvillier, M. Klementová, W. Shinkler, L. D. Marks, Acta Cryatallographica, A69, (2013), 171.

13. L. Palatinus, V. Petříček, C. A. Corrêa, Acta Crystallographica, A71, (2015), 235.

 

This project is financially supported by the Czech Science Foundation, project number 13-25747S.