Využití Fourierovy transformace při obrazové analýze mikrofotografií

M. Šlouf, T. Vacková

Ústav makromolekulární chemie AV ČR, v.v.i., Heyrovského nám. 2, 16206 Praha 6

slouf@imc.cas.cz

Fourierova transformace (FT) je jedním z pokročilých nástrojů, které lze využít při obrazové analýze mikrofotografií, neboli při „převodu obrázků na čísla“. V tomto příspěvku velmi stručně shrneme teorii FT, která souvisí se zpracováním mikrofotografií. Přitom se soustředíme na metody výpočtu a interpretace FT pro tři nejčastější případy v obrazové analýze: (i) jednorozměrnou diskrétní rychlou FT (1D-DFFT) čárových profilů intenzit, (ii) dvourozměrnou diskrétní rychlou FT (2D-DFFT) vybraných ploch a (iii) převod vypočtených 2D-DFFT na 1D radiální profily.

Pomocí FT můžeme z LM, SEM, TEM) získat informace o periodických vzdálenostech a symetrii struktury v mikroskopické škále (stovky mikrometrů – jednotky nanometrů). Pro výpočty potřebujeme dostatečně flexibilní programy, které umožní obrázky upravovat, vybírat z nich čárové profily a/nebo oblasti a následně počítat různé typy FT. V této práci využíváme dvou volně šiřitelných programů: ImageJ [1] na manipulaci s obrázky a programovací jazyk Python [2] s příslušnými moduly [3, 4] na výpočty FT.

Schéma na obrázku 1 ukazuje využití 2D-DFFT pro potvrzení šesterečné symetrie a periodicity ve vzorku blokového kopolymeru P(MMA-co-GMA)-b-PMAPOSS [5]. Ze vzorku byl připraven ultratenký řez, který byl po kontrastování v parách RuO₄ zobrazen v TEM. Nízkoúhlový rozptyl paprsků X (SAXS) naznačoval, že by polymer měl vykazovat hexagonální strukturu. V některých oblastech TEM mikrofotografií byla hexagonální struktura zčásti patrná (obr. 2a), ale kontrast byl velice malý a ani úpravy v programu ImageJ příliš nepomohly (obr. 2b). Proto byl vybraný obrázek v ImageJ binarizován, v programu Python vypočtena 2D-DFFT (obr. 2c) a následně i 1D radiální distribuce (obr. 2d). Symetrie 2D-DFFT obrazu jasně potvrdila hexagonální symetrii, zatímco z 1D radiální distribuce bylo možno vypočítat průměrnou vzdálenost mezi hexagonálně uspořádanými sloupci (d = 18 nm), která byla ve shodě s výsledky SAXS (d = 20 nm).

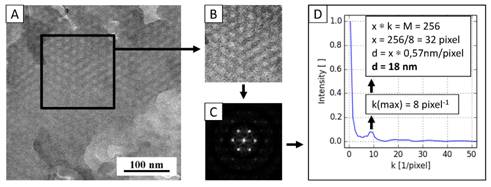
Obrázek 1. Potvrzení hexagonální struktury v P(MMA-co-GMA)-b-PMAPOSS: (a) TEM mikrofotografie, (b) vybraná oblast (c) 2D-DFFT z vybrané oblasti, 4x zvětšeno a (d) 1D radiální profil s výpočtem vzdálenosti d mezi sloupci.

V přednášce ukážeme ještě řadu dalších případů z praxe, včetně (překvapivě jednoduchých a krátkých) zdrojových kódů v jazyce Python pro uživatelsky definované výpočty FT z mikrofotografií.

1. Domovská stránka programu ImageJ: http://imagej.nih.gov/ij/

2. Hlavní stránka programovacího jazyka Python: https://www.python.org/

3. Distribuce WinPython, obsahující moduly pro čtení/zápis obrázků a výpočty FT: http://winpython.sourceforge.net/

4. Modul radial_data.py: http://www.astrobetter.com/fourier-transforms-of-images-in-python/

5. L. Matějka, M. Janata, J. Pleštil, A. Zhigunov, M. Šlouf, Polymer 55, (2014), 126.

TAČR TE01020118, GAČR P108/14-17921S.