Využití Fourierovy
transformace při obrazové analýze mikrofotografií
M. Šlouf, T. Vacková
Ústav makromolekulární chemie AV ČR, v.v.i., Heyrovského nám. 2, 16206 Praha 6
slouf@imc.cas.cz
Keywords: Fourier transform, microscopy, image analysis, ImageJ, Python
Abstract
Fourier transform (FT) is one of advanced tools for image analysis of micrographs. In this contribution, we briefly summarize FT theory associated with image analysis, namely the calculation and interpretation of (i) one-dimensional discrete fast FT (1D-DFFT) of line intensity profiles, (ii) two-dimensional discrete fast FT (2D-DFFT) of selected areas and (iii) transformation of 2D-DFFT images to 1D radial profiles. On numerous examples, we show how FT analysis reveals periodicity, symmetry and asymmetry of micro- and nanostructured materials. Other connections between FT and microscopy, such as maximum resolution of light microscopes, theory of imaging and calculation of light and electron diffraction patterns are mentioned. We demonstrate that FT is not only useful, but also beautiful method of image analysis.
Úvod
Fourierova transformace
(FT) je jedním z pokročilých nástrojů, které lze využít při obrazové
analýze mikrofotografií, neboli při „převodu obrázků na čísla“. V tomto
příspěvku velmi stručně shrnujeme teorii FT, která souvisí se zpracováním
mikrofotografií. Přitom se soustředíme na metody výpočtu a interpretace FT pro
tři nejčastější případy v této oblasti: (i) jednorozměrnou diskrétní
rychlou FT (1D-DFFT) čárových profilů intenzit, (ii) dvourozměrnou diskrétní
rychlou FT (2D-DFFT) vybraných ploch a (iii) převod vypočtených 2D-DFFT na 1D
radiální profily. Na příkladech demonstrujeme, jak může FT pomoci zviditelnit
periodické vzdálenosti, symetrii a asymetrii v mikro- a nanostruktuře materiálů.
Stručně též zmiňujeme další souvislosti mezi FT a mikroskopií, jako je
maximální rozlišení světelných mikroskopů, teorie zobrazení a interpretace
difraktogramů.
Materiály, mikroskopické metody a výpočty FT
Materiály a mikroskopické
preparáty použité v této práci byly zakoupeny a/nebo připraveny na
pracovišti autorů v průběhu posledních 10–15 let. Použité experimentální
metody zahrnují světelnou mikroskopii (LM), rastrovací elektronovou mikroskopii
(SEM) a transmisní elektronovou mikroskopii (TEM). Vzorky, jejich příprava a
vlastní mikroskopie nejsou detailně popisovány, ale v případě potřeby jen
stručně zmíněny u jednotlivých příkladů přímo v textu.
Pro zpracování
mikrofotografií a/nebo výpočty FT existuje řada komerčních i volně šiřitelných
programů. V této práci jsme použili dva volně šiřitelné programy:
interaktivní program pro zpracování (mikro)fotografií ImageJ [1] a
interpretovaný programovací jazyk Python [2].
ImageJ je víceúčelový
program, který dokáže při zpracování obrazu věci jednoduché (převody obrazových
formátů, úpravy jasu, kontrastu, gamma; kalibrace, interaktivní měření
vzdáleností a ploch aj.) i složitější (jako je například zobrazení a uložení
čárových profilů intenzity a výpočty 2D-DFFT).
Zde jsme program použili pro
předběžnou úpravu mikrofotografií, získání intenzitních profilů a kontrolní
výpočty FT (finální výpočty FT byly provedeny v Pythonu, jak je popsáno
dále).
Python je moderní
interpretovaný programovací jazyk vysoké úrovně. Je o něco pomalejší než
standardní kompilované programovací jazyky typu Fortran, C nebo C++, ale má
rozsáhlé, dobře dokumentované, volně šiřitelné knihovny rychlých podprogramů pro
širokou škálu vědeckých aplikací, včetně obrazové analýzy. V této práci
využíváme knihovny pro čtení/zpracování/zápis obrázků (modul Pillow), převedení
obrázků na rychlá pole (modul NumPy), výpočet jednorozměrné či dvourozměrné FT
(1D-DFFT a 2D-DFFT) z vybrané oblasti (modul SciPy), převod 2D-DFFT obrazů
na 1D-radiální profily (modul radial_data.py) a zobrazení výsledků ve formě
grafů (modul Matplotlib). V přednášce také ukážeme, jak lze Python využít
i k přímým/symbolickým výpočtům FT (modul SymPy). Všechny uvedené moduly
jsou standardní součástí mnoha volně šiřitelných distribucí Pythonu, například
distribuce WinPython [3]; jedinou výjimkou je modul radial_data.py, jehož
zdrojový kód je nutno stáhnout z internetu zvlášť [4].
Základní teorie FT související s obrazovou analýzou
Využití FT při obrazové
analýze zahrnuje zejména tři typy výpočtů, které byly zmíněny již v úvodu:
(i) 1D-DFFT čárových profilů intenzity, (ii) 2D-DFFT
vybraných oblastí a (iii) převod 2D-DFFT obrazů na 1D radiální profily. 1D-DFFT
a 2D-DFFT se počítají podle rovnic (1, 2):
|
|
(1) |
|
|
(2) |
kde (x, y) jsou x-ová a y-ová
souřadnice pixelu v obrázku a I(x,y)
je intenzita v místě daném souřadnicemi [x,y]. Koeficienty (k, l)
udávají souřadnice pixelu v transformovaném obrázku a Akl je (komplexní) amplituda v místě
daném koeficienty [k,l]. V případě jednorozměrných
čárových profilů jde samozřejmě jen o souřadnici x, koeficient k,
intenzitu I(x) a amplitudu Ak.
Intenzity lze získat stejně jako v teorii difrakce jako absolutní hodnoty
čtverců amplitud (Ikl = |Akl|2). Radiální profily intenzit se počítají
z 2D-DFFT obrazů numericky, a to radiálním zprůměrováním hodnot Ikl tak, že dostáváme
jednorozměrnou funkci intenzity I(r), kde r je vzdálenost od středu 2D-DFFT obrazu (názorný příklad viz
následující sekce, obr. 2).
Obrazová analýza s využitím FT: příklady z praxe
První příklad (obr. 1)
ukazuje využití jednorozměrné rychlé diskrétní Fourierovy transformace
(1D-DFFT) pro určení periodicity ve vzorku blokového kopolymeru polystyren-b-poly(styren-co-akrylonitryl)
s lamelární strukturou (polymer PS-b-SAN; [5]). Z kusového vzorku byl
nejprve připraven ultratenký řez (tloušťka 50 nm) pomocí ultramikrotomie
(diamantový nůž, chlazení kapalným dusíkem). Jednotlivé složky byly odlišeny
pomocí kontrastování v parách RuO4 a struktura byla zobrazena
pomocí TEM (obr. 1a). Z TEM mikrofotografie byl získán čárový profil
intenzity signálu napříč lamelami pomocí programu ImageJ (obr. 1b). Ze
zmíněného profilu byla pomocí skriptu v programu Python vypočtena 1D-FFT
(obr. 1c,d), přičemž hlavní frekvence v FT obrazu odpovídala 0,041 nm-1,
což po přepočtu dalo průměrnou periodickou vzdálenost mezi lamelami d = 1/0,041 = 24 nm, která byla ve velmi
dobré shodě s teoretickou předpovědí.
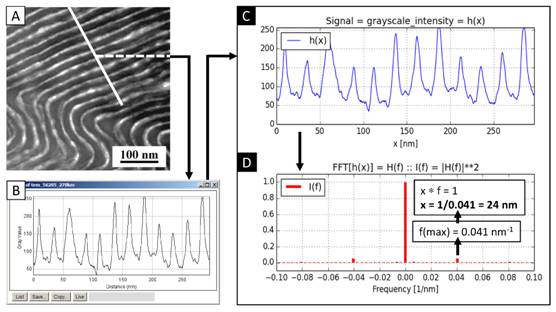
Obrázek 1. Určení periodicity lamel v PS-b-SAN: (a) TEM mikrofotografie, (b) čárový profil intenzity v programu ImageJ a (c, d) výstup ze skriptu v programu Python – načtený profil, jeho 1D-DFFT a výpočet periodické vzdálenosti.
Druhý
příklad (obr. 2) demonstruje využití dvourozměrné rychlé diskrétní Fourierovy
transformace (2D-DFFT) pro názorné potvrzení šesterečné symetrie ve vzorku
blokového kopolymeru P(MMA-co-GMA)-b-PMAPOSS [6]. Ze vzorku byl opět připraven
ultratenký řez, který byl po kontrastování zobrazen na TEM, analogicky jako
v předchozím příkladu. Nízkoúhlový rozptyl paprsků X (SAXS) naznačoval, že
by polymer měl vykazovat hexagonální strukturu. V některých oblastech TEM
mikrofotografií byla hexagonální struktura zčásti patrná (obr. 2a), ale
kontrast byl velice malý a ani úpravy v programu ImageJ příliš nepomohly
(obr. 2b). Proto byl vybraný obrázek v ImageJ binarizován, v programu
Python vypočtena 2D-DFFT (obr. 2c) a následně i 1D radiální distribuce (obr. 2d).
Symetrie 2D-DFFT obrazu jasně potvrdila hexagonální symetrii, zatímco z 1D
radiální distribuce bylo možno vypočítat průměrnou vzdálenost mezi hexagonálně
uspořádanými sloupci (d = 18 nm), která byla ve shodě s výsledky SAXS (d =
20 nm).
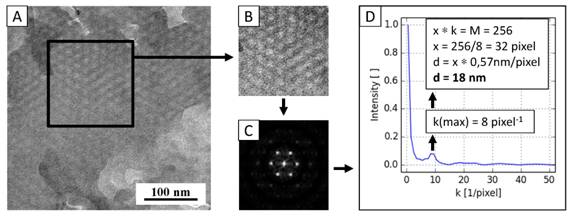
Obrázek 2. Potvrzení hexagonální struktury v P(MMA-co-GMA)-b-PMAPOSS: (a) TEM mikrofotografie, (b) vybraná oblast (c) 2D-DFFT z vybrané oblasti, 4x zvětšeno a (d) 1D radiální profil s výpočtem vzdálenosti d mezi sloupci.
Další příklady, které
budou ukázány v přednášce, zahrnují zejména: (a) modelové symbolické
výpočty FT pomocí Python/SymPy, jejichž výsledkem jsou přímo transformované
funkce, (b) modelové numerické výpočty FT pomocí Python/NumPy demonstrující
vztah mezi frekvencemi v FT obrazech a periodickými vzdálenostmi na
mikrofotografiích, spolu s ukázkami zdrojových kódů programů, které jsou
překvapivě krátké a jednoduché, (c) další ukázky praktického využití FFT
v obrazové analýze jako je hledání periodicity na LM mikrofotografiích
hydrogelů, korekce nesymetrie způsobené astigmatismem v SEM, potvrzení periodického
samouspořádání na TEM mikrofotografiích nanočástic, analýza periodického
uspořádání lamel v polyethylenu a na závěr (d) zmíníme i několik dalších
souvislostí mezi FT a mikroskopií (maximální rozlišení, teorie zobrazování,
analýza difraktogramů).
Závěr
Fourierova transformace
je jedním z nástrojů obrazové analýzy. Hlavním cílem obrazové je
extrahovat číselné informace z obrázků, v našem případě ze světelných
a elektronových mikrofotografií. FT se nevyužívá příliš často, ale při vhodném
použití poskytuje cenné kvantitativní informace a navíc elegantní, názorné
výstupy. V tomto příspěvku jsme stručně popsali uživatelsky definovatelné,
flexibilní metody výpočtu FT pomocí programovacího jazyka Python, nastínili
základní teorii FT související s analýzou obrazu a uvedli několik příkladů
z praxe. V souhrnu můžeme konstatovat, že FT analýza mikrofotografií
slouží k charakterizaci periodických vzdáleností a symetrie uspořádání
materiálů v mikroskopické škále (stovky mikrometrů – jednotky nanometrů).
Literatura
1. Domovská stránka programu ImageJ: http://imagej.nih.gov/ij/
2. Hlavní stránka programovacího jazyka
Python: https://www.python.org/
3. Hlavní stránka distribuce WinPython, včetně modulů: http://winpython.sourceforge.net/
4. Modul radial_data.py: http://www.astrobetter.com/fourier-transforms-of-images-in-python/
5. D. Gromadzki, J. Lokaj, M. Šlouf, P. Štěpánek, Polymer 50, (2009), 2451.
6. L. Matějka, M. Janata, J. Pleštil, A. Zhigunov, M. Šlouf, Polymer 55, (2014), 126.
Acknowledgements.
TAČR TE01020118,
GAČR P108/14-17921S.