Breaking the problem complexity limits for powder diffraction based structure solution

M. Hušák

Institute of Chemical Technology Prague, Technická 5,166 28 Praha 6

husakm@vscht.cz

It can be predicted from theoretical calculations, how much complex structure can be solved from powder diffraction data [1]. The theoretical limit for perfect synchrotron data is about 300 DOF (degree of freedom) while current existing record solves only 42 DOF problem simplified by heavy atom presence [2]. We have tried to determine a realistic DOF limit based on perfect simulated powder diffraction data. For the simulation we have chosen peptide structures from CSD: 1 single peptide molecule in asymmetric unit cell, 2-8 amino acids, 10-39 DOF. The parameters of the simulated powder diffractogram used were close to typical perfect measurement on ID31 of ESRF - wavelength 0.5 Å, range 0.5º-15º, step 0.002º, FWHM 0.01º. The structure solution tests were done by SA (simulated annealing) in DASH 3.2 software [3]. To speed up the computation of structures with more than 20 DOF we have used parallel processing obtained by MDASH extension. Influence of Mogul CSD based torsion angles bias on the calculation effectiveness was investigated as well. The results demonstrate the required number of SA steps depends exponentially on the problems DOF. This requires for problems close to 30 DOF about 10E+10 SA steps and years of single CPU computational time. The Mogul based bias can significantly help for compounds like peptides - e.g. for simulation based on compound CSD code AHAREH (4 peptides, DOF 24) the Mogul based calculation gives 50 times more often correct result than non-restricted SA run. We believe the 40 DOF structures can be solved routinely on 16-32 CPU clusters from perfect data not influenced by preferred orientation when the Mogul CSD torsion angels biased will be used (required total computational time about 1 month). Without developing a more efficient algorithm than SA solution we do not see a way how to get really close to the 300 DOF theoretical limits. The promising new algorithm can be a brute-force solution space sampling followed by local minimization as described in [4]. R&D of a code utilizing this idea is under progress.

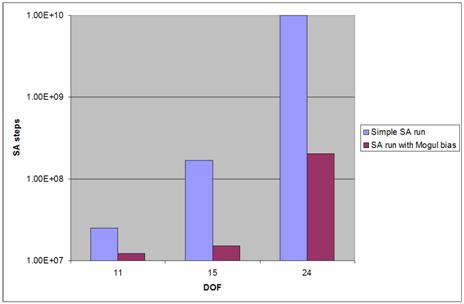
Fig 1.: Dependence of required simulated annealing steps number required to get one solution on DOF and the use of Mogul based bias.

1. David, W.I.F., Shankland, K. (2008). Acta Cryst A64, 52-64.

2. Fernandes, P., Shankland, K., Florence, A. J.,Shankland N., Johnston A. (2007) Journal of Pharmaceutical Science 96-5, 1192-1202

3. David, W.I.F., Shankland, K., Streek J., Pidcock, E., Motherwell S., Cole J. (2006). J. Appl. Cryst. 39, 910-915.

4. Shankland K., Markvardsen A.J., Rowlatt Ch., Shankland N., David W.I.F.: (2010). J. Appl. Cryst. 43,401-406

This work was supported by the Grant Agency of Czech Republic, Grant No. 106/14/03636S.