Twinning evolution as a function of loading direction in magnesium
J. Čapek, K. Máthis
1Department of Physics of Materials, Faculty of Mathematics and Physics, Charles University, Ke Karlovu 5, 121 16 Prague, Czech Republic
Keywords: magnesium, twinning, neutron diffraction
Introduction
Unique properties of magnesium alloys
predestine them for many applications. Especially transportation industry takes
advantage of their low density and high specific strength. Owing to their hexagonal
close packed (HCP) structure and c/a ratio close to ideal value the deformation
behavior differ from the other, e.g. fcc
of bcc metals. The lowest value of critical resolved shear stress (CRSS) is for
basal slip 
, followed by prismatic slip 
and first 
and second-order 
pyramidal slip system[1].
Combination of all systems having 
(i.e. 
) provides only 4 independent slip systems. Therefore, the von Mises
criterion requiring five independent slip systems for homogenous deformation is
not fulfilled and activation of second-order pyramidal system or mechanical
twinning is necessary. Since activation of second-order pyramidal system
requires high stresses or high temperatures, mechanical twinning is the
preferred deformation mechanism at room temperature.
In magnesium, the most easily activated
twinning mode is 
extension twinning. The
twinning on 
plane causes reorientation of
the lattice by 86.3° and extension along the c-axis of the twinned grain. Owing
to its polar nature different grains undergo twinning during tensile and
compressive deformation and different deformation texture evolution is
observed.
In the present paper the twinning evolution is studied using in-situ neutron diffraction technique. The main advantage of this method is in its capability to examine large sample volume owing to the deep penetration length of thermal neutrons. Furthermore, the intensity changes of particular diffraction peaks characterize the twinning and shift of diffraction peaks provides information about lattice deformation and internal stresses. The overall twinned volume can be determined from the intensity variations of particular peaks, caused by the crystal lattice reorientation during the twinning [2-5].
Experimental
technique
Cast polycrystalline magnesium with 1 wt.% Zr content was used for the
experiment. Zirconium additive stabilize the grain size to the value of 110 μm. The ND measurement showed that the initial samples
have random grain orientation distribution. (Fig. 1) The monotonic compression
and tensile tests was applied at room temperature at a strain rate of 
. The test was stopped for approx. 70 min at particular strain
values in order to collect the neutron diffraction data. The SMARTS engineering
instrument at LANSCE [6] was used for collecting the diffraction pattern. The
diffraction patterns were measured using two detector banks at ±90° to incident
beam. The angle between the incident beam and the loading direction was 45° [7].
This setup provides diffraction measurement of crystallographic planes both perpendicular
and parallel to the loading direction.
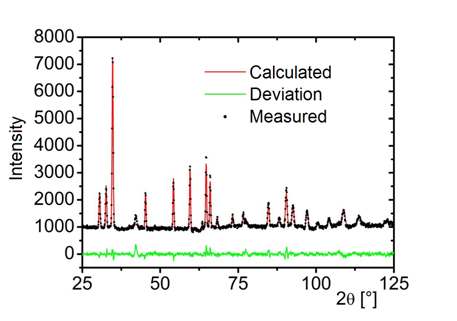
Figure 1. Measured ND pattern of initial state
compared with ideally random distribution.
The {00.2}–{10.0} parent-daughter system characterize well the twinning activity [8] owing to
the following reason: in tension those grains are ideally oriented for
twinning, which normal of the basal plane is parallel with the loading
direction. In the initial state those grains contribute to the 
peak. As extension twinning
occurs, part of the grains reorients by almost 90° and consequently increase of the 
peak can be observed. Since
in compression the grains having their c-axis perpendicular to the loading axis
are optimally oriented for extension twinning, the intensity changes have
opposite sense (Fig. 2).
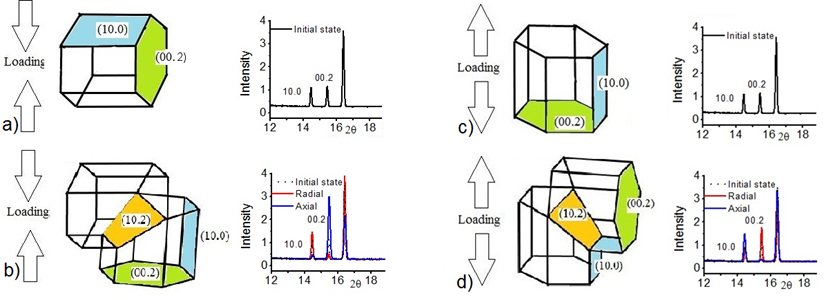
Figure 2. Comparison of ND pattern of initial state
(a,c) and after compression
(b) and tension (d)
Results
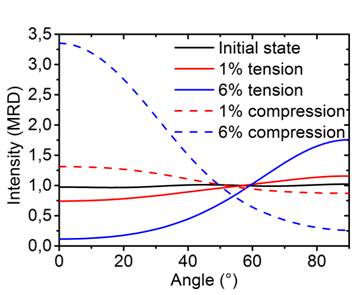
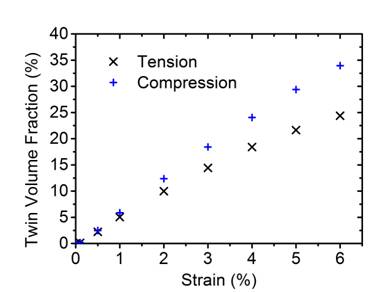
As demonstrated in [7], the determination of the twin volume fraction during the deformation is possible from the diffraction data by performing a 2-bank Rietveld refinement assuming an axisymmetric texture. The initial texture is random in the present case, and the uniaxial deformation is an axisymmetric operation, and hence the assumption should be valid. The refinements were done using the GSAS [9] and SMARTSware [10] software packages developed at Los Alamos National Laboratory. The axial distribution function was calculated for the 00.2 peak during deformation. The 0002 distribution is almost random at the start. When external stress is applied, the distribution of 0002 plane starts to change due to the twinning (Fig. 3). From the changes in the area under the curve above (tension) and below (compression) the cross-over point we can directly determine the twin volume fraction as described in [7]. Fig. 4 shows the twin volume fraction as a function of the absolute value of the applied strain for the tension and compression samples. In the entire range the twin volume fraction is larger for compression than it is for tension.
