XAFS study of Mn-doped Bi₂Se₃ and Bi₂Te₃ topological insulators

J. Růžička¹, O. Caha¹, V. Holý², G. Springholz³, H. Steiner³ and G. Bauer³

¹Department of Condensed Matter Physics and CEITEC, Masaryk University, Kotlářská 2, 611 37 Brno, Czech Republic

²Department of Electronic Structures, Charles University, Praha, Czech Republic

³Institut für Halbleiter- und Festkörperphysik, Johannes Kepler Universität, Altenbergerstrasse 69, 4040 Linz, Austria

ruzmen@physics.muni.cz

Keywords: topological insulators, magnetic doping, dopant position determination

Abstract

We study incorporation of Mn atoms into the lattice of topological insulators Bi₂Se₃ and Bi₂Te₃ grown by MBE on BaF₂ substrate. X-ray absorption fine structure around Mn K edge was measured and first coordination shell fits were made in order to investigate the nearest neighbours of Mn atoms. While in Bi₂Te₃ Mn atoms occupy distorted octahedral positions between Te layers, in the case of Bi₂Se₃ none of expected positions resulted in a good fit.

Introduction

Topological insulators attracted a lot of attention in recent years. While in the bulk they behave like ordinary insulators, their surface states are quite extraordinary. The 2D topological surface states have a conical energy-momentum dispersion and spins of electrons are locked to their momentum. Also due to time reversal symmetry the spins are protected from flipping. Such properties promise many applications in spintronics and quantum computing. Doping topological insulators by magnetic ions opens a gap in the energetic structure and allows for long-range magnetic order, thus further increasing possibilities of application. [1]

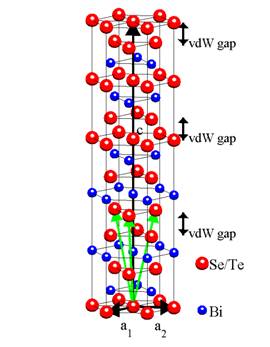
Among the most studied topological insulators are Bi₂Se₃ and Bi₂Te₃. Both materials have hexagonal structure of R3m symmetry. The unit cell consists of 15 atomic layers grouped in three quintuplets with Se/Te–Bi–Se/Te–Bi–Se/Te order (see Fig. 1a). The quintuplets are van der Waals bonded to each other by a double layer of Se/Te atoms – so-called van der Waals gap. 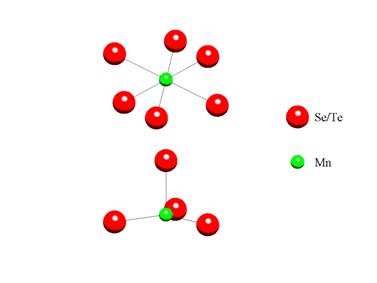[1] Because this gap is bigger than other interlayer distances in the structure, it is expected to host extrinsic atoms in the case of doping. There are two possible symmetric positions within the gap – distorted octahedral and distorted tetrahedral site, in both cases surrounded by Se/Te atoms (see Fig. 1b). Other possibility is that extrinsic atoms substitute Bi.

Experiment

The studied epitaxial layers of Bi₂Se₃ and Bi₂Te₃ were grown by MBE on cleaved BaF₂ substrates at substrate temperature 300–400 °C. The quality of the layers was monitored in-situ by RHEED.

The x-ray absorption fine structure (XAFS) spectra were obtained at beamline BM23 of ESRF, Grenoble at Mn K edge (6539 eV). Samples were measured with incident angle 2.5°. The detected signal was fluorescence radiation.

a)	b)

Figure 1. a) Hexagonal unit cell of Bi₂Se₃ and Bi₂Te₃ consisting of three quintuplets of atomic layers connected by van der Waals gaps. Basis vectors are in black, green arrows form an alternative rhombohedral basis. b) Possible positions of Mn atoms within the van der Waals gap – distorted octahedral (top) and distorted tetrahedral (bottom).

Results

Measured data were processed by Athena and fitting was performed using Artemis [2]. Theoretical spectra calculations were done by FEFF9 [3].

Bi₂Se₃

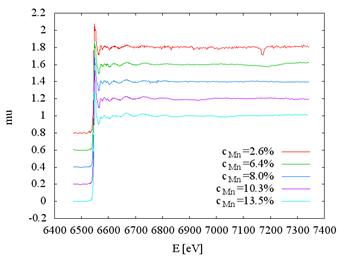
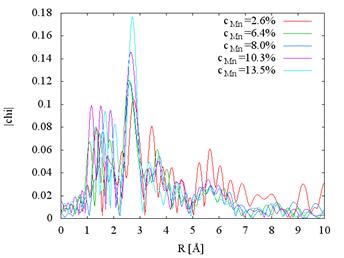
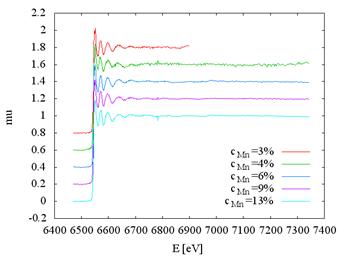
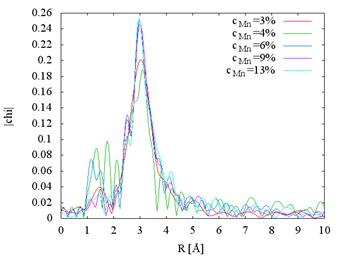
Measured data and the Fourier transforms for different Mn concentrations follow in Fig. 2.

a)	b)

Figure 2. a) Measured XAFS spectra of Mn-doped Bi₂Se₃ at Mn K edge, b) Fourier transforms.

Nearest neighbor distance can be estimated from the position of the first coordination shell peak of the Fourier transform; for Bi₂Se₃ they are summarized in Tab. 1.

Table 1. Nearest neighbour distances in Mn-doped Bi₂Se₃

nominal Mn concentration [%]	nearest neighbour distance estimate [Å]
2.6	2.76 ± 0.03
6.4	2.58 ± 0.03
8.0	2.61 ± 0.03
10.3	2.67 ± 0.03
13.5	2.70 ± 0.03

First calculations were made for three expected possible positions of Mn – octahedral and tetrahedral interstitial positions in the van der Waals gap and substitutional position at Bi site. Resulting spectra are compared with one of the measurements in Fig. 3. It is quite clear that none of the suggested positions matches the measurement. Trying to fit these models to the data produced no physically sound results.

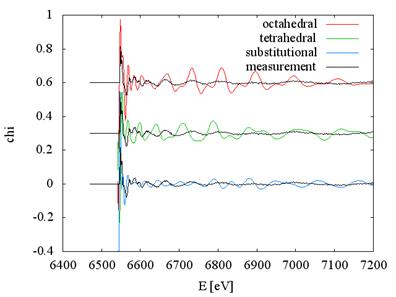
Figure 3. Comparison of measured and calculated spectra of Mn-doped Bi₂Se₃. Sample with Mn concentration 10.3%, calculation for three expected possible positions of Mn.

We have tried also combinations of the various Mn positions in the Bi₂Se₃ lattice, but to no success so far. A very characteristic feature of the measured spectra is the peak triplet near the edge, which we could not sufficiently reproduce.

Bi₂Te₃

Measured data and their Fourier transforms for different Mn concentrations follow in Fig. 4, nearest neighbour distances estimated from the first shell peak can be found in Tab. 2.

a)	b)

Figure 4. a) Measured XAFS spectra of Mn-doped Bi₂Te₃ at Mn K edge, b) Fourier transforms.

Table 2. Nearest neighbour distances in Mn-doped Bi₂Te₃

nominal Mn concentration [%]	n. n. distance estimate [Å]	n. n. distance from fit [Å]
3	3.04 ± 0.03	—
4	3.10 ± 0.03	—
6	2.98 ± 0.03	2.916 ± 0.008
9	3.01 ± 0.03	2.918 ± 0.008
13	2.98 ± 0.03	2.91 ± 0.01

We started again by calculating spectra of the three expected positions (see Fig. 5). In this case the octahedral position matches the measurement quite well. Data of the sample with lowest Mn concentration have a limited k-range because of artifact at about 6900 eV and the Fourier transform is therefore featureless and the fitting parameters have too large errors. 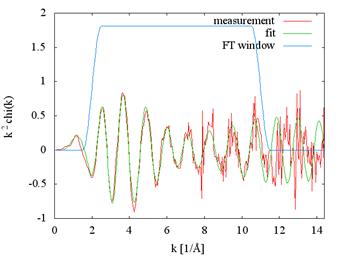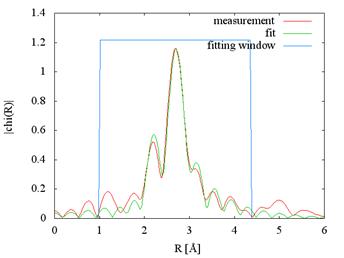Sample with 4% of Mn also couldn't be fitted, in this case due to many small glitches in the data. However the other three samples were fitted nicely, see for example Fig. 6. The model used contained the nearest six Te atoms and the two nearest Bi atoms. Resulting nearest neighbor distances are in Tab. 2.

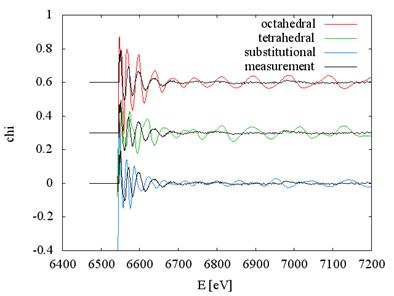
Figure 5. Comparison of measured and calculated spectra of Mn-doped Bi₂Te₃. Sample with Mn concentration 6%, calculation for three expected possible positions of Mn.

a)	b)

Figure 6. Best fit for sample with Mn concentration 9%. a) k-space, b) R-space.

Conclusion

We have successfully determined that in the case of Bi₂Te₃ Mn atoms are incorporated in octahedral positions within the van der Waals gap. In the case of Bi₂Se₃ none of the expected positions corresponds to the data and none of our attempts with combinations of the positions was successful. We hope further work will lead to successful determination also in this case.

References

[1] O. Caha, A. Dubroka, J. Humlíček, V. Holý, H. Steiner, M. Ul-Hassan, J. Sánchez-Barriga, O. Rader, T. N. Stanislavchuk, A. A. Sirenko, G. Bauer and G. Springholz, accepted to Crystal Growth & Design, DOI 10.1021/cg400048g.

[2] B. Ravel and M. Newville, Journal of Synchrotron Radiation, 12, 2005, p. 537.

[3] J. J. Rehr, J. J. Kas, M. P. Prange, A. P. Sorini, Y. Takimoto, F. D. Vila, Comptes Rendu Physique, 10, 2009, p. 548.

Acknowledgements.

The work was supported by the CSF project P204/12/0595. We thank Cornelius Strohm for assistance at beamline BM23 of ESRF synchrotron. ESRF participation is supported by INGO LA10010 project.