Structure, microstructure and residual stresses in borided steels

Z. Pala¹, R. Mušálek², J. Kyncl³, P. Harcuba⁴, J. Stráský⁴ , K. Kolařík¹

¹Department of Solid State Engineering, Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Trojanova 13, Prague, Czech Republic

²Department of Materials Engineering, Institute of Plasma Physics, Za Slovankou 1782/3, Prague, Czech Republic

³Department of machining, process planning and metrology, Faculty of Mechanical Engineering, Czech Technical University in Prague, Technická 4, Prague, Czech Republic

⁴Department of Physics of Materials, Faculty of Mathematics and Physics, Charles University in Prague, Ke Karlovu 5, Prague, Czech Republic

zdenek.pala@fjfi.cvut.cz

Keywords: boriding, surface hardening, iron borides, tooth-shaped microstructure, residual stresses.

Boriding or boronizing belongs to thermo-chemical diffusion-based surface hardening of iron materials. Even though it is comparatively rarely applied in industrial processes in comparison with other treatments, it can lead to substantial increase of service life, especially when extreme wear occurs on the surface. The main virtues of borided surface are not only the high hardness surpassing in some cases even 2000 HVN (Vickers hardness number), but also very low friction coefficient and above-average resistance to an array of acids and to high-temperature oxidation in a broad range of temperatures from ambient up to approximately 1000 °C. For example, the intrinsic hardness of Fe₂B is 1700 HVN or by order of magnitude higher than of pure iron with 130 HVN [1]. In general, whereas boriding leads to 1500 to 2000 HVN, the most widely applied treatments of nitriding and carburizing lead to 600 ÷ 1100 HVN and 700 ÷ 850 HVN, respectively [2]. At the same time, borided layers exhibit high thermal and electrical conductivity which can be an asset when compared with e.g. ceramic wear protective layers. Probably the main advantage of the borided process is such that it imposes virtually no limitations of the shape of the borided object, since the boron sublimates at higher temperatures from the boron source (typically powder) adjacent to the borided surface and penetrates into it via diffusion mechanism.

Both the boriding process and the structure of the resulting zone consisting of borided layers, base material and the interface in between them are intriguing since the complete description of the boriding mechanism is still lacking. Moreover, the structural phenomena involved encompass not only two distinct crystalline phases of tetragonal Fe₂B, which has three polymorphs with space groups I-4/mcm or I-42m, and orthorhombic FeB (Pbnm), but also substantial residual stresses differing both in values and even character in both phases and with appreciable stress gradient, texture is often present and also grain boundaries represent a fairly complex structural issue. From the microstructural point of view, the interface between the borided layers and base material is commonly described as having “tooth-shaped” or “saw-tooth” character as seen in Fig. 1. The spatial layout of the phases is usually such that FeB is on the surface and the needles in deeper layers are grains of Fe₂B. Consequently Fe₂B layers tend to exhibit higher degree of preferred orientation, most commonly fibre texture [3], yet texture of FeB layers is no exception. Since FeB is the brittler phase, the single phase borided layer of Fe₂B with good toughness is usually preferred to the duplex phase Fe₂B + FeB layer . Moreover, since the FeB is distinguished by almost triple value of thermal expansion coefficient when compared with the base material, it usually decomposes from the borided object during cooling after the boriding process, which is described as thermo-mechanical spalling.

In general, there are two parameters of borided surface which are being optimized via the boriding process conditions. Firstly, the effort is aimed at obtaining such microstructural morphology that would lead to better toughness and ductility coupled with sufficient adhesion of the borided layers facilitated by the tooth-shaped interface. Secondly, the spatial distribution of macroscopic residual stresses in the borided layers and the adjacent area of substrate should be such that would favour good cohesion within the hard layers and also contribute to the adhesion of the surface to the bulk.

Figure 1. “Tooth-shaped” microstructure of borided layers created in the surface of hard-to-work chromium ledeburitic steel X210Cr12 after 5 hours (left) and 12 hours (right) of boriding at 930 °C in powder.

The existence of texture significantly hinders the calculation of residual stresses in iron borides, especially in Fe₂B. So far, the texture was omitted in the calculation of residual stresses and we are currently developing an algorithm to take the effect of texture into account. In order to do this, single crystal elastic constants have to be known. There have been several attempts to calculate them using DFT (Density functional theory), but the results differ by as much as 100 %. Hence, residual stresses are calculated with macroscopic, or bulk, elastic constants in the generalized Hooke equation which can bring about unreliable results.

The aim of the hitherto carried out analyses was to ascertain whether boriding can bring beneficial effects to highly alloyed hard-to-work chromium ledeburitic steel X210Cr12 suitable for cold forming tools. The high levels of carbon (1.9 ÷ 2.2 wt%), silicon (0.1 ÷ 0.6 wt%) and especially chromium (11 ÷ 13 wt%) have so far rendered the boriding infeasible. This material is a standard for silica and alumina pressing tools or moulds which also explains the practical necessity to improve its wear resistance. Pursuing this aim, the real parts of pressing mould were borided for 5 and 12 hours, respectively. The resulting objects with borided surfaces were examined by SEM (Scanning electron microscopy), phase composition and residual stresses were determined from X-ray diffraction and microhardness was measured on the cross-section of the samples by Vickers indentor.

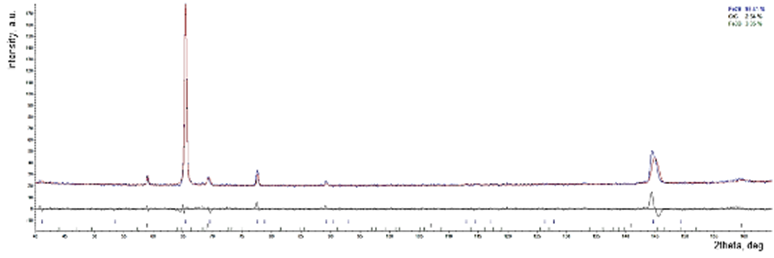
Figure 2. Result of Rietveld refinement showing dominant presence of Fe₂B, in order to take texture into account, March-Dollase metod was employed. The macroscopic residual stresses were not considered, hence the shift of modelled date at higher 2θ at 145°.

Micrographs from SEM revealed than the prolongation of processing time had only marginal effect on the borided layer thickness, increasing from approximately 30 to 40 μm. However, the important difference between both microstructures (see Fig. 1) is the change from duplex to almost single phase. This was verified by X-ray diffraction (CrKα radiation) when the diffraction patterns were obtained on the original free-surfaces and in depths of 10 and 20 μm. Phase identification revealed presence of both Fe₂B and FeB on the surface of 5h borided sample, but only FeB on 12h borided one. Both surfaces included also phases of iron borate Fe₃BO₅. After electro-chemical removal of 20μm thick surface layer, only Fe₂B was found in both samples; the 12h sample included also minor phase of CrC and Fe₃B while the 5h sample contained CrC, Cr₇C₃ and Fe₂₃(C,B)₆. Rietveld refinement of the 12h sample showed about 93 wt.% of Fe₂B as seen in Fig. 2, the comparatively bad match between the measured and modelled data at 145 °2θ is clear evidence of macroscopic residual stress presence which were not considered in this refinement. The most pronounced diffraction peak in Fig. 2 is from CrKα diffraction on textured (002) planes of Fe₂B and were the irradiated volume without preferred orientation this peak would have 25% relative intensity of (211) peak at approximately 70 °2theta.

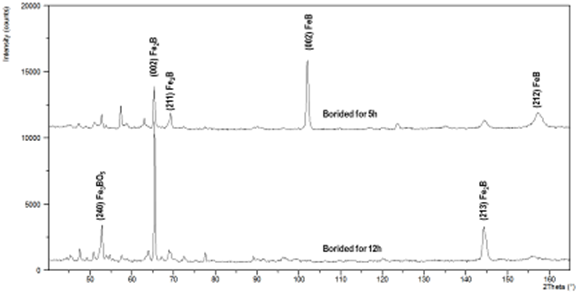
Figure 3. Comparison of diffraction patterns obtained on the surfaces of both samples.

Mutual comparison of diffraction patterns obtained at the surface of both samples is in Fig. 3. Measured values of microhardness in the borided layers were surprisingly small, i.e. 1350 ± 180 HVN and 1520 ± 220 HVN for 5h and 12h samples, respectively. The correct calculation of residual stresses was possible only for FeB, where (212) planes were measured in various orientations to the surface taking advantage of the so-called omega geometry. The resulting dependence of inteplanar lattice spacing versus sin²ψ was linear and the calculated value of macroscopic residual stress was approximately -300 MPa as seen in Fig. 4.

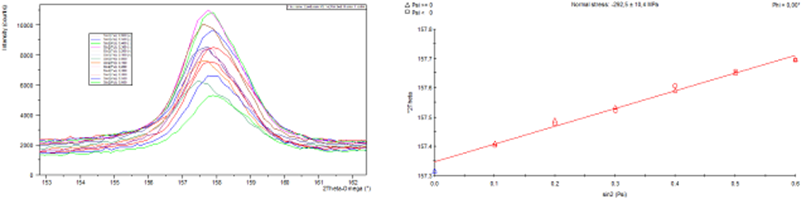
Figure 4. Measured diffraction profile of (212) planes of FeB (left) and 2θ vs. sin²ψ dependence from which the value of macroscopic residual stress was calculated.

References

1. C.T.Zhou, J.D. Xing, B.Xiao, Comp. Mat. Sci., 44, (2009), 1056-1064.

2. P. Gopalakrishnan, P. Shankar, M. Palaniappa, Met. and Mat. Trans. A, 33, (2002), 1475-1485.

3. R. Prűmmer, W. Pfeiffer, J. Less-Common Met., 117, (1986), 411-414.

Acknowledgements.

This research was carried out in the frame of research projects TA02011004 (Technology Agency of the Czech Republic).