Grazing incidence X-ray diffraction: study of depth distribution of chemical phase concentration
E. Dobročka1, P. Novák2, M. Vallo1, T. Lalinský1
1Institute of Electrical Engineering, Slovak Academy of Sciences, Dúbravská cesta 9, 841 04 Bratislava, Slovakia
2Institute of Nuclear and Physical Engineering, Faculty of Electrical Engineering and Information Technology, Slovak University of Technology, Ilkovičova 3, 812 19 Bratislava, Slovakia
edmund.dobrocka@savba.sk
Grazing incidence geometry is especially useful in X-ray diffraction analysis of thin films. The penetration depth of radiation can be easily changed by an appropriate selection of the angle of incidence α that enables obtaining information from different depths of the sample. Approaching the critical angle αc for total external reflection this depth can be decreased even to a nanometer scale. The method therefore provides an efficient tool for the analysis of depth distribution of various structural properties, such as the crystallite size, the amorphous fraction, stress or the concentration of chemical phase. While for most of these properties the absorption of the radiation can be characterized by an average attenuation coefficient μ, special care has to be paid to the last property. Variation of chemical phase concentration with depth usually results in depth dependence of the density and hence the attenuation coefficient. In the presented contribution a method for determination of depth distribution of a chemical phase is outlined. The method correctly takes into account the depth variation of the attenuation coefficient. The proposed method is verified on thin oxidized iridium layers. Three simple model cases are discussed and compared with the experimental results.
In the vicinity of critical angle the intensity of X-rays penetrating the homogeneous sample is exponentially damped according to relations [1]
(1)
(2)
where 
is the intensity of the incident beam, x is the depth coordinate, 
is the magnitude of the wave vector, δ and β are related to refractive index 
and depend on the electron density 
and the attenuation coefficient μ. When the composition of the layer
changes with depth, the parameters , μ, δ, β, and
B become a function of x and the intensity at the depth x is given as
(3)
In the simplest
case the layer contains only two crystalline phases with the weight fractions 
and 
, they are not necessarily
complementary, i.e. 
. If the thickness T of the analyzed layer is in the range
of nanometers, one can neglect the absorption of the
intensity of the diffracted beam and the total amount 
of the j–th phase (j = 1, 2) detected by measuring at the angle 
is proportional to the integral
(4)
The intensity of the incident
beam is included in the scaling factor SC. It should be pointed out that the
weight fractions 
appear also in B(x) through the weighted
values of the parameters δ(x) and β(x) according to
the composition of the layer at the depth x.
The total weight
fractions 
and 
of both phases are
given simply as
, 
(5)
The values
and 
can be directly compared with the results
obtained experimentally by measurement at various angles α and the profiles and can be determined by numerical procedure based
on an appropriate model.
In order to verify the capability of the
outlined approach very thin iridium layers deposited on sapphire/GaN/AlGaN system and subsequently annealed in oxidizing
atmosphere at 500 °C were analyzed by X-ray diffraction. The thickness of
the samples was determined by X-ray reflectivity measurement [2]. All
measurements were performed in parallel beam geometry with parabolic Goebel
mirror in the primary beam. The X-ray diffraction patterns were recorded in
grazing incidence set-up with the angle of incidence α = 0.3°, 0.4°, 0.5°,
0.6° and 1.5°. Two crystalline phases – Ir (PDF No.
03-65-1686) and IrO2 (PDF No. 00-15-0870) were identified.
Quantitative analysis of the measurements was performed by software TOPAS 3.0.
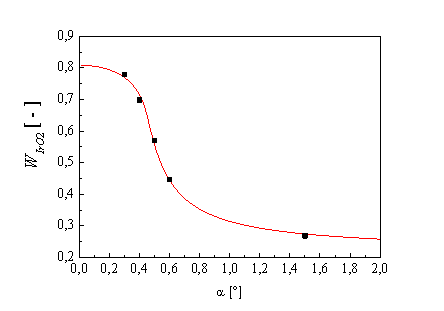
The results are shown in the Figure 2 (black squares).
The experimental results were analyzed within
the framework of three model structures of the oxidized Ir layer [3]. In the first model
the weight fraction of 
decreases gradually from the highest value 
at the surface. The depth profile of 
corresponds to complementary error function 
according to the expected oxygen diffusion
from the surface. The weight fraction of iridium is 
. The model has one free parameter –
the diffusion length 
. The second model consists of two sublayers 
(bottom) and (top) separated by an abrupt interface. The
free parameter is the depth 
of the interface. In the third model the 
and layers are separated by an amorphous interlayer. The model has two free parameters
– the depths 
and 
of the two interfaces.
The effect of the
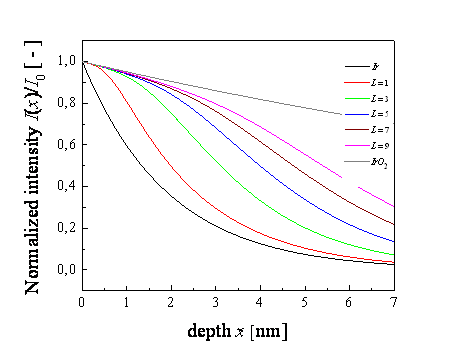
depth distribution of the phases on the intensity damping is shown in Figure 1.
The curves are calculated for the mixture of and according to the first model. Detailed
analysis [3] showed that the first and the second model are not able to explain
the large difference between the values of
– 0.78 and 0.27 measured at α = 0.3° and
1.5°, respectively. The third model was therefore accepted as the most appropriate.
The parameters and were optimized by least square method. The
best fit was achieved for the values 
and 
. The resulting
dependence 
is shown in Figure 2 (red curve).
|
|
|
|
Figure 1.
Normalized intensity as a function of depth x calculated for various diffusion lengths L (in nm). The black
and grey curves correspond to pure Ir and IrO2,
resp. The angle of incidence |
Figure 2.
Experimental (black squares) and calculated values (red curve) of the total
weight fraction |
References
1. M. Birkholz: Thin film analysis by X-ray scattering. Weinheim: Wiley-vch. 2006.
2. M. Vallo, T. Lalinský, E. Dobročka, G. Vanko, A. Vincze, I. Rýger, Appl. Surf. Sci., 267, (2013), 159.
3. P. Novák, Určenie hĺbkového profilu fázového zloženia tenkých vrstiev pomocou rtg difrakcie pri malom uhle dopadu, Diploma thesis, FEI STU, Bratislava, (2012).