Výpočetní postupy v molekulární dynamice

M. Pospíšil, M. Veteška

Univerzita Karlova v Praze, Ke Karlovu 3, 12116 Praha 2

pospisil@karlov.mff.cuni.cz

Keywords: molecular dynamics, statistical ensemble, thermostat, pressure control

Abstract

The general procedures used in molecular dynamics are described. Conditions of calculations under constant temperature and constant pressure in different statistical ensembles for various thermodynamics quantities are presented. Methods of molecular dynamics for the global minimum search are mentioned.

Molekulární dynamika

Molekulární dynamika [1-3] je založena na změnách poloh atomů v závislosti na silách, které na ně působí – jedná se o výpočet klasické pohybové rovnice. Síly se vypočítají z potenciální energie určené na základě parametrů silového pole. Molekulární dynamika je vhodná ke studiu časového vývoje systémů za nenulové teploty. Hlavní aplikace molekulární dynamiky jsou:

- Hledání konformací – během simulace se mění uspořádání systému, a tak lze zkoumat různé části stavového prostoru, které jsou pro model dostupné.

- Generování statistických souborů – použitím technik na kontrolování teploty a tlaku lze generovat statistické soubory, z nichž lze vypočítat různé energetické, termodynamické, strukturní a dynamické vlastnosti.

- Studium pohybu molekul – např. uzpůsobení se molekul do specifických tvarů, chemické reakce nebo odvození difúzních koeficientů.

Integrační algoritmus

Newtonova pohybová rovnice pro atom i se souřadnicemi ri je

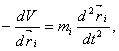(1)

kde V je potenciální energie. Tato rovnice je deterministická, tj. pro zadané úvodní souřadnice a rychlosti se dají pozice atomů určit v kterémkoli čase. Tyto určené souřadnice a rychlosti pro celou počítanou dynamiku se nazývají trajektorie. Rovnice se řeší metodou konečných diferencí, kdy ze známých souřadnic a rychlostí v čase t jsou spočteny souřadnice a rychlosti v čase t + Dt. Pro molekulární dynamiku je vhodný algoritmus, který je rychlý (potřebuje na jeden krok ideálně jen jedno vyhodnocení energie, protože to je pro velké modely časově velmi náročné), potřebuje málo paměti, umožňuje použít dlouhý časový krok Dt a dobře zachovává energii (zejména aby bylo možno generovat korektní statistické soubory).

Taková kriteria nejlépe splňuje Verlet-leapfrog algoritmus. Odvodí se pomocí rozepsání pohybové rovnice (1) s vhodným vyjádřením argumentů:

(2)

(3)

Tyto rovnice se přepíší jako numerické symetrické derivace

(4)

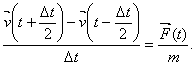(5)

Vlastní algoritmus začíná nastavením v čase t poloh r(t) a v čase t − Dt/2 rychlostí v(t − Dt/2) Poté se provádí kroky:

1. Výpočet síly v čase t

(6)

2. Přepočtení rychlostí v čase t + Dt/2

(7)

3. Přepočtení poloh v čase t + Dt

(8)

4. Posunutí času t = t + Dt a pokračování prvním krokem.

Výhodou tohoto algoritmu je právě jeden výpočet síly na jeden časový krok, malá spotřeba paměti a relativně dlouhé časové kroky. Nevýhoda je, že polohy a rychlosti jsou vypočteny v polovičním kroku od sebe. Tento problém nemá Verletův rychlostní algoritmus, ten ovšem potřebuje navíc paměť pro uložení vypočtených sil z předešlého kroku. V případě potřeby přesnější trajektorie se větší chyby Verletovy metody dají kompenzovat průměrováním přes sadu trajektorií. Jiné, přesnější algoritmy, např.Rungeho–Kuttaova metoda se obvykle nepoužívají, neboť vyžadují v každém kroku několikanásobný výpočet sil. Podrobnosti o uvedených algoritmech lze nalézt např. v [4 – 6].

Časový krok se volí co nejdelší, ovšem příliš dlouhé kroky zapříčiňují nestabilitu a nepřesnost výpočtu. V případě molekulárních simulací je třeba zvážit také omezení modelu, které je dáno zejména pohybem atomů s nejvyššími frekvencemi (vodík), a zvolit takový krok, aby byl splněn předpoklad, že během jednoho kroku jsou rychlosti a zrychlení konstantní.

Statistické soubory

Výpočet pohybových rovnic prochází plochu konstantní energie systému. Nicméně v přirozeném případě je systém většinou vystaven vnějšímu tlaku nebo vyměňuje teplo s okolím a celková energie se nezachovává. Existují metody, jak rozšířit molekulární dynamiku, aby se dala teplota a tlak kontrolovat. V závislosti na tom, které stavové veličiny se zachovávají konstantní, se dají generovat různé statistické soubory.

NVE soubor

Jedná se o tzv. mikrokanonický soubor, je adiabatický (tzn. k výměně tepla nedochází), konstantní je celková energie a objem. Získá se standardním řešením Newtonových rovnic. K fluktuacím energie dochází jen díky zaokrouhlovacím chybám, tedy tento soubor je vhodný, když je třeba prozkoumat povrch konstantní energie nebo když je potřeba se vyhnout fluktuacím vznikajícím kontrolou teploty a tlaku. Teplota fluktuuje okolo průměrné hodnoty v závislosti na tom, jak se přeměňuje energie mezi kinetickou a potenciální energií.

NVT soubor

Jde o tzv. kanonický soubor, je izotermický, tzn. dochází k výměně tepla s termostatem, konstantní je termodynamická teplota a objem. Používá se buď pro systémy, u nichž tlak není potřebný faktor, aby se jeho ignorováním zmenšily fluktuace trajektorie, nebo pro systémy bez periodických okrajových podmínek, protože u těchto systémů tlak nelze definovat.

NPT soubor

Konstantní je teplota i tlak. Použitelný je jen pro periodické systémy, neboť kontrola tlaku se provádí změnami velikosti mřížové buňky. Je vhodný např. k nastavení rovnováhy s požadovanou teplotou a tlakem před následnou simulací v NVE souboru.

Kontrola teploty

Termodynamická teplota je makroskopická stavová veličina, která má smysl pouze pro systém v rovnováze. Teplota má k mikroskopickému popisu systému vztah přes kinetickou energii, tj. přes rychlosti atomů. Maxwellovo–Boltzmannovo rozdělení popisuje v rovnovážném systému o teplotě T pravděpodobnost f(v), že atom o hmotnosti m má velikost rychlosti v:

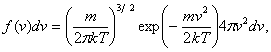(9)

kde k je Boltzmannova konstanta. Velikosti kartézských složek rychlosti v_x mají Gaussovo rozdělení pravděpodobnosti g(v_x)

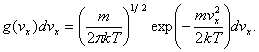(10)

Termodynamická teplota se měří z průměrné kinetické energie systému, s kterou souvisí přes ekvipartiční teorém, který říká, že každému stupni volnosti přináleží průměrná energie kT/2. Tzv. kinetická teplota T_kin a okamžitá kinetická energie K tak mají vztah

(11)

kde N_f je počet stupňů volnosti a N je počet atomů s rychlostmi v_i. Termodynamická teplota T je průměrem kinetické teploty T_kin, tedy platí

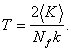(12)

Počet stupňů volnosti N_f bývá v neperiodických systémech 3N − 6, protože každý atom má 3 složky rychlosti, od čehož je 6 stupňů odečteno, neboť rotace a translace těžiště jsou ignorovány. V periodických systémech jich je obvykle 3N - 3, protože se ignorují jen translace těžiště.

Ačkoliv na začátku simulace se atomům přiřadí rychlosti podle Maxwellova–Boltzmannova rozdělení při dané teplotě, během simulace rozdělení nezůstává stejné. To se děje zejména tehdy, když simulace nezačíná ze struktury, která je zcela minimalizovaná. Rovněž se během simulace mění teplota, když se minimalizovaná struktura mění ve strukturu v teplotní rovnováze a kinetická energie přechází v potenciální energii.

Konstantní teplota se udržuje algoritmy, které musí upravovat rychlosti atomů tak, aby dohromady dávaly teplotu korektně, tedy podle Maxwellova–Boltzmannova rozdělení. K tomu je třeba navíc zaručit vytváření korektního statistického souboru, tj. že pravděpodobnost výskytu jisté konfigurace se chová podle statistických zákonů. Např. pro soubor NVT to znamená, že pravděpodobnost výskytu konfigurace s energií E je úměrná tzv. Boltzmannovu faktoru exp(−E/kT).

Přímé přeškálování rychlostí

Jde o drastický způsob změny rychlostí atomů tak, aby bylo přesně dosaženo žádané teploty. Ačkoli je to velmi efektivní způsob, během simulace se obyčejně nepoužívá, protože neprodukuje korektní statistický soubor, potlačuje přirozené fluktuace systému. Používá se k rychlé změně teploty během snahy dostat systém do rovnovážného stavu s požadovanou teplotou.

Berendsenův termostat

Tato metoda lze použít pro rovnovážný systém a dává již dobré přiblížení kanonickému souboru. Každá rychlost je znásobena faktorem

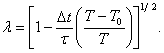(13)

kde Dt je délka kroku, τ je charakteristický relaxační čas, T₀ je požadovaná teplota a T je okamžitá kinetická teplota [7].

Noseho–Hooverův termostat

Tato metoda je složitější a je třeba použít Hamiltonián systému. Výsledkem je přesný kanonický soubor. V metodě se pro reprezentaci interakce s termostatem přidává k modelu fiktivní stupeň volnosti s vhodnou hmotností a korektním potenciálem. Výpočet pohybových rovnic s konstantní energií (tj. v NVE souboru) pro rozšířený systém pak vede k NVT souboru pro reálný model [8-11].

Andersenova metoda

Tato metoda je založena na tom, jakým způsobem je ovlivňována teplota v reálném systému. Jedna verze Andersenovy metody změní v každém kroku rychlost jednoho atomu podle Boltzmannova rozdělení. Jiná verze náhodně mění s předem danou kolizní frekvencí rychlosti všech atomů.

Kontrola tlaku

Tlak je termodynamická stavová veličina. Počítá se využitím viriálového teorému [12]. Okamžitý tlak P při kinetické teplotě T, objemu systému V , v němž je N částic, je

(14)

W je vnitřní viriál

(15)

kde r_i jsou pozice atomů a f_i jsou síly na ně působící. Termodynamický tlak je průměrem okamžitého tlaku.

Tlak může být definován jen v případě, kdy je systém v nějaké buňce o daném objemu. V případě molekulových simulací je to mřížová buňka, proto lze tlak spočíst jen pro periodické modely. Stejně jako v případě teploty musí metody na kontrolu tlaku vytvářet korektní statistické soubory. Metody jsou podobné jako u teploty.

Berendsenova metoda

V této metodě je tlak upravován změnou souřadnic částic a velikosti buňky, a to tak, že v každém kroku jsou jak všechny tři souřadnice každého atomu, tak vektory mříže znásobeny stejným faktorem

(16)

v němž Dt je krok, P je okamžitý tlak, P₀ je žádaný tlak a γ a τ jsou volitelné parametry stlačitelnost a relaxační čas. U této metody se projevují výrazné fluktuace a není ji vhodné obecně používat [13].

Andersenova metoda

V této metodě je objem brán jako proměnná systému. K Lagrangiánu systému jsou přidány dva členy: člen reprezentující kinetickou energii mříže, který má jako parametr volitelně definovanou hmotnost, a člen reprezentující elastickou energii, jež je součin PV tlaku P a objemu buňky V. Z tohoto Lagrangiánu se odvozují pohybové rovnice pro atomy a mřížové vektory [14].

Pokud je třeba simulovat za neizotropního tlaku, používá se Parrinellova–Rahmanova metoda [15], která je obdobná Andersenově metodě.

Obecný postup dynamických výpočtů

Dynamické simulace probíhají ve dvou fázích: dosažení rovnovážného stavu s požadovanými podmínkami a vlastní simulace (sbírání dat, produkční fáze). Každá z nich představuje samostatnou dynamickou simulaci.

Za rovnovážný stav se považuje konfigurace systému, která nejvíc odpovídá požadované teplotě a tlaku. Jeden ze způsobů jak poznat, zdali bylo rovnováhy dosaženo, je měřit v závislosti na čase termodynamické veličiny, jako jsou energie, teplota, tlak. V rovnováze tyto veličiny fluktuují okolo svých průměrných hodnot, které jsou v čase konstantní. Ovšem zcela dostatečný test to není, neboť konfigurace se může náhle změnit i po dlouhé době. Jistější způsob ověření rovnováhy je začít výpočet z různých počátečních konformací s různými rychlostmi. Pokud dokonvergují k podobným konformacím a vlastnostem, bylo pravděpodobně rovnováhy dosaženo.

Na začátku fáze hledání rovnováhy se atomům přiřadí rychlosti podle Maxwellova–Boltzmannova rozdělení a během hledání rovnovážného stavu je možno teplotu udržovat i přímým přeškálováváním rychlostí. Pokud je systém velký, může trvat poměrně dlouho najít rovnovážný stav, protože je třeba prohledat rozsáhlý stavový prostor. Na dobu hledání rovnováhy má rovněž negativní vliv, pokud jsou velké energetické bariéry mezi lokálními minimy a globálním minimem.

Následná simulace po dosažení rovnováhy již slouží k zaznamenávání údajů o systému. Teplotu v této fázi nelze kontrolovat přímým přeškálováváním rychlostí. K dosažení rovnováhy je možno použít jiný statistický soubor než pro následnou produkční fázi a je samozřejmě možné z jednoho rovnovážného modelu pokračovat ve více simulacích za rozdílných podmínek.

Nalezení globálního minima

Lze předpokládat, že model s nejmenší celkovou energií bude pravděpodobně také ten nejrealističtější. Proto cílem molekulárního modelování je nalézt globální energetické minimum. To se provádí změnami všech stupňů volnosti, jimiž jsou pozice atomů, rozměry mříže atd. Zmíněné klasické minimalizační algoritmy (viz. P. Kovář: Výpočetní metody v molekulární mechanice) většinou dokáží najít jen lokální minima, která jsou blízko výchozí konformace, neboť tyto algoritmy ignorují konformace, jejichž energie je vyšší. Jedině procházením celého povrchu energie, který je dán zmíněnými stupni volnosti, lze nalézt globální minimum. Pro nalezení globálního minima je třeba mít metody pro generování velkého množství výchozích modelů s rozdílnými konformacemi. Tyto metody lze rozdělit podle přístupu do třech skupin:

1. deterministické systematické procházení celého povrchu energie,

2. stochastické metody (např. Monte Carlo, genetické algoritmy),

3. molekulární dynamika.

Pochopitelně nejspolehlivějšími metodami je procházení celého povrchu energie, tj. prostoru všech možných stavů např. krystalu. Toto je možné pouze pro malé modely, neboť pro velké struktury významně narůstá výpočetní čas, a je třeba použít další dva přístupy.

Nutno ještě dodat, že hledat globální minimum má smysl zejména u malých molekul (dosažení globálního minima lze poznat tak, že minimalizační algoritmy k němu dokonvergují z vícero rozdílných výchozích konformací). U větších struktur často existuje několik různých konformací, které jsou v lokálním minimu a mají obdobnou energii, a tudíž se mohou všechny vyskytovat. Metody na hledání globálního minima pak místo toho slouží k nalezení všech takto možných stavů.

Deterministické procházení stavového prostoru

Tyto metody spočívají ve vygenerování mnoha hrubých výchozích konfigurací, tzv. iniciálních modelů, z nichž ty nejvhodnější jsou následně minimalizovány. Aby bylo opravdu nalezeno globální minimum, iniciální modely musí pokrývat celý prostor možných stavů. U různých konformací molekuly se příliš neliší délky a úhly vazeb, ale torzní úhly. Proto konkrétní algoritmus výběru iniciálních modelů obyčejně spočívá v systematických změnách všech torzních úhlů molekuly.

Stochastické metody

Tyto metody nedokáží obecně prohledat celý stavový prostor, ale většinou se jedná o vytváření nových iniciálních modelů z již dříve minimalizovaných modelů s vložením náhodných malých změn. Tyto iniciální modely jsou pak zase standardně minimalizovány.

Nejčastějšími metodami jsou torzní Monte Carlo, kartézské stochastické metody nebo na genetických algoritmech založené metody, které využívají celé sady výchozích minimalizovaných modelů, jež jsou postupně vylepšovány jejich vzájemným ovlivňováním.

Typy molekulární dynamiky

Molekulární dynamika lze použít i za účelem vytváření nových konformací. Požadavek rovnovážnosti není třeba a na vhodné procházení prostoru stavů se používají jiné, odpovídající techniky dynamiky. Molekulární dynamika využívá kinetické energie atomů k překonání potenciálových bariér. To jí umožňuje dosáhnout stavů molekul, které jsou pro minimalizaci nedostupné. Délka dynamiky bývá nejvýše několik nanosekund, což je příliš málo na významnou změnu konformace. Proto se molekulární dynamika hodí k efektivnímu prozkoumání lokálního prostoru stavů, ale nelze ji v tomto případě užít k hledání globálního minima. Toto omezení se snaží překonat některé speciální techniky dynamiky, používající případně vyšší teploty (lze použít i klasickou dynamiku za vyšší teploty, která umožňuje překonat velké energetické bariéry). Lze využít např. následující typy dynamik:

„Quenched” dynamika (zhášená)

Tato technika nezvyšuje možnosti dynamiky nalézt globální minimum, ale prochází dosažitelný prostor stavů užitečněji. Je to kombinace klasické dynamiky a minimalizace. Pravidelně, po jistém počtu kroků dynamiky je struktura minimalizována. Poté dynamika pokračuje od stavu před minimalizací. Minimalizované stavy se zaznamenávají odděleně od stavů dosažených během dynamiky. Tuto metodu lze kombinovat s jinými technikami dynamiky.

Dynamika „simulated annealing“ (žíhací)

V této technice se teplota ve zvolených krocích zvyšuje z původní k cílové teplotě a poté zase zpět. Tento cyklus se případně několikrát opakuje. Zvýšení teploty umožní překonat i vysoké energetické bariéry.

Při kombinaci s Quenched dynamikou se minimalizuje stav s nejmenší energií během posledního cyklu.

Impulsní dynamika

Impulsní dynamika umožňuje před spuštěním výpočtu přiřadit výchozí rychlosti o určitém směru vybraným atomům. Takto lze rovněž překonat energetické bariéry.

References

1. P. Comba, T. W. Hambley, Molecular Modeling of Inorganic Compounds. VCH, Weinheim, 1995.

2. M. Veteška, Molekulární simulace ve strukturní analýze interkalátů. MFF UK Praha 2006.

3. Cerius² User Guide, Forcefield Based Simulations. Molecular Simulations Inc., San Diego, 2000.

4. W. H. Press, B. P. Flannery, S. A. Teukolsky, W. T. Vetterling, In Numerical Recipes, The Art of Scientific Computing. Cambridge University Press, Cambridge, 1986.

5. L. Verlet, Phys. Rev., 159, (1967), 98 – 103.

6. I. Nezbeda, J. Kolafa, M. Kotrla, Úvod do počítačových simulací metody Monte Carlo a molekulární dynamiky, Karolinum, Praha 1998.

7. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola, J. R. Haak, J. Chem. Phys., 81, (1984), 3684-3690.

8. S. Nosé, Molec. Phys., 52, (1984), 255-268.

9. S. Nosé, J. Chem. Phys., 81, (1984), 511-519.

10. S. Nosé, Prog. Theoret. Phys. Supplement, 103, (1991), 1-46.

11. W. Hoover, Phys. Rev. A, 31, (1985), 1695-1697.

12. M. P. Allen, D. J. Tildesley, Computer Simulation of Liquid, Claredon Press, Oxford Science Publications, 1987.

13. D. Brown, J. H. R. Clark, Molecular Physics, 51, (1984), 1243-1252.

14. H. C. Andersen, J. Chem. Phys., 72, (1980), 2384-2393.

15. M. Parrinello, A. Rahman, J. Appl. Phys., 52, (1981), 7182-7190.