Výpočetní postupy v molekulární mechanice

Výpočetní postupy v molekulární mechanice

P. Kovář, M. Veteška

Univerzita Karlova v Praze, Matematicko-Fyzikální fakulta, Ke Karlovu 3, 121 16 Praha 2

Kovar@karlov.mff.cuni.cz

Keywords: potential functions, molecular mechanics, minimization algorithms.

Abstract

The types of interatomic potential functions used in molecular simulations are described. Methods of calculations of non-bonded interactions are mathematically described and algorithms used in molecular mechanics are discussed.

1 Úvod

Vlastnosti systémů (krystaly, molekuly), jako jsou jejich stabilita, mechanické vlastnosti, hustota, infračervená a rentgenová spektra, atd., souvisejí s jejich strukturou. Je proto vhodné vytvořit algoritmy a programy, které jsou schopny vypočítat strukturu vyšetřovaných systémů, na základě jejíž znalosti budeme pak schopni odvodit požadované vlastnosti. Molekulární simulace jsou jednou z těchto technik, které nám umožní strukturu daného systému určit. Především kvůli jednoduchosti a efektivitě pro velké struktury patří k nejrozšířenějším. Při uvažovaných velikostech struktur řádově ve stovkách až tisících atomů na jednu krystalovou buňku je nemožné v současnosti vypočítat strukturu ab-initio výpočty. Princip molekulárních simulací spočívá ve výpočtu potenciální energie pro dané uspořádání atomů (popř. atomů krystalové buňky) pomocí empirických silových polí. V tomto zjednodušeném popisu je energie systému určena započtením všech sil mezi atomy, přičemž výpočet je založen na mechanickém přístupu, tj. atomy se chovají jako mechanické oscilátory. Molekulární simulace spočívají v určení celkové potenciální energie systému a její minimalizace, kde energie je dána pomocí empiricky určených funkcí a jejich parametrů. Tyto funkce a parametry se dohromady nazývají silové pole. V silovém poli jsou výrazy pro popis vazeb mezi atomy a výrazy pro nevazebné interakce, které závisí jen na vzdálenosti mezi atomy – jedná se o elektrostatické a van der Waalsovy interakce a vodíkové můstky. Ze všech členů se pak pro konkrétní model utvoří výraz pro energii, která je funkcí souřadnic atomů v daném modelu. Celková potenciální energie systému je tedy vyjádřena jako součet vazebních E_vaz a nevazebních E_nvaz interakcí [1, 2]:

E = E_vaz + E_nvaz(1)

1.1 Vazebné interakce

Vazební člen v sobě zahrnuje členy, které charakterizují kovalentní vazbu pomocí jednoduchých analytických funkcí. Platí:

E_vaz = E_b + E_θ + E_φ + E_δ . (2)

E_b (tzv. „bond stretch“ člen) popisuje deformaci vazebné délky. V harmonické aproximaci představuje pružnou část vazebné síly danou Hookovým zákonem:

(3)

kde k_ij je silová konstanta a r_ij⁰ je ideální vazebná délka. Případná anharmonicita potenciální energie se zohledňuje např. pomocí tzv. Morseho potenciálu:

(4)

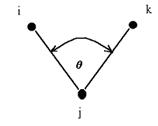
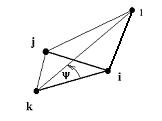
kde D₀ je vazební energie. E_θ popisuje deformaci vazebního úhlu mezi párem atomů i a k, které jsou navíc vázány k jednomu společnému atomu j (viz obr. 1):

(5)

kde k_ijk je síla pružiny udržující vazební úhel θ_ijk mezi atomy i, j, k na ideální hodnotě θ_ijk⁰ .

Obr. 1 Vazební úhel mezi třemi atomy.

Pro vazby s úhlem blízko π tento vztah příliš nevyhovuje, proto se do vztahu zavádí vyšší

mocniny 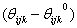, nebo se nahrazuje různými typy kosinového rozvoje, z nichž nejjednodušší má tvar

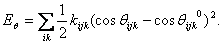(6)

Jako doplněk k E_θ slouží člen E_UB(tzv. Urey-Bradley potenciál), který je v nejjednodušším tvaru dán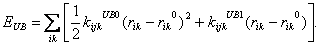

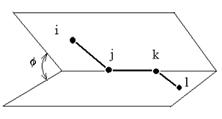
(7)

 je deformace úhlové torze, jež popisuje geometrii 4 atomů i, j, k, l a je charakterizována úhlem  mezi rovinami určenými polohami atomů ijk a jkl (viz obr. 2). Nejjednodušší tvar pro  je:

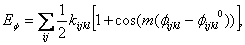(8)

kde k_ijkl je výška rotační bariéry okolo torzního úhlu 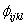, m je periodicita potenciálové funkce a  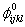je předpokládaná rovnovážná hodnota úhlu.

Obr. 2 Úhlová torze

E_δje tzv. inverzní člen, který popisuje vazební geometrii 4 atomů charakterizující odchylky od planárního uspořádání (proto také zvaný „out-of-plane deformace). Podle potřeby se používají tři různé popisy:

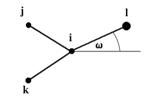
Umbrella inverze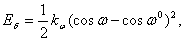

(9)

kde k_ω je silová konstanta, ω je úhel mezi osou il a rovinou ijk a ω⁰ je rovnovážná hodnota tohoto úhlu.

Obr. 3 Umbrella inverze

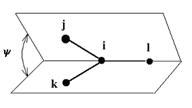
Amber inverze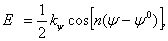

                                                                                                      (10)

kde k_ψ je energetická rotační bariéra, n periodicita, ψ je úhel mezi rovinami jil a kil                                                            (viz obr. 4) a ψ⁰ je rovnovážná hodnota tohoto úhlu. Pro planární uspořádání je n = 2 a            ψ⁰ = 180° a pro tetraedrickou koordinaci je n = 3 a ψ⁰ = 120° .

Obr. 4 Amber inverze

Charm inverze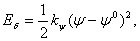

                                                                                                             (11)

kde k_ψ je silová konstanta, ψ je úhel mezi rovinami ijk a ljk a ψ⁰ je rovnovážná hodnota tohoto úhlu.

Obr. 5 Charm inverze

1.2 Nevazebné interakce

Nevazebné interakce E_nvaz zahrnují elektrostatické E_ela van der Waalsovy interakce E_vdW  a vodíkové vazby E_Hb .

Pro Coulombické interakce platí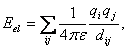

                                                                                                                (12)

kde q_i a q_j jsou náboje atomů i a j, d_ij jejich vzdálenost a ε dielektrická konstanta. Náboje jsou buď celočíselné (pro ionty), nebo parciální, reprezentující polaritu molekuly (dipól, kvadrupól, atd.). Van der Waalsovy interakce se počítají buď pomocí exponenciálního výrazu, tzv. Buckinghamova potenciálu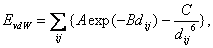

                                                                                           (13)

kde A, B, C jsou konstanty a d_ij vzdálenost atomů. Další výraz pro van der Waalsovy interakce je Lennardův-Jonesův potenciál: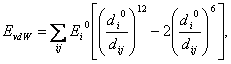

                                                                                      (14)

kde −E_i⁰ je minimální vdW energie atomu, d_i⁰/2 jeho tzv. van der Waalsův poloměr a d_ij vzdálenost atomů. Vodíkové vazby se počítají podobným způsobem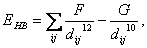

                                                                                                           (15)

kde F , G jsou konstanty a d_ij vzdálenost páru donor-akceptor.

Omezení dosahu interakcí

Složitost výpočtu nevazebných interakcí kvadraticky závisí na počtu atomů v systému, což pro větší systémy může představovat problém a je třeba učinit ořezání (cut-oﬀ), tj. stanovit mez, nad kterou se interakce mezi atomy zanedbávají nebo počítají přibližně. Zejména pak pro krystaly, kde sumace ve vztazích pro tyto interakce obsahuje nekonečný počet členů,

je nezbytné omezení a existují metody, jak tyto sumy počítat efektivním způsobem, např. Ewaldova sumace [3]. Je třeba rozlišit krátkodosahové interakce klesající rychleji než 1/d³ (např. Lennardův-Jonesův potenciál, která klesá jako 1/d⁶ ), které je možno zanedbat již pro vzdálenosti větší než několikanásobek interakčního minima, a dalekodosahové interakce (např. Coulombická interakce slábnoucí jako 1/d pro interakci náboj-náboj), které nelze již jednoduše pro větší vzdálenosti zanedbat. Je možno například provést přímé ořezání, kdy jsou interakce nad jistou vzdálenost ignorovány. Tato metoda ale může vést k nespojitostem v ploše energie a jejích derivacích. Tento problém se řeší přechodovými funkcemi, které vedou k hladkému přerušení interakcí. Větším problémem u této přímé metody je rozdělení dipólů, kdy jeden z pólů zůstane pod hranicí ořezu a druhý nad a vzniká tak nefyzikální monopól. Protože příspěvek k energii z interakce monopólů je o pár řádů větší než z interakce dipólů zformovaných z monopólů, takové rozdělení dipólu přináší velké chyby výpočtu energie a je třeba mu předejít. Řeší se to např. metodou ořezávání po nábojových skupinách, což jsou malé skupiny blízkých atomů, které mají společný náboj dostatečně blízko nule. Nábojovými skupinami bývají obvykle běžné chemické funkční skupiny. Pro periodické systémy jsou přesnější a efektivnější metody na výpočet nevazebných interakcí, než je metoda ořezávání. Jedná se o multiplovou metodu a především Ewaldovu sumaci.

Ewaldova technika je podrobně popsána v [3]. Spočívá v rozdělení mřížové sumy na dva členy. Mřížová suma je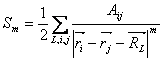

                                                                                                       (16)

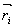kde a 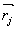 jsou bázové vektory atomů i a j a 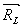je mřížový translační vektor, přičemž sumy

přes i a j jdou každá přes všechny atomy v buňce. První člen z mřížové sumy vznikne jejím

vynásobením konvergenční funkcí φ(r), která rychle klesá s r, druhý člen pak vynásobením             1 − φ(r):

                                              (17)

První člen velmi rychle konverguje. Druhý člen lze Fourierovou transformací převést na  rychle konvergující sumu v reciproké mříži. Obě sumy lze tedy omezit na jistý počet členů. Konvergenční funkce je pro elektrostatickou energii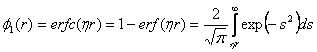

                                                                 (18)

a pro rozptylovou energii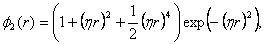

                                                                              (19)

kde parametr η slouží k vyrovnání rychlosti konvergence mezi sumami v reálném a reciprokém prostoru. Doba výpočtu sum závisí na zvolené velikosti omezení, tj. kolik členů z nekonečných sum se skutečně započte.

1.3 Výpočet nábojů

Náboje mohou být pro jednotlivé atomy přiřazeny tzv. tabulkovou metodou, kdy příslušný parciální náboj pro daný atom v systému je odvozen například na základě kvantově-mechanických výpočtů, případně na základě experimentálních dat. K výpočtu rozložení nábojů v molekule se používá metoda Charge equilibration (QEq), která rozložení nábojů spočte v závislosti na geometrii molekuly. Metoda vychází z vyjádření energie izolovaného atomu A jako funkce jeho náboje Q_A. Rozvoj této energie E_A(Q_A ) do Taylorovy řady má tvar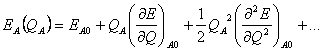

                                                               (20)

Pro atomy s nábojem +1 a -1 platí: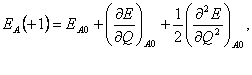

                                                                                 (21)

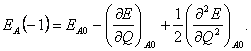                                                                                 (22)

Odečtením a sečtením předchozích rovnic dostaneme: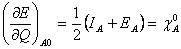

                                                                                                   (23)

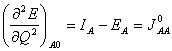                                                                                                     (24)

kde 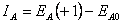 je ionizační energie (energie potřebná k odtržení elektronu z neutrálního atomu), 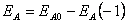je elektronová aﬁnita (energie uvolněná při vzniku aniontu z neutrálního atomu) a χ_A⁰ je elektronegativita atomu (schopnost daného atomu  přitahovat elektrony). Pro pochopení fyzikálního smyslu (24) lze uvažovat atom s orbitalem  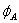obsazeným jen jedním elektronem. Při odtržení elektronu je orbital atomu prázdný, při

zachycení elektronu je orbital obsazený dvěma elektrony. 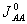, dané rozdílem I_A a E_A, je tak Coulombická repulze mezi dvěma elektrony na orbitalu 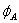. Vztah pro energii izolovaného atomu (20) lze přepsat s použitím (23) a (24) na

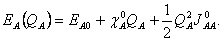                                                                                        (25)

Celková energie systému se získá vysčítáním přes všechny atomy: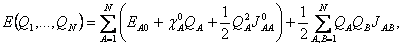

                                           (26)

kde J_AB je Coulombická interakce mezi jednotkovými náboji A a B, závislá na jejich vzdálenosti. Derivace celkové energie podle náboje Q_A dává chemický potenciál χ_A, jež je funkcí nábojů: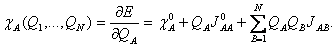

                                                            (27)

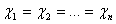                                                                                                                   (28)

Přidáním předpokladu, že součet všech nábojů na jednotlivých atomech je roven celkovému náboji na molekule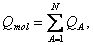

                                                                                                                         (29)

se získá N rovnic pro N nábojů v rovnováze, které se pro danou strukturu řeší [4]. Pro větší modely vzdálené od rovnováhy je obvykle potřeba dříve, než se přiřadí náboje, provést částečnou minimalizaci, protože metoda QEq na deformovaných modelech může vést k výpočtu nerealistických nábojů.

2 Molekulární mechanika

Molekulární mechanika se zaměřuje na statické vlastnosti řešené struktury. Hlavním cílem je optimalizovat geometrii daného modelu, tedy najít uspořádání atomů s minimální celkovou potenciální energií. Pro tuto minimalizaci se ke geometrické optimalizaci souřadnic atomů, a u periodických modelů případně i parametrů buňky, používají různé algoritmy. Další vlastnosti jsou následně počítány z této optimalizované struktury.

Minimalizační algoritmy

Minimalizace modelu probíhá ve dvou krocích. První spočívá ve vyhodnocení výrazu pro energii při daném uspořádání atomů. V druhém kroku je uspořádání upraveno tak, aby mělo nižší hodnotu energie. Minima může být dosaženo po jedné úpravě struktury, nebo může být potřeba tisíce iterací. To závisí na druhu algoritmu, na tvaru plochy energie a na složitosti modelu. Efektivita minimalizace se posuzuje jak časem potřebným k vyhodnocení výrazu pro energii, tak časem a počtem iterací potřebných k dosažení minima. Výraz pro energii je funkce 3N proměnných, kde N je počet atomů v modelu. Každý minimalizační algoritmus musí v tomto 3N-rozměrném prostoru určit směr k minimu a vzdálenost k minimu podél tohoto směru. Nalezený bod určuje souřadnice struktury s nižší energií.

2.1 Metoda největšího spádu (steepest-descents)

Metoda největšího spádu deﬁnuje směr k minimu jako směr gradientu v daném bodě. Tento směr nevede přímo k minimu, proto se v minimu nalezeném podél tohoto směru deﬁnuje gradientem nový směr a iterativně se pokračuje. Minimum podél daného směru se vyskytuje přesně v bodě, v kterém je daný směr tečný k vrstevnicím energie. Z toho vyplývá, že nový směr určený gradientem je kolmý k předešlému. Bez ohledu na to, jakou metodou byl směr k minimu určen, se k hledání minima podél určeného směru často používá metoda, která se nazývá line search. Jedná se o jednodimenzionální minimalizaci podél směrového vektoru, při níž se minimum jednoduše uzávorkovává mezi dva body s vyšší energií. Minima je dosaženo postupnými iteracemi, v nichž se ve směru daného vektoru stále zmenšuje souvislý úsek, v němž se minimum hledá. Fakt, že následující směry jsou na sebe kolmé, zajišťuje efektivní cestu k minimu pro přibližně kvadratické výrazy pro energii. Ovšem ve skutečnosti tato metoda tím, že směr určuje nejstrmějším spádem, a tedy ne nutně přímo k minimu, nejvhodnější směr často mine, což vede k neefektivní trajektorii, která často osciluje kolem cesty k minimu. To se týká ploch energie s úzkými údolími. Tento problém je možno řešit složitějšími algoritmy, jako jsou metoda konjugovaných gradientů a Newtonova-Raphsonova metoda. Dalším problémem je náročnost hledání minima podél určeného směru. Je totiž třeba provést několik (3–10) vyhodnocení výrazu pro energii a v případě molekulární mechaniky bývá vyhodnocení výrazu tou časově nejnáročnější částí výpočtu. Tedy „line search není z tohoto hlediska moc efektivní metoda. Proto se přesné hledání minima neprovádí, ale náhodně se testují body podél prohledávaného směru a nový směr je deﬁnován v prvním bodě, v němž je energie nižší než v bodě výchozím. Výhodou je značný pokles počtu vyhodnocení výrazu během jedné iterace (na 10 %–20 %), přičemž počet iterací k dosažení minima bývá zhruba stejný jako v metodě „line search“, ačkoli trajektorie je více nepravidelná [5]. Metoda největšího spádu bývá v blízkosti minima pomalá. Ovšem vzhledem ke spoléhání se na gradienty je také velmi spolehlivá a silná, bez ohledu na to, jaký tvar má plocha energie nebo z jakého bodu výpočet začíná. Proto se tato metoda obvykle jako první v řadě používá k úvodním úpravám struktur, které jsou daleko od minima a mají velké gradienty, přičemž složitější a soﬁstikovanější algoritmy jsou použity následně.

2.2 Metoda konjugovaných gradientů

Metoda největšího spádu konverguje pomalu v blízkosti minima, protože každý následující směr sice opraví odchylku předešlého směru od ideálního směru k minimu, ale nemůže se mu to účinně podařit vzhledem k podmínce kolmosti k předešlému směru. Metoda konjugovaných gradientů toto omezení nemá a každý následující směr je dán úpravou směru předešlého. V metodě konjugovaných gradientů je nový směrový vektor 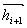 vedoucí z bodu  i+1 dán připočtením gradientu  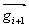v bodě i+1 k předešlému směru 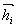přenásobenému konstantou γi :

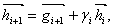                                                                                                                   (30)

kde γi může být deﬁnováno dvěma různými způsoby – v Polakově-Ribiereově metodě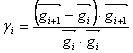

                                                                                                              (31),

a ve Fletcherově-Reevesově metodě [6]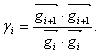

                                                                                                                       (32)

Ačkoli obě metody mají podobné charakteristiky, za různých podmínek může být jedna výhodnější než druhá. Aby bylo zaručeno, že směry jsou vzájemně konjugované, je třeba minimum podél daného směru vyhledat přesně a zajistit tím, že nový gradient bude opravdu kolmý na předešlý směr. Přestože tyto výpočty tak potřebují více vyhodnocení výrazu pro energii, a proto čas na jednu iteraci může být v metodě konjugovaných gradientů delší než v metodě největšího spádu, je tato ztráta více než kompenzována mnohem efektivnější konvergencí k minimu. Je třeba dodat, že tato metoda již předpokládá uspořádání atomů natolik blízko minimu, že plocha energie je už téměř kvadratická, jinak se výpočet může stát nestabilní. Metoda konjugovaných gradientů je vhodná pro velké modely, neboť potřebuje řádově jen N údajů pro uchování předchozího směru (na rozdíl od Newtonovy-Raphsonovy metody, viz dále). Detaily o metodě v [7].

2.3 Newtonova-Raphsonova metoda

Tato metoda navíc k použití gradientu, kterým se určuje směr hledání minima, použije i informaci o zakřivení plochy (druhá derivace) k výpočtu, kde se podél daného směru minimum nachází. Protože matice druhých derivací výrazu pro energii A deﬁnuje zakřivení v každém směru, přenásobením její inverze A⁻¹(r₀ ) gradientem ∇E(r₀ ) ve výchozím bodě r₀ lze vypočíst předpokládané minimum r_min :

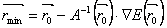                                                                                                      (33)

Obdobně jako v předešlých metodách je třeba provádět tento postup iterativně. Nevýhoda této metody je, že výpočet matice druhých derivací je časově náročný a vzhledem k řádovým rozměrům N² nemusí být pro velké systémy výpočetní technikou zvládnutelný. Tato metoda je ještě citlivější než metoda konjugovaných gradientů na požadavek kvadratičnosti plochy energie, v opačném případě je nestabilní. Proto se obvykle používá až jako poslední z minimalizačních algoritmů pro případ, kdy je požadována extrémní přesnost na dosažené minimum, např. pro následný výpočet vibračních frekvencí, které jsou vypočteny chybně i v případě malých zbytkových gradientů. Existují různé variace Newtonovy-Raphsonovy metody, např. kvasi-Newtonova metoda, „oříznutá Newtonova metoda, atd. Některé z nich mají výhodu, že nepotřebují k uchování N² údajů pro matici druhých derivací.

Literatura

1.     P. Comba, T. W. Hambley, Molecular Modeling of Inorganic Compounds. VCH, Weinheim, 1995.

2.     M. Veteška, Molekulární simulace ve strukturní analýze interkalátů. MFF UK Praha, 2006

3.     N. Karasawa, W. A. Goddard III, J. Phys. Chem. 93 (1989), 7320-7327.

4.    A. K. Rappé, W. A. Goddard, J. Phys. Chem. 95 (1991), 3358.

5.    M. Levitt, S. Lifson, J. Molec. Biol. 46 (1969), 269

6.    R. Fletcher, C. M. Reeves, Comput. J. 7 (1964), 149.

7.   R. Fletcher, Practical Methods of Optimization, Vol. 1, Unconstrained Optimization. John Wiley&Sons, New York, 1980.