Fe₂O₃/SiO₂ Nanocomposite – Shape of the e-Fe₂O₃ Nanocrystals

P. Brázda¹, M. Klementová¹ and D. Nižňanský²

¹Institute of Inorganic Chemistry of the AS CR, v.v.i., 250 68 Husinec-Řež 1001, Czech Republic

²Dept. Inorg. Chem., Faculty of Science, Charles University in Prague, Hlavova 8,
12843 Prague 2, Czech Republic

brazda@iic.cas.cz

The first article dealing with the e-Fe₂O₃ was published in 1934 [1]. However, its crystal structure described in the orthorhombic Pna2₁ was published in 1998 [2]. The structure of epsilon phase is characterized by the closest packing of the oxygen anions with ABAC stacking. The stacking planes are parallel to (001). The iron cations occupy four different sites. Three of them have octahedral and the last one has tetrahedral coordination polyhedron. The values of the lattice constants are a = 5.091 Å, b = 8.784 Å and c = 9.472 Å. After a discovery of its giant 2 T room temperature coercivity in 2005 [3] the epsilon phase attracted more attention as these properties predestinates it as a promising material for magnetic recording and information storage. Moreover, in 2009 Namai et al. used this phase as a high-performance millimeter electromagnetic wave absorber, which opens a possibility of the applications of this material in high-speed wireless communication devices [4].

Nanocomposites were prepared by a sol-gel process using complex molecule of ferric cation and organic molecule H₂L bearing two trimethoxysilyl groups (H₂L = bis-[3‑(trimethoxysilyl)propylamide] of ethylenediaminetetraacetic acid). After hydrolysis and condensation of Si-OMe groups followed by drying, the xerogels obtained were annealed at final temperatures between 900 to1100 °C, thus obtaining nanocomposites with 40% weight concentration of iron oxide [5]. The SiO₂ matrix was removed by reacting the nanocomposite with 5 M NaOH at 80 °C for three days. The nanocrystals were then washed several times by distilled water and collected by centrifugation. The transmission electron microscopy (TEM) measurements were conducted using a JEOL JEM-3010, while the X-ray diffraction (XRD) data were collected using a PANalytical X’Pert Pro with Cu K_a radiation (λ = 1.5418 Å) at room temperature with the 2θ range between 10° and 110°. Rietveld analyses were performed by the Fullprof program [6]. As a profile function was used Thompson-Cox-Hastings pseudo-Voigt function. For a modeling of the anisotropic shape of the crystallites were used spherical harmonics.

The epsilon phase is stable only in a restricted size range between approximately 10 to 100 nm. It crystallizes in the Fe₂O₃/SiO₂ system from maghemite and transforms to thermodynamically stable hematite under prolonged heat treatment. The shape of the epsilon phase crystals depends on the size of the crystals. The particles obtained at 1100 °C adopt a disc-like shape flattened in c direction with similar diameters in a and b directions and they are in almost all cases single crystals. The largest crystal faces are (001) and (110) as deduced from the HR-TEM images. These results are in an agreement with XRD data fitting (Figure 1). Table 1 summarizes the volume weighted diameters in the [100], [010] and [001] of the coherently diffracting domains of the epsilon phase. The fastest growth of the crystals in the temperature range between 900 °C and 1100 °C is in the [001] followed by the [100]. The smallest growth is in the [010]. It is important to note that the viscosity of the silica matrix significantly increases at about 1000 °C. Under this temperature the growth of the particles is much slower. To understand this anisotropic growth of the epsilon crystals it is necessary to understand the basics of the epsilon transformation from maghemite.

Maghemite has a spinel structure, which is described in the cubic space group . The stacking of the oxygen anion layers is along <111>. The maghemite particles with the size close to 10 nm are flattened in one of the <111> directions (Figure 2). Some particles contain domains of both maghemite and epsilon. The contact plane of these phases was found to be <111>_M/[001]_e. Evaluation of the FFTs of the HR-TEM images showed that there is a fixed structural orientation relationship between these two phases (<110>_M is parallel to [010] _e and <211>_M is parallel to [100]_e, Figure 3). This orientation relationship is the same as that found by Ding et al. for magnetite and epsilon [7]. Interestingly, the nanowires of magnetite described in this work transformed in the epsilon phase only in case when the nanowires grew along one of the <110> of magnetite (which is the same direction as the <110> of maghemite), which could explain why is the largest diameter of the smallest epsilon particles is in the [010]_e.

In conclusion the transformation of maghemite to epsilon is probably much faster within a cationic layer than in the direction perpendicular to the atom stacking as evidenced by the different growing rate of the epsilon phase in the a, b and c directions.

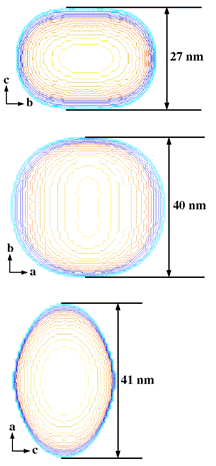
Figure 1 Comparison of modeled anisotropic crystal shape (left) with crystals viewed along the corresponding directions in the HR-TEM images (right) of the sample annealed at 1100 °C.

Figure 2 HR-TEM image of a maghemite particle observed along <211> direction.

Figure 3 HR-TEM image of a particle containing both maghemite and epsilon. Arrow points in [111]_M and [001]_e. Perpendicular to this direction is <110>_M//[010]_e.

Table 1 Volume weighted diameters on e-Fe₂O₃ as a function of the annealing temperature.

Temperature (°C)	[100] (nm)	[010] (nm)	[001] (nm)
900	6(1)	11(1)	3(1)
950	10(1)	10(1)	5(1)
1050	28(2)	24(2)	17(2)
1100	41(3)	40(3)	27(3)

1. H. Forestier & G. Guiot-Guillain, C. R. Acad. Sci. (Paris), 199 (1934) 720

2. E. Tronc, C. Chanéac & J. P. Jolivet, J. Solid State Chem., 139 (1998) 93-104

3. J. Jin, K. Hashimoto & S. Ohkoshi, J. Mater. Chem., 15 (2005) 1067-1071

4. A. Namai, S. Sakurai, M. Nakajima, T. Suemoto, K. Matsumoto, M. Goto, S. Sasaki & S. Ohkoshi, J. Am. Chem. Soc., 131(3) (2009) 1170-1173

5. P. Brázda, D. Nižňanský, J.-L. Rehspringer & J. Poltierová Vejpravová, J. Sol‑Gel Sci. Technol., 51 (2009) 78-83

6. J. Rodriguez-Carvajal, Physica B, 192 (1993) 55-69

7. Y. Ding, J. R. Morber, R. L. Snyder & Z. L., Wang Adv. Funct. Mater., 17 (2007) 1172-1178