Metoda dvou záření na určení velikosti krystalitů a mikrodeformací
M. Čerňanský
Fyzikální ústav AV ČR, v. v. i., Na Slovance 2, 182 21 Praha 8, Česká republika
cernan@fzu.cz
Je obecně známo, že malá velikost krystalických částic – pod 1 μm – způsobuje rozšíření difrakčního profilu dané Scherrerovým vzorcem [1]
![]()
kde β je rozšíření difrakční
linie (v radiánech), způsobené malou velikostí krystalických částic D (ve směru kolmém na difraktující roviny), θ
je difrakční úhel, λ vlnová délka, K je Scherrerova
konstanta, závislá na tvaru částic a její hodnota je blízká 1. Podobně je známo, že
mikrodeformace o velikosti e = Δd/d (d je mezirovinná
vzdálenost) vyvolají rozšíření difrakční linie [1]
![]()
Obě příčiny rozšíření linií působí
velmi často současně, takže k určení velikosti částic a mikrodeformací je
nutné kvantitativně stanovit, jak velkou část fyzikálního rozšíření způsobuje
velikost částic a jaký podíl
na něm mají mikrodeformace. K tomuto účelu se obvykle využívá té
skutečnosti, že zmíněné příčiny rozšíření závisejí na difrakčním úhlu θ různým způsobem. Podle rovnice (1) je to pro
velikost částic funkce sec θ = (1/ cos
θ) a podle rovnice (2) pro mikrodeformace je to funkce tg θ.
Tyto funkce se však výrazně liší (Obr. 1) jen u malých úhlů θ,
kde obvykle není dostatečný počet difrakčních linií a jejichž šířky jsou malé,
jsou blízké šířkám přístrojové
funkce, takže jejich určení je značně nepřesné.
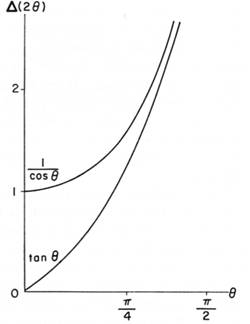
Obrázek 1. Závislosti
difrakčních rozšíření na úhlu θ.
Naneštěstí u velkých hodnot θ, kde jsou rozšíření od malé velikosti částic i od mikrodeformací dost velká a dají se poměrně presně měřit, mají obě funkce – sec θ = 1/cosθ a tgθ – podobný průběh (Obr. 1), takže možnost rozlišit, co je způsobeno velikosti částic a co mikrodeformacemi, se zmenšuje. Navíc u velkých hodnot θ vadí velké rozšíření měřené linie od nenulové délky spektrálního intervalu Δλ, které je
![]() .
(3)
.
(3)
Spektrální složka instrumentální funkce tedy roste s růstem θ a tím snižuje přesnost v určení fyzikálního profilu. Z tohoto důvodu se doporučuje určovat velikost částic – a mikrodeformací - spíše u malých úhlu θ [2].
Wood [3] proto navrhnul využít tu skutečnost, že při stejném difrakčním úhlu θ, je rozšíření od malé velikosti částic přímo úměrné vlnové délce λ, zatímco rozšíření od mikrodeformací na λ nezávisí, jak to plyne z rovnic (1) a (2). Porovnají se tedy šířky dvou (různých) difrakčních linií se stejným úhlem θ na difraktogramech zkoumaného vzorku získaných se zářením o dvou různých vlnových délkách, např. λ1 = 0.154 nm (měď) a λ2 = 0.071 nm (molybden). Jsou-li šířky linií stejné, je rozšíření nezávislé na vlnové délce a je tedy způsobeno mikrodeformacemi. Pokud je rozšíření vyvolané malou velikostí částic, bude šířka linie přibližně dvakrát větší pro záření mědi, než pro záření molybdenu - pokud lze zanedbat přístrojové rozšíření – [4]. Tento kvalitativní přístup byl použitý ke sledování struktury oceli [3].
Je však možné odvodit kvantitativní,
explicitní vyjádření pro velikost částic a mikrodeformací, určených metodou
dvou záření. Jako u Williamsonova – Hallova grafu předpokládejme, že rozšíření
od velikosti částic a od mikrodeformací se jednoduše sčítají, tj. pro měření
s vlnovými délkami λ1 a λ2 platí rovnice
![]() (4)
(4)
a
![]()
![]() ,
(5)
,
(5)
kde na levých stranách
jsou šířky difrakčních linií po korekci na přístrojové rozšíření. Rovnice (4) a
(5) tvoří soustavu dvou rovnic o dvou neznámých, D a e. Řešením
této soustavy dostáváme pro velikost částic
![]() (6)
(6)
a pro velikost
mikrodeformací
![]() (7)
(7)
Z rovnice (4) nebo (5)
ještě plyne grafická verze této metody – analogie Williamsonova – Hallova
grafu, pro více než dvě záření
![]() .
(8)
.
(8)
Když tedy vyneseme
závislost ![]() na
na ![]() , dostaneme přímku se směrnicí
, dostaneme přímku se směrnicí ![]() , která na ose y vytíná úsek
, která na ose y vytíná úsek ![]() .
.
References
1. H.P. Klug & L.E. Alexander, X-Ray Diffraction Procedures for Polycrystalline and Amorphous Materials. New York 1974. Wiley, 2nd ed.
2. A. Guinier, X-Ray Diffraction. San Francisco and London 1963. Freeman.
3. W.A. Wood, Nature, 151 (1943) 585.
4. A. Kochanovská, Strukturní rentgenografie, Praha 1964. SNTL.
Poděkování. Tato práce vznikla v rámci realizace projektu Akademie věd České republiky - KAN 300100801.