XRD study of thickness dependence of crystallization and stresses of TiO₂ thin films

L. Nichtová, R. Kužel, Z. Matěj

Department of Condensed Matter Physics, Facuty of Mathematics and Physics, Charles University in Prague, 121 16 Praha 2, Czech Republic

nichtova@email.cz

Titanium dioxide is a material intensively investigated not only because of its good chemical stability, mechanical hardness, high refractive index and nontoxicity but also due to its photocatalytic activity enabling a conversion of solar light into useful chemical energy. It is known that photocatalytic activity of titanium dioxide strongly depends on crystallization and phase composition.

In this work a complex x-ray diffraction (XRD) study of thin TiO₂ films on Si substrates with different thicknesses (50−2000 nm) prepared by magnetron sputtering is presented. Crystallisation process of amorphous films was studied in-situ. XRD reflectivity, texture and stress measurements were performed ex‑situ. Other amorphous and nanocrystalline powders were also measured for comparison.

In-situ xrd measurements were done with the aid of X’Pert Pro diffractometer with MRI high-temperature chamber. Annealing temperatures were selected below the temperature where fast crystallization appears (about 220 °C). The process is then slow and allows detailed time in-situ investigations even in laboratory conditions. Strong dependence of crystallization kinetics on the film thickness was found. In particular for the samples with thickness lower than 300 nm. The process could be well described by the Avrami equation [1] (modified by the introduction of initial time of crystallization). The evolution of the integrated intensities I (Figure 1) of diffraction lines of anatase phase is then described as, I = 1-exp[-b(t–t₀)ⁿ)], where the initial time of crystallization t₀ is related to the first appearance of any diffracted intensity above the background level at the peak position. It increases abruptly with decreasing thickness. The rate of crystallization b grows quickly with the thickness. Low values of n (~ 2) indicate two-dimensional character of the crystallite growth. Changes of preferred orientation and stress generation during the crystallization were observed.

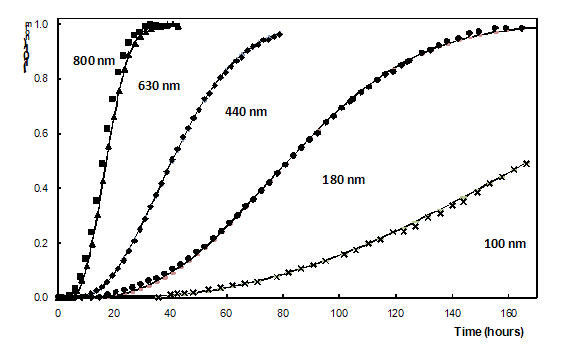
Figure 1. Normalized integrated intensity of anatase diffraction peak 101 in dependence on annealing time (annealing temperature 180 °C) for films of different thickness (symbols … experimental values, lines … fitted Avrami equations)

Tensile residual stresses were developed slowly during the crystallization and confirmed later by detailed measurements at room temperature. In the first step, the stress measurements were analysed with X'Pert Stress program by means of the d_hkl vs. sin ²y plots. Slopes and intercepts of the sin ²y plots were obtained. In the second step, the stress values were determined from the analysis of all the reflections assuming symmetrical bi-axial state of the residual stress and the weighted Reuss- Voigt grain interaction model [2]. Figure 2 shows obtained and calculated slopes divided by the corresponding intercepts of the sin ²y plots for all measured reflections for the sample with thickness 440 nm annealed at 200 °C. Systematic anisotropy, observed for all investigated samples, can be well described by the weighted Reuss-Voigt model using single crystal elastic constants of anatase [3] which recently appeared. The anisotropy is completely different for rutile – the second phase of tetragonal TiO_2. Figure 3 shows relative deviation of obtained and calculated sin ²y intercepts. Deviations are rather small, comparable with the rounding error of the intercepts values in the X'Pert Stress program. Rapidly increasing value of residual stress with decreasing film thickness was observed (Figure 4).

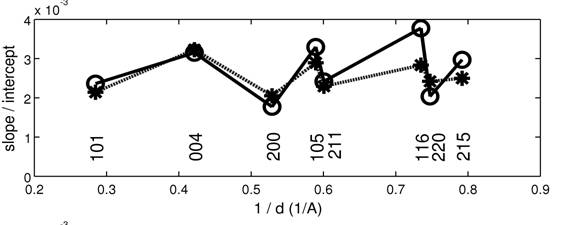
Figure 2. Comparison of slopes divided by corresponding intercepts of the sin ²y plots for the 440 nm thin film sample (o) and simulated XECs anisotropy dependence (*).

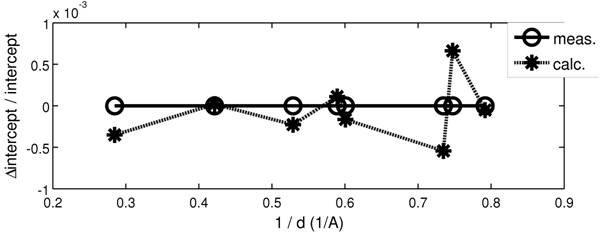
Figure 3. Relative differences of intercepts of sin ²y plots for the 440 nm thin film sample (o) and simulated data (*).

Figure 4. Film thickness dependence of the residual stress.

[1] M. J. Avrami, J. Chem. Phys. 7 1103 (1939)

[2] M. Dopita, D. Rafaja, Z. Kristallogr. Suppl. 23 (2006) 67-72

[3] M. Iuga, G. Steinle-Neumann, J. Meinhardt, Eur. Phys. J. B 58 (2007) 127-133