Standing-wave-grazing-incidence x-ray diffraction from polycrystalline multilayers

J. Krčmář¹, V. Holý², I. Vávra³

¹1Institute of Condensed Matter Physics, Masaryk University, Koltářská 2, 611 37 Brno, Czech Republic

²Department of Physics of Electronic Structures, Charles University, Ke Karlovu 5, 121 16 Prague, Czech Republic

³Institute of Electrical Engineering Slovak Academy of Sciences, Dúbravská cesta 9, 84239 Bratislava, Slovak Republic

krcmar@physics.muni.cz

In work [1] authors presented a new diffraction method, which uses the concept of x-ray standing wave in the grazing-incidence geometry, in which both the incidence and exit angles a_i,f are close to the critical angle a_c of total external reflection. If the angle of incidence a_i of the primary x-ray wave onto a periodic multilayer is close to a_i or to a “Bragg-like” maximum on the reflectivity curve, the interference of the transmitted and reflected waves creates a standing wave pattern in the multilayer volume, the period of which equals the multilayer period. If the multilayer contains crystalline grains (crystallites), the intensity of diffraction from these crystallites depends on the mutual position of the crystallites and the antinodes of the standing wave. Similarly, the wave diffracted by the crystallites is reflected from the multilayer interfaces, which results in a standing wave pattern as well. The standing wave pattern is shifted by changing a_i or a_f so that from the measured dependence of the diffracted intensity on a_i,f it is possible to determine the position of the diffracting crystallites. Moreover, measuring the dependences of the diffracted intensity on the in-plane scattering angle 2q at various a_i it is possible to determine the lateral sizes of the crystallites in different depths in the multilayer. The theoretical description of the scattering process is based on the Distorted-Wave Born approximation.

In Ref. [2], we proved the feasibility of this concept by measuring the standing-wave effects in C/Ni₃N multilayers using synchrotron radiation, and we were able to determine the sizes of the crystallites in different depths in the multilayer and the thicknesses of amorphous Ni₃N transition layers at the C/Ni₃N interfaces.

In Ref. [3], we demonstrate that this method can be carried out also at a modified x-ray diffractometer (Figure (1)), and it is capable of studying the structure of crystalline layers in a periodic multilayer at a laboratory (Figure (2)). We have used this method for the investigation of the structure of Nb/Si multilayers, and we obtained the thicknesses of amorphous and crystalline parts of the Nb layers. These thicknesses agree very well with the transmission electron microscopy observations.

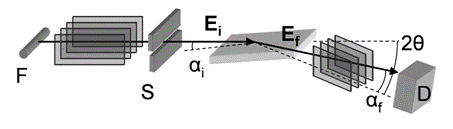
Figure 1. The geometry of the experimental method in the laboratory. X-ray tube has line focus F parallel to the surface plane. The incident E_i beam is restricted by a parallel plate collimator and slit S. The scattered beam E_f is restricted by a second parallel plate collimator. 2q is the scattering angle and a_i and a_f are the incident and exit angles with respect to the sample surface.

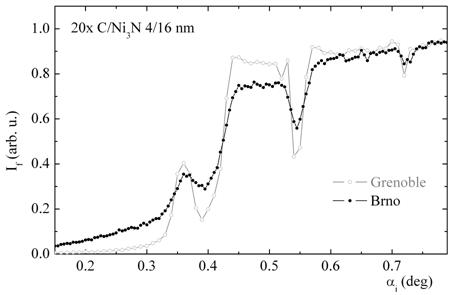
Figure 2. Diffraction measured in the laboratory (Brno) and at the ID01 beamline at ESRF (Grenoble).

From the fits, it follows that the Nb layer consists in an amorphous part of the thickness of 2.0±0.5 nm lying at the Si/Nb interface (i.e., in the bottom part of the Nb layer) and of the crystalline part in the upper part of the layer at the Nb/Si interface. Figure (3) shows the comparison of the measured and fitted intensity curves. To demonstrate the sensitivity of the method, in Fig. (3) we have also plotted the calculated diffraction curves assuming that whole Nb layers are crystalline (dashed lines). From the figure, it is obvious that the agreement of these curves with the experimental data is much worse and the method is capable indeed to measure the thickness of the amorphous part of the Nb layer.

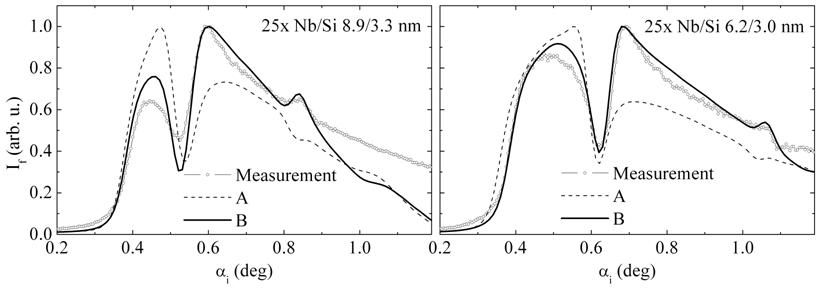
Figure 3. Measured (points) and fitted (lines and dash line) diffraction intensities. Curve A: all volume of Nb layers is crystalline. Curve B: bottom 2 nm thick parts of the Nb layers are amorphous.

Presented method is very suitable for a detailed study of sizes and positions of crystallites in periodic multilayers, as well as for the determination of the depth profile of the crystallite size.

References

1. P.F. Fewster, N.L. Andrew, V. Holý, K. Barmak, Phys. Rev. B., 72, (2005) 174105.

2. J. Krčmář, V. Holý, L. Horák, T.H. Metzger, J. Sobota, J. Appl. Phys., 103, (2008) 033504.

3. J. Krčmář, V. Holý, I. Vávra, Appl. Phys. Lett., 94, (2009) 101909.