Poznámky k momentům difrakčních profilů

 

M. Čerňanský

 

Fyzikální ústav AV ČR, v. v. i., Na Slovance 2, 182 21 Praha 8, Česká republika

 

Na předchozím kolokviu ve Valticích bylo upozorněno na některé vlastnosti kumulantů, které lze velmi výhodně využít při analýze profilů difrakčních linií [1]. Zde se konkrétně jedná o poznatek, že pro kumulantyfunkcí v konvoluci h = f  * g platí pro všechy řády n [2, 3]

 

                                                          .                                                                     (1)

 

Tato vlastnost kumulantů umožňuje velmi jasně formulovat již známou metodu čtvrtých momentů k určení velikosti částic D a mikrodeformací ε z profilu jedné difrakční linie [4]. Předpokládáme, že profily f D a f ε po řadě odpovídají velikosti částic D a mikrodeformaci a že fyzikální profil f je konvolucí profilů f D, f ε. Podle (1) pak lze druhý a čtvrtý kumulant fyzikálního profilu f  napsat ve tvarech

 

                                                                                                                                   (2)      

a   

                                                               ,                                                                   (3)   

 

kde κ2D a κ4D jsou druhý a čtvrtý kumulant profilu f D, podobně κ2ε a κ4ε  jsou druhý a čtvrtý kumulant profilu f ε. Z obecných vztahů mezi kumulanty a centrálními momenty [5]

 

                                                                                                                                               (4)

                                               

                                                                                                                                     (5)

 

pak vychází

 

                                                 ,                                                      (6)

 a    

                                                 ,                       .                                 (7)

 

Rovnice (2) a (3) tvoří soustavu dvou rovnic pro dvě neznámé – velikost částic D a mikrodeformací ε. Tyto neznámé se v (2) a (3) explicitně objeví po dosazení centrálních momentů z pravých stran v (6) a (7). Existuje totiž  vztah [6]

 

                                                  ,                                                            (8)                                                                                                                    

 

kde W je variance, t.j. druhý centrální moment μ2D profilu f D, k je faktor tvaru částic a Millerových indexů, Δ(2θ) je úhlový interval pro výpočet variance, λ je vlnová délka a θ0 je Braggův úhel. Podobně profil  f ε

má druhý centrální moment [6]

 

                                                       .                                                                         (9)

 

Než se provede zmíněné dosazení, je dobré si uvědomit následující skutečnosti. Obvykle se o profilu f ε

předpokládá, že má Gaussův tvar [7]. Navíc bylo ukázáno, že čtvrtý kumulant Gaussovy funkce je roven nule [8]. Tyto skutečnosti vedou k podstatnému zjednodušení při řešení soustavy rovnic (2) a (3) pro neznámou velikost částic D a neznámou mikrodeformaci ε.

     Ukazuje se, že důležité jsou zejména dva případy: a) čtvrtý centrální moment profilu f D od velikosti částic je přímo úměrný druhému centrálnímu momentu tohoto profilu, b) čtvrtý centrální moment profilu f D je přímo úměrný druhé mocnině druhého centrálního momentu tohoto profilu. Pomocí první věty integrálního počtu o střední hodnotě [9] se dá obecně dokázat, že nastává varianta a). Zmíněná věta zní: Jsou-li funkce f(x) a g(x) v intervalu <a, b> spojité a má-li funkce g(x) v tomto intervalu stále totéž znaménko, platí

 

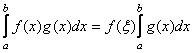
                                                                     pro    ,           (10)

 

kde ξ je hodnota z intervalu (a, b). Dosadíme tedy f(x) = x2 a g(x) = x2 φ(x), kde φ(x) je profil difrakční linie.  Předpoklady věty jsou evidentně splněny, takže podle definice druhého a čtvrtého centrálního momentu vychází

 

                                                                                                                                           (11)

 

Pro Gaussovu křivku sice platí

                                                       ,                                                                                 (12)

 

ale nemůžeme předpokládat, že oba profily, f D, f ε současně mají Gaussův tvar, protože to by při řešení soustavy (2), (3) vedlo k neurčitým výrazům typu 0/0.

                                                      

     Druhá poznámka se týká tvaru závislosti momentu profilu f D od velikosti částic D na této veličině (D). Podle známého Wilsonova vzorce (8) je variance profilu f D nepřímo úměrná velikosti částic D. Variance je podle definice druhým centrálním momentem profilu. Profil od velikosti částic má často tvar [10]

 

                                                       ,                                                               (13)

 

kde s = 2 sin /je proměnná profilu v reciprokém prostoru a M je počet difraktujících rovin ve směru kolmém na tyto roviny. Velikost částic D je zřejmě M – násobkem příslušné mezirovinné vzdálenosti. Přímý výpočet variance profilu f (s), daného rovnicí (13), podle definice z matematické statistiky [5], dává

 

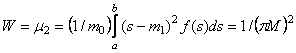                                                        ,                          (5)

 

kde m0 je v našem případě integrální intenzita a m1 těžiště profilu. V tomto případě tedy vychází, že variance profilu od velikosti částic je nepřímo úměrná druhé mocnině velikosti částic.

 

 

[1] M. Čerňanský: Materials Structure, 15 (2008) k45-k46.

[2] A.C. Aitken: Statistical Mathematics. Edinburgh and London 1947. Oliver and Boyd.

[3] L. Janossy: Theory and Practice of the Evaluation of Measurements. Oxford 1965. Oxford

      University Press.

[4] A.S. Kagan & V.M. Snovidov: Fizika metallov i metallovedenije, 19 (1965) 191-198.

[5] H. Cramér: Mathematical Methods of Statistics. Princeton 1946. Princeton University Press.

[6] H.P. Klug & L.E. Alexander: X-Ray Diffraction Procedures for Polycrystalline and Amorphous

      Materials. New York 1974. Wiley, 2nd ed.

[7] B.E. Warren: Prog. Met. Phys. 8, (1959) 147-202. Eds. B. Chalmers & R. King. London: 

      Pergamon  Press. Ruský překlad Usp. Fiz. Met. 5 (1963) 172-237.

[8] M. Čerňanský: Zeit. Kristallogr. Supplement No. 27 (2008) 127-133.

[9] H.-J. Bartsch: Matematické vzorce. Praha 1983. SNTL.

[10] Guinier, A. (1963). X-Ray Diffraction. San Francisco and London 1963. Freeman.

 

Poděkování. Tato práce vznikla v rámci realizace projektu Grantové agentury České republiky, číslo 106/07/0805.