Refinement of magnetic structures in Jana2006
V. Petříček and M. Dušek
Institute of Physics
of the ASCR, v. v. i.,
Na Slovance 2
CZ-182 21 Praha 8,
petricek@fzu.cz
Keywords: crystal structure analysis, magnetic structures, modulated structures
The program Jana is well known system for solution and refinement of regular, modulated and composite crystals. Jana was originally oriented to data collected from a single crystal with a wide support for handling of twinning. In the version Jana2000 the program was generalized for structure refinement from powder data including multiphase option [1]. Finally the multiphase option has been generalized for a single crystal refinement.
During the year 2006 the old code of Jana2000 has been completely rewritten in order to open possibility for adding various new options. Probably the most important change is the option for making joint refinements from different data collections. Thus data sets from powder and single crystal measured with X-rays and neutrons can be used simultaneously.
The magnetic scattering formalism has been implemented recently. The program can be used not only for structures having nuclear and magnetic lattices identical but also for commensurate and incommensurate magnetic and nuclear arrangements. For this reason we have generalized concept of superspace groups, as introduced by Janner, Janssen and de Wolff [2], to magnetic groups. Such an approach has following advantages:
· Simple relationship to the Laue diffraction group facilitates symmetry recognition
· The magnetic structure can be handled even for regularly modulated and composite crystals
· The general modulation wave can account for complicated magnetic modulation – more harmonics, step like modulations, …
The only disadvantage is that the new formalism may be too complicated for people without an experience with superspace description.
Calculation of magnetic structure factor, which is generally a vector, is based on the general equation:
where p
is a normalization constant to transfer magnetic scattering calculated in Bohr
magnetos to the scale used for nuclear neutron structure factors, 
magnetic form
factor, 
is the ADP
(temperature) factor and 
is the magnetic
moment of the ith atom.
The geometrical part 
is a function
of the atom position
. Intensity of a magnetic reflection is related to the
square length of the magnetic structure factor projected into the reflection
plane:
The intensity of the magnetic reflection combines with the intensity originating from the nuclear scattering. The combination is made as from independent object (twins):
The magnetic moments of atoms can follow the same translation periodicity of the nuclear structure or they can have their own periodicity either commensurate or incommensurate with the nuclear lattice. Generally the magnetic moment can be written as a combination of harmonic functions:
The superspace approach does not give a direct connection to irreducible representation analysis, as introduced by E.F. Bertaut [3]. For this reason we have also implemented a tool which can directly perform such an analysis in the Jana package. This part of the program is analogical to programs such as MODY [4], SARAh [5] and BasIReps [6]. New contribution of Jana is that the result of the representative analysis is transformed (see example in the Fig.1) into (super)space magnetic group. Moreover all additional conditions (if any) necessary to assure selected irreducible representation are generated automatically and used during the refinement process. This makes possible to test all acceptable irreducible representation directly in terms of Laue symmetry and systematic extinctions.
The refined magnetic structure can be visualized by calling a suitable external drawing program from Jana2006. In the Fig.2 an example of a refined magnetic structure is drawn by Diamond 3.0 [7].
The program has been already tested on
several data sets from different sources (
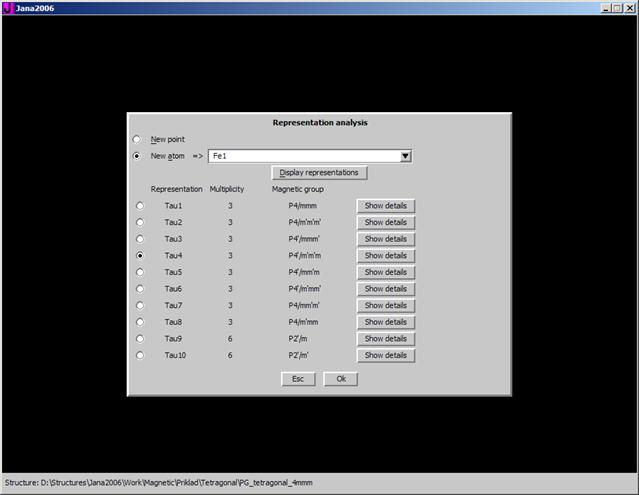
Figure 1. The
pilot window for representative analysis for the space group 
.
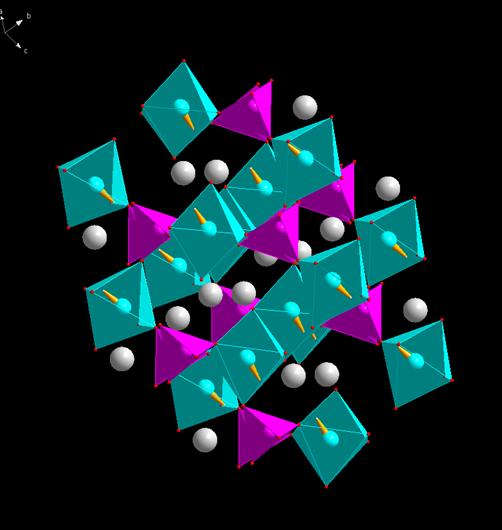
Figure 2. The magnetic ordering for BiNPO5 as refined by Jana2006
References
1.
M. Dušek, V. Petříček, M. Wunschel, R.
E. Dinnebier, S. van Smaalen, J.
Appl.Cryst., 34, (2001). 398.
2. P.M. de Wolf, T.Janssen, A.Janner A., Acta Cryst. A37, (1981), 625.
3. E.F. Bertaut, Acta Cryst.. A24, (1968) 217.
4. P. Czapnik, W. Sikora, http://www.ftj.agh.edu.pl/~sikora/modyopis.htm
5. A.S.Wills, Physica B, 276, (2000), 680.
6. J. Rodriguez-Carvajal, http://www.ill.eu/sites/fullprof/php/reference.html
7.
K.Brandemburg, Diamond