Kumulanty v
profilové analýze
M. Čerňanský
Fyzikální ústav AV ČR, v.v.i., Na Slovance 2, 182 21 Praha 8, Česká republika
Kumulanty, resp. semiinvarianty jsou po momentech dalším pojmem z teorie
pravděpodobnosti a matematické statistiky, které lze výhodně využít při analýze
profilů difrakčních linií. Obvykle se definují následujícím způsobem:
Označme f(x) jako hustotu (rozložení) pravděpodobnosti náhodné proměnné x.
Jinými slovy, pravděpodobnost toho, že náhodná proměnná x je z intervalu
(x, x + dx) je f(x)d(x) a zřejmě platí podmínka pro
normování pravděpodobnosti
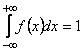 .
(1)
.
(1)
K hustotě pravděpodobnosti f(x) se v případě spojité
náhodné proměnné x definuje, např. [1, 2], pravděpodobnostní vytvořující funkce G(t) = G(t; f) vztahem
![]() .
(2)
.
(2)
Položíme-li v (2) t = ea, obdržíme momentovou vytvořující funkci
![]() = M(a) (3)
= M(a) (3)
a rozvojem logaritmu momentové vytvořující funkce M(a)
dostáváme vytvořující funkci kumulantů
![]() , (4)
, (4)
kde κn jsou kumulanty hustoty pravděpodobnosti f(x).
V praxi se většinou kumulanty
počítají z momentů pomocí rekurentního vztahu
![]() ,
(5)
,
(5)
kde mn
jsou momenty kolem počátku
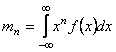 , n
= 0, 1,… (6)
, n
= 0, 1,… (6)
Číslo n je řád momentu nebo
kumulantu. Speciálně
κ1 = m1, t.j.
první kumulant je roven těžišti rozložení f(x). Pro
další kumulanty pak z (5) vychází
![]() (7)
(7)
![]() (8)
(8)
![]() , (9)
, (9)
![]() ...
(10)
...
(10)
Vztahy pro výpočet kumulantů z centrálních momentů
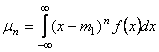 , n
= 0, 1,…
(11)
, n
= 0, 1,…
(11)
jsou zřetelně jednodušší
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
a
vidíme, že druhý kumulant je roven varianci funkce f(x).
Při analýze difrakčních profilů jsou
nejužitečnější ty vlastnosti kumulantů, které souvisí s konvolucí. Je známo, že
těžiště konvoluce h =f * g je součtem těžišť funkcí f a g a
totéž platí pro variance [3]. Stejně jednoduchý vztah platí ještě pro třetí
centrální momenty, ale pro momenty vyšších řádů platí složitější vztah [4]
![]() .
(15)
.
(15)
Naproti
tomu pro kumulanty funkcí v konvoluci h =f * g platí pro všechny řády n
[1, 5]
![]() (16)
(16)
Dále mají kumulanty velmi cennou
vlastnost u vícenásobné
konvoluce h = p * q * r * s * t... [5]
![]() , (17)
, (17)
která byla navržena k analýze kombinace jednotlivých geometrických aberací
způsobených nedokonalostí přístroje [6].
Kumulanty byly použity rovněž při interpretaci fyzikálních profilů [7],
zejména při analýze metody čtvrtých momentů na určení velikosti krystalitů a
mikrodeformací z jedné linie [8 - 10].
Ze
snadno vypočtených kumulantů lze přímo nebo pomocí momentů vypočíst hledanou
funkci, např. fyzikální profil f. K tomu lze použít vztahy [11, 12]
inverzní k rovnicím typu (14)
![]() (18)
(18)
a pak použít např. Edgeworthovu řadu [7, 11], nebo Grammovu-Charlierovu řadu [7, 12], přičemž počet členů může být
malý. Zpravidla stačí rozvoj do čtvrtého momentu [11].
[1] A.C. Aitken: Statistical Mathematics. Edinburgh and London 1947. Oliver and Boyd.
[2] J. Hátle & J. Kahounová: Úvod
do teorie pravděpodobnosti. Praha 1987. SNTL/Alfa.
[3] A.J.C. Wilson: Mathematical Theory of
X-Ray Powder Diffractometry. Eindhoven 1963.
Philips Technical Library.
[4] A. Fingerland: Czech J. Phys. B 10
(1960) 233-239.
[5] L. Janossy: Theory and Practice of the
Evaluation of Measurements. Oxford 1965. Oxford
University Press.
[6] A.J.C. Wilson: J. Appl. Cryst. 6
(1973) 230-237.
[7] M. Čerňanský: Z. Kristallogr. v tisku.
[8] A.S. Kagan & V.M. Snovidov, Fizika metallov i
metallovedenije, 19 (1965) 191-198.
[9] V.M. Snovidov, A.S. Kagan & A.E.
Kovalskii: Zav. Lab. 34 (1968) 1086-1088.
[10] J. Neumann & M. Čermák, Čs.
čas. fyz. A 27 (1977) 601-603.
[11] H. Cramér: Mathematical
Methods of Statistics. Princeton 1946. Princeton University Press.
[12] M.G. Kendall & A.
Stuart: The Advanced Theory of Statistics, Vol. 1. London 1969. Charles
Griffin.
Poděkování. Tato práce vznikla v rámci realizace projektu
Grantové agentury České republiky, číslo 106/07/0805.