Combined X-ray powder diffraction and DFT calculation to elucidate molecular and crystal structure of fluorostyrenes

Microstructure analysis of nanocrystalline materials and nanocomposites using the combination of X-ray diffraction and transmission electron microscopy

D. Rafaja¹, V. Klemm¹, C. Wüstefeld¹, M. Motylenko¹, M. Dopita^1,2

¹Institute of Materials Science, TU Bergakademie Freiberg, Gustav-Zeuner-Str. 5, D-09599 Freiberg, Germany

²Department of Condensed Matter Physics, Charles University Prague, Ke Karlovu 5, CZ-121 16 Prague 2, Czech Republic

Corresponding author: rafaja@ww.tu-freiberg.de (David Rafaja)

Keywords: Nanocomposites, partial coherence of crystallites, X-ray diffraction, line profile analysis, transmission electron microscopy

Abstract

The capability of the combination of the X-ray diffraction and the transmission electron microscopy for the microstructure investigations on thin film and bulk nanocomposites are illustrated on three experimental examples: two Cr-Al-Si-N coatings with different chemical compositions and one BN bulk nanocomposite. Using a modified kinematical diffraction theory that describes and explains the phenomenon of the partial crystallographic coherence of crystallites, we could show that the analysis of the X-ray diffraction line broadening is able to reveal nanocrystalline domains organised in semi-coherent clusters, to determine the size of the nanocrystalline domains and the clusters, and to quantify the mutual orientation of the partially coherent crystallites within these clusters.

Introduction

The knowledge of the microstructure of functional materials is inevitable for both explanation and modification of their properties. Thus, the microstructure analysis became an obligatory experimental method in the materials design in the last decades. One possibility for tailoring of the materials properties is the production of nanocrystalline materials or nanocomposites. Typical application fields of these materials are the catalytic converters, in which the extremely small size of the particles enlarges their active surface [1], the self-cleaning surfaces based on the TiO₂ thin films, in which the small crystallite size improves their photo-catalytic activity [2], or the magnetic materials, in which the magnetic behaviour can be modified by uncompensated magnetic moments in the near-surface region and thus by the ratio between the surface and the volume of crystallites [3, 4]. The experimental examples shown in this contribution illustrate the microstructure development in ultra-hard nanocomposites, in which the small crystallite size is employed to improve their mechanical properties, particularly their hardness [5]. The most important microstructure feature that improves the hardness in the ultra-hard nanocomposites is a high density of the crystallites boundaries, which hinder the movement of dislocations and some other microstructure defects. The increase of the hardness with decreasing crystallite size is described by the well-known Hall-Petch relationship [6, 7]. The optimum crystallite size in the ultra-hard nanocomposites is about 3 nm [8-10], which also agrees with the optimum thickness of individual layers in ultra-hard multilayers [11, 12]. If the crystallite size in the ultra-hard nanocomposites or the individual layer thickness in the ultra-hard multilayers are smaller than the optimum ones, their hardness decreases. In our Cr-Al-Si-N nanocomposite coatings, the maximum hardness reached 45 GPa. An additional experimental example illustrates the development of microstructure in bulk boron nitride nanocomposites, which hardness approached 100 GPa [13].

Concerning the role of the crystallite boundaries, it is anticipated that the mechanical properties of the ultra-hard nanocomposites are strongly influenced not only by their density, i.e. by the crystallite size, but also by their morphology and atomic structure. Therefore, besides the traditional tasks of the microstructure analysis, i.e. the phase analysis, the texture analysis, the analysis of the crystallite size, the analysis of the residual stresses and the micro-strains, also the analysis of the more subtle local microstructure features, like the atomic ordering at the crystallites boundaries, and the prediction of the intrinsic residual stresses are required. A very important approach for the local microstructure analysis using X-ray diffraction (XRD) is the line profile analysis and its modification that employs the phenomenon of the partial coherence of crystallites to the X-ray scattering [14]. The partial coherence of crystallites for X-rays is observed in nanocrystalline materials and in nanocomposites with the crystallite size below approximately 15 nm if adjacent crystallites are strongly preferentially oriented. The most important criterion for the maximum distance of the partially coherent crystallites is the coherence length of X-rays [15] that is, according to the Heisenberg’s uncertainty principle, related to the spectral quality of the radiation. More details regarding the coherence length of X-rays can be found in [16]. The maximum disorientation of the partially coherent neighbouring crystallites depends on their size, but it is usually below 2° [13, 17, 18]. Most frequently, the phenomenon of the partial coherence of crystallites is observed in nanocrystalline thin films [14, 17-20]. However, the partial coherence of crystallites was also reported for powders with a strong local preferred orientation of crystallites [21, 22]. The physical background of the partial coherence of crystallites was described in [14] and is summarised in the next Section. Some applications of the phenomenon of the partial coherence of crystallites for microstructure studies on nanocrystalline materials are illustrated by experimental examples in the experimental sections.

Phenomenon of the partial coherence of crystallites

The phenomenon of the partial coherence of crystallites can be explained using the microstructure model, which assumes that the material under study consists of nearly defect-free crystallites, which have slightly different macroscopic orientations (Fig. 1). Such a microstructure model is well applicable for impacted powders with a high local preferred orientation of crystallites, as well as for compact samples, which microstructure can be described with the aid of the Mughrabi composite model of plastic deformation [23]. According to the Mughrabi model, regions with very low dislocation density are separated by regions with a high dislocation density. The latter are called dislocation walls. If the defect density inside the dislocation walls is very high, it can be assumed that the dislocation walls do not contribute to the Bragg peaks diffracted by the defect-free crystallites. Thus, the contribution of the defect-free crystallites to the diffraction pattern can be separated from the contribution of the dislocation walls. A modification of the Mughrabi model can be applied for description of microstructure in nanocrystalline materials and nanocomposites that consist of nearly defect-free nanocrystallites and of strongly distorted regions between them.

Figure 1. Microstructure model used for description of the X-ray scattering in nanocrystalline materials. Nearly defect-free nanocrystallites are separated by regions with extremely high defect density.

Figure 2. Projection of the reciprocal lattices from two mutually disoriented fcc nanocrystallites into the q_x-q_z plane. The white circles belong to the first nanocrystallite, the grey circles to the second one. The numbers within the circles are the diffraction indices.

Each individual crystallite can be described by a single reciprocal lattice. According to the kinematical diffraction theory [24], the size of the reciprocal lattice points is inversely proportional to the size of the (nearly defect-free) crystallite that is known as the “size effect” in the XRD line profile analysis. The reciprocal lattice points from nanocrystallites are extremely broadened. The mutual disorientations of individual crystallites cause rotation of the reciprocal lattices around their join origin (Fig. 2). If the neighbouring crystallites have a strong local preferred orientation, then their reciprocal lattices are only slightly mutually disoriented that leads to a partial overlap of the reciprocal lattice points near the origin of the reciprocal space, as it is shown in Fig. 2 for two slightly disoriented crystallites with the face-centred cubic (fcc) crystal structure. The degree of the overlap of the reciprocal lattice points depends obviously on their size, on the mutual disorientation of the reciprocal lattices and on the distance of the respective reciprocal lattice points from the origin of the reciprocal space. In the kinematical diffraction theory, the intensity of the X-ray radiation scattered on an ensemble of the scattering centres is proportional to the modulus of the sum of the amplitudes scattered by individual scattering centres, i.e. to the modulus of the sum of the structure factors of the scattering centres, taking the respective phase shift into account:

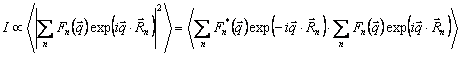, (1)

In equation (1), the symbol denotes the structure factors of the individual scattering centres, the diffraction vector and the position vectors of the scattering centres. In the theory of the partial coherence of crystallites, the “scattering centres” are replaced by “crystallites”; it is assumed that the X-rays scattered by different crystallites can interfere. The structure factor of nanocrystallites, i.e. in equation (1), is a very broad function because its width is reciprocal to the crystallite size. For identical (very similar) crystallites having the same structure factor, equation (1) can be rewritten into the following form:

(2)

Figure 3. “Narrowing” of a diffraction line due to the partial coherence of nanocrystallites. Thin solid line represents the structure factor of individual crystallites, the dotted line the harmonic function from equation (2) and the wide solid line their product.

Figure 4. Dependence of the XRD line broadening on the sinus of the diffraction angle calculated for partially coherent crystallites having the size of 80 Å. The size of the diffraction vector depends on the diffraction angle according to q = 4p sin q/l.

In equation (2), N is the number of diffracting crystallites and the degree of the partial coherence of crystallites with the distance . The degree of the partial coherence is proportional to the overlap of their reciprocal lattice points; w_m = 0 for non-coherent crystallites, w_m = 1 for fully coherent crystallites. In the classical kinematical diffraction theory, the interference term that is related to the partial coherence of crystallites, i.e. the sum in equation (2), is neglected. For overlapping reciprocal lattice points in nanocrystalline materials, the broad structure factor is multiplied by a harmonic function coming from the complex exponential function in equation (2), which frequency depends on the mean distance of the partially coherent crystallites. This multiplication causes a “narrowing” of the diffraction lines as shown in Fig. 3. The physical interpretation of this phenomenon is that the X-ray scattering cannot distinguish the crystallites with partially overlapping reciprocal lattice points from each other. Thus, the partially coherent nanocrystallites appear larger than they are.

According to equation (2), the amount of the “narrowing” of the diffraction lines depends on the mean distance of the partially coherent crystallites and on the degree of their coherence w_m. As discussed above (cf. also Fig. 2), the overlap of the reciprocal lattice points and thus the degree of the partial coherence of the related crystallites depend on the size of the reciprocal lattice points, i.e. on the crystallite size, on the mutual disorientation of the reciprocal lattices, i.e. on the mutual disorientation of neighbouring crystallites, and on the distance of the respective reciprocal lattice point from the origin of the reciprocal space, i.e. on the size of the diffraction vector. The dependence of the degree of the partial coherence on the size of the diffraction vector yields the dependence of the XRD line broadening on sin q that is shown in Fig. 4. For large diffraction vectors, there is no partial coherence of crystallites (see Fig. 2). The line broadening is only given by the width of the structure factor of the nanocrystallites. Thus, it remains constant in accordance with the classical diffraction theory, cf. Fig. 4. In Fig. 2, this case applies for the diffraction line 400 and farther. In the range of the diffraction vectors, where the crystallites are partially coherent, the diffraction lines get narrower that it would correspond to the reciprocal crystallite size. The decrease of the XRD line width is controlled by the degree of the partial coherence and by the mean distance between the partially coherent crystallites. As the degree of the partial coherence increases with decreasing size of the diffraction vector, the XRD lines become narrower towards the origin of the reciprocal space. At the onset of the partial coherence, a steep change of the line broadening is observed (Fig. 4). The position of the onset of the partial coherence is given by the mean disorientation of the partially coherent crystallites. The amount of the steep decrease of the XRD line broadening is mainly controlled by the mean distance of the partially coherent crystallites. The larger the distance between the crystallites, the higher the frequency of the oscillations of the harmonic function in equation (2) and the narrower the XRD lines. In analogy with the classical kinematical diffraction theory, we can assume that the extrapolation of the XRD line broadening to q = 0 yields the maximum size of clusters consisting of partially coherent crystallites that cannot be distinguished by the X-ray scattering. These clusters necessarily contain microstructure defects, which are, in this particular case, the small-angle crystallites boundaries as illustrated in Fig. 1.

Experimental details

Theoretical results summarised above were recently verified on numerous samples of nanocrystalline materials and nanocomposites that were investigated by the combination of the X-ray diffraction (XRD), transmission electron microscopy (TEM) and high resolution transmission electron microscopy (HRTEM). Two examples presented in this contribution illustrate the capability of these experimental methods for the microstructure studies on super-hard Cr-Al-Si-N thin film nanocomposites deposited using the cathodic arc evaporation. The details regarding the sample deposition can be found in [17] and [18]. An additional example shows the results of the microstructure studies on bulk super-hard BN nanocomposites that were produced during the high-pressure and high-temperature (HP/HT) synthesis at 15 GPa and 1660 °C [13]. The main tasks for the microstructure analysis in all these samples were to explain the development of nanocrystalline domains and to clarify the effect of the microstructure on the mechanical properties.

The XRD measurements on thin films were performed in the glancing angle XRD (GAXRD) geometry with the parallel beam optics. The experiments were carried out on a Bruker D8 diffractometer equipped by a Goebel mirror in the primary beam, and by a Soller collimator with the acceptance of 0.12° and a flat LiF monochromator located in the diffracted beam. The XRD measurements on bulk BN nanocomposites were done in the symmetrical diffraction geometry using the same Bruker D8 diffractometer, which was equipped by two Goebel mirrors; one of them was located in the primary beam, the second one in the front of a scintillation detector. The XRD was complemented by the high-resolution transmission electron microscopy (HRTEM) that was done on a 200 kV analytical high-resolution transmission electron microscope JEM 2010 FEF from Jeol equipped by ultra-high-resolution objective lens (C_s = 0.5 mm) and in-column energy filter. The in-column energy filter was used to select only the elastic electrons for the HRTEM image formation. Chemical composition of the samples was determined using the electron probe microanalysis with wavelength-dispersive spectroscopy of characteristic X-rays (EPMA/WDS).

Experimental results and discussion

According to the results of the EPMA/WDS analysis, the first Cr-Al-Si-N sample under study had the chemical composition of Cr_0.40Al_0.52Si_0.08N. At this chemical composition, the quaternary Cr_1-x-yAl_xSi_yN with the fcc crystal structure (space group F m3m, structure type NaCl) starts to decompose; the superfluous aluminium creates wurtzitic AlN (space group P 6₃mc, structure type ZnS) [18], the superfluous silicon an amorphous phase, probably Si₃N₄. In this particular sample, the broadening of the XRD lines from the cubic phase was independent of the size of the diffraction vector (Fig. 5), which means that the nanocrystallites were non-coherent in the whole accessible range of the diffraction vector. Thus, the XRD line broadening contains only the information about the mean size of the fcc crystallites, which was (50 ± 5) Å. As no steep increase of the line broadening, i.e., no effect of the partial coherence of crystallites was observed in the experimental data, we can only say that the smallest disorientation of the neighbouring crystallites exceeded 3°. HRTEM confirmed the crystallite size obtained from XRD, see Fig. 6. Moreover, HRTEM micrographs contained rotational moiré patterns [25], from which the minimum disorientation of the cubic crystallites of (7.8 ± 0.1) ° was calculated. The multi-phase microstructure of the sample and particularly the development of the amorphous phase are regarded as the reasons for the large mutual disorientations of cubic crystallites, because the presence of the amorphous phase hinders the transfer of the crystallographic orientation between individual crystallites [19].

Figure 5. XRD line broadening vs. sin q as observed for the sample Cr_0.40Al_0.52Si_0.08N. The solid line shows the XRD line broadening calculated for crystallite size of 50 Å and their mutual disorientation of 3°.

Figure 6. HRTEM micrograph of the sample Cr_0.40Al_0.52Si_0.08N showing mutually disoriented nanocrystallites.

An example of the partial coherence of crystallites in a multi-phase BN nanocomposite is illustrated in Figures 7 and 8. The sample was synthesized from hexagonal boron nitride (h-BN, space group P 6₃/mmc) at the pressure of 15 GPa and the temperature of 1660 °C. The h-BN crystallites in the starting material had the size of approximately 100 nm as revealed by the XRD line profile analysis. During the HP/HT synthesis, h-BN transforms via the meta-stable wurtzitic BN (w-BN, space group P 6₃mc) in the sphaleritic BN (c-BN, space group P -43m) by maintaining the following orientation relationships between the individual phases: (0002)_h || (0002)_w || (111)_c and [11`20]_h || [11`20]_w || [`110]_c, see [26, 27]. The XRD line profile analysis has shown that the phase transformation starts concurrently at different positions within the large h-BN crystallites in the starting material. The crystallite sizes in individual phases as calculated from the saturated XRD line broadening (Fig. 7) in the sample under study were (62 ± 3) Å for c-BN, (31 ± 2) Å for w-BN and (60 ± 3) Å for h-BN. With increasing temperature and for longer dwell times of the HP/HT conversion process, c-BN grew on the expenses of the other phases, i.e. h-BN and w-BN. After a long conversion time, the maximum size of the c-BN crystallites approached the size of the h-BN crystallites in the starting material [13]. An example of the microstructure of the BN nanocomposites during the HP/HT conversion is shown in Fig. 8a, where structured particles coming from the crystallites of the starting h-BN with the size of » 100 nm can be recognised. These particles contain c-BN, w-BN and h-BN as revealed by XRD.


Figure 7. XRD line broadening vs. sin q measured in the c-BN (a), w-BN (b) and h-BN (c) phases of a BN nanocomposite.		Figure 8. (a) Bright-field TEM micrograph of the BN nanocomposite; (b) HRTEM micrograph of the microstructure defects in h-BN.

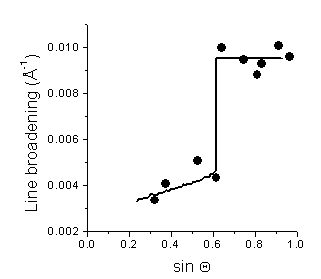
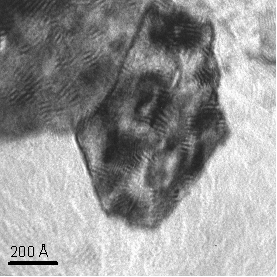
Figure 9. XRD line broadening vs. sin q as measured for the sample Cr_0.91Al_0.08Si_0.01N.	Figure 10. Bright-field TEM micrograph of the sample Cr_0.91Al_0.08Si_0.01N showing clusters of nanocrystallites

The steep increase of the XRD line broadening in Fig. 7 at sin q @ 0.4 indicates the partial coherence of crystallites in the c-BN and w-BN phases. The mutual disorientation of the partially coherent c-BN crystallites is (1.02 ± 0.04) °, the mutual disorientation of the partially coherent w-BN crystallites (1.01 ± 0.05) °; both were calculated from the position of the steep increase of the XRD line broadening. Because of the non-coherence of the h-BN crystallites within the accessible range of the diffraction angles, their mutual disorientation could only be estimated to be larger than 1.4°.

The partial coherence of crystallites having the respective crystal structure, i.e. c-BN or w-BN, is made possible by their strong local preferred orientation, which results from the preservation of the orientation relationships between the h-BN, w-BN and c-BN phases during the HP/HT transformation process [26, 27]. Vice versa, the effect of the partial coherence confirmed that the c-BN and w-BN crystallites did not change significantly their disorientation during the transformation process. The large disorientation of the h-BN crystallites that led to the disappearance of their partial coherence was explained by HRTEM. HRTEM discovered remnants of h-BN predominantly between c-BN crystallites. These remnants of h-BN, which looked like twinning bands (Fig. 8b), were found to contain an extremely high number of structure defects at their boundaries. These defects caused the high mutual disorientation of the h-BN crystallites that destroyed the partial coherence in this phase. We believe that such remnants of h-BN persist in the nanocomposite as they are resistant against the phase transformation. The energy accumulated in their internal structure defects is probably too high to be overpowered by the mechanical and thermal energy available at the pressures and the temperatures that were applied during the HP/HT synthesis.

The last experimental example illustrates the partial coherence of crystallites in a super-hard coating with the chemical composition Cr_0.91Al_0.08Si_0.01N. This sample contained only one fcc phase as Al and Si in low concentrations can be accommodated in the host structure of the fcc CrN. The dependence of the XRD line broadening on the sinus of the diffraction angle (Fig. 9) confirms the theoretical results that were summarised in Fig. 4. The crystallite size as calculated from the saturated XRD line broadening was (140 ± 5) Å. The steep decrease of the line broadening at sin q @ 0.6 indicates the presence of the partial coherence of crystallites. From the position of this increase, the disorientation of the partially coherent crystallites of (0.6 ± 0.1) ° was calculated. As discussed above, the extrapolation of the XRD line broadening in the partially coherent region to sin q = 0 (q = 0) should reveal the size of clusters, which are composed from partially coherent crystallites that cannot be distinguished from each other. The extrapolation of the line broadening in the range of the partial coherence of crystallites, i.e. the first four experimental values in Fig. 9, yielded the cluster size of (400 ± 200) Å. The comparison with the TEM micrograph (Fig. 10) confirmed the results of XRD and explained the meaning of the individual microstructural features. The large objects in Fig. 10 are the clusters of partially coherent crystallites that are composed from nanocrystallites with the mean size of 140 Å and with the mutual disorientation of 0.6°.

As illustrated on the first two examples, the small crystallite size is often related to the multi-phase nature of the samples. In the thin film nanocomposites, several phases arise during the decomposition of the material during the deposition process. In the BN nanocomposites, the individual phases develop during the HP/HT synthesis as different parts of the original h-BN crystallites transform with different rate. The last example illustrated the development of partially coherent nanocrystallites in the single-phase Cr_0.91Al_0.08Si_0.01N coating. In this sample, TEM revealed dislocation walls, which behaved like complete screw dislocations with the Burgers vector a/2á110ñ and which had the average distance of ~22 nm [18]. According to [28], these screw dislocations cause a disorientation of the neighbouring crystallites of ~0.75°, which agrees well with the mutual disorientation of crystallites obtained from the XRD line profile analysis. It seems that in this sample the dislocation walls separate the nearly defect-free nanocrystallites from each other. As the crystallite size obtained from XRD was 14 nm whereas the distance between the dislocation walls was 22 nm, we can suppose that XRD sees only the nearly defect-free nanocrystallites, but not the dislocation walls.

Conclusions

Combination of XRD, TEM and HRTEM on nanocrystalline thin films and different nanocomposites confirmed our theoretical results that were obtained using the modified kinematical XRD theory derived for partially coherent nanocrystallites. According to this theory, the XRD line broadening behaves differently for non-coherent and for partially coherent nanocrystallites. Furthermore, the degree of the partial coherence of crystallites depends on their size, on their disorientation and on the size of the diffraction vector. At large diffraction vectors, the nanocrystallites are usually non-coherent. The line broadening does not change with the size of the diffraction vector; it depends only on the crystallite size. In the middle range of the diffraction vectors, onset of the partial coherence is observed if the nanocrystallites have a strong local preferred orientation. The partial coherence of crystallites causes a decrease of the line broadening with decreasing size of the diffraction vector. From the position of the onset of the partial coherence, the mutual disorientation of the partially coherent nanocrystallites can be determined. The extrapolation of the XRD line broadening to q = 0 yields the size of clusters of partially coherent crystallites.

References

1. C. Roth, N. Martz, H. Fuess, Phys. Chem. Chem. Phys., 3, (2001), 315.

2. Z.B. Zhang, C.C. Wang, R. Zakaria, J.Y. Ying, J. Phys. Chem. B, 102, (1998), 10871.

3. D. Rafaja, L. Havela, R. Kužel, F. Wastin, E. Colineau, T. Gouder, J. Alloys Comp., 386, (2005), 87.

4. L. Havela, K. Miliyanchuk, D. Rafaja, T. Gouder, F. Wastin, J. Alloys Comp., 408-412, (2006), 1320.

5. S. Vepřek, S. Reiprich, Thin Solid Films, 268, (1995), 64.

6. E.O. Hall, Proc. Phys. Soc. London Sect. B, 64, (1951), 747.

7. N. J. Petch, J. Iron Steel Inst., 174, (1953), 25.

8. A. Niederhofer, P. Nesládek, H.-D. Männling, K. Moto, S. Vepřek, M. Jílek, Surf. Coat. Technol., 120–121, (1999), 173.

9. S. Vepřek, J. Vac. Sci. Technol., A 17, (1999), 2401.

10. S. Vepřek, A. Niederhofer, K. Moto, T. Bolom, H.-D. Männling, P. Nesládek, G. Dollinger, A. Bergmaier, Surf. Coat. Technol., 133-134, (2000), 152.

11. C.J. Tavares, L. Rebouta, E. Ribeiro, J.P. Riviere, J. Pacaud, M.F. Denanot, Surf. Coat. Technol., 174-175, (2003), 273.

12. S.Y. Lee, G.S. Kim, J.H. Hahn, Surf. Coat. Technol., 177-178, (2004), 426.

13. M. R. Schwarz, T. Barsukova, E. Kroke, M. Motylenko, V. Klemm, D. Rafaja, D. Frost, L. Dubrovinsky, N. Dubrovinskaia, J. Mater. Res., (2007), submitted.

14. D. Rafaja, V. Klemm, G. Schreiber, M. Knapp, R. Kužel, J. Appl. Cryst., 37, (2004), 613.

15. M. Born & E. Wolf, Principles of optics – electromagnetic theory of propagation, interference and diffraction of light. 7^th edition. Cambridge: Cambridge University Press. 1999.

16. U. Pietsch, V. Holý, T. Baumbach, High-resolution X-ray scattering – from thin films to lateral nanostructures. 2^nd edition, New York: Springer. 2004.

17. D. Rafaja, M. Dopita, M. Růžička, V. Klemm, D. Heger, G. Schreiber, M. Šíma, Surf. Coat. Technol., 201, (2006), 2835.

18. D. Rafaja, C. Wüstefeld, M. Dopita, M. Růžička, V. Klemm, G. Schreiber, D. Heger, M. Šíma, Surf. Coat. Technol., (2007), doi: 10.1016/j.surfcoat.2007.04.007.

19. D. Rafaja, A. Poklad, V. Klemm, G. Schreiber, D. Heger, M. Šíma, M. Dopita, Thin Solid Films, 514, (2006), 240.

20. D. Comedi, O.H.Y. Zalloum, E.A. Irving, J. Wojcik, T. Roschuk, M.J. Flynn, P. Mascher, J. Appl. Phys., 99, (2006), art. no. 023518.

21. G. Ribárik, N. Audebrand, H. Palancher, T. Ungár, D. Louër, J. Appl. Cryst., 38, (2005), 912.

22. T.K. Mandal, Mater. Letters, 61, (2007), 850.

23. H. Mughrabi, Acta Metall., 31, (1983), 1367.

24. See, e.g., C. Giacovazzo, H.L. Monaco, G. Artioli, D. Viterbo, G. Feraris, G. Gilli, G. Zanotti, M. Catti, Fundamentals of Crystallography, 2^nd Edition, IUCr Texts on Crystallography 7, Oxford: University Press. 2002.

25. D.B. Williams & C.B. Carter: Transmission Electron Microscopy III – Imaging, New York: Plenum Press. 1996.

26. A.V. Kurdyumov, V.F. Britun, I.A. Petrusha, Diam. Relat. Mater., 5, (1996), 1229.

27. J. Huang, Y.T. Zhu, Defect Diffus. Forum, 186-187, (2000), 1.

28. F.C. Frank: Report on the Symposium on Plastic Deformation of Crystalline Solids, Carnegie Institute of Technology and Office of Naval Research, Washington: U.S. Government Printing Office. 1950.

Acknowledgements.

The authors would like to thank to the German Research Council (DFG) for supporting the project # RA-1050/9. HRTEM Jeol 2010 FEF was purchased from the funds of the DFG Priority Programme # 1062. The support of the project # RA-1050/7 within the Priority Programme # 1181 "Nanoskalige anorganische Materialien durch molekulares Design" through DFG is also gratefully acknowledged. Furthermore, we would like to thank Dr. M. Růžička and Dr. M. Šíma from the SHM Šumperk Ltd. for deposition of the Cr-Al-Si-N coatings by means of the cathodic arc evaporation and Dr. M. Schwarz and Mrs. T. Barsukova from the Institute of Inorganic Chemistry of the TU Bergakademie Freiberg for the HT/HP synthesis of the BN nanocomposites.