Evolution of the spontaneous lateral
composition modulation in InAs/AlAs superlattices on InP
O. Caha1,
V. Holý1,2, K. E. Bassler3
1Institute of condensed matter
physics, Masaryk University, Brno,
2Department of electronic structure,
Charles University, Praha,
3Department of physics, University of
Houston, Houston,
caha@physics.muni.cz
During
growth of short-period superlattices, spontaneous lateral composition
modulation can occur leading to a quasiperiodic modulation of the thicknesses
of individual layers; resulting one-dimensional nanostructures (quantum wires)
have potential applications in optoelectronics [1]. Theoretical description of
the modulation process is based on two different models. If there is a high density
of monolayer steps on the vicinal surface (the crystallographic miscut angle is
larger than approx. 1o), a step-bunching instability occurs [2], but
if the density of the the monolayer steps is low, a self-organized growth of
two-dimensional or three-dimensional islands takes place. The latter process
occurs, if the reduction of the strain energy due to an elastic relaxation of
internal stresses in the islands outweighs the corresponding increase of the
surface energy (morphological Asaro-Tiller-Grinfeld (ATG) instability [3]).
The dependence of the lateral composition modulation
on the number of layers was investigated using grazing incidence x-ray
diffraction. The serie of four samples of InAs/AlAs superlattices grown by
molecular beam epitaxy (MBE) on an InP(001) substrate was studied; the
substrate was prepared without any nominal miscut. The samples have 2, 5, 10
and 20 superlattice periods; the InAs and AlAs thicknesses were nominally 1.9
monolayers in all samples. For all
samples, we have measured the intensity distribution of the grazing-incidence
400 and 040 diffraction in the qxqy plane of the
reciprocal space, i.e. parallel to the sample surface. The x-ray measurements
have been carried out at the beamline ID01 of the European Synchrotron Radiation
Facility (ESRF,
From the experiment follows that the modulation
amplitude increases with the number of layers, the lateral modulation period <L>=(267
± 15) Å remains constant during the growth, while the
width of the lateral satellites decreases with N as N-0.2
[4].
From this behavior it follows that the first stages of
the spontaneous modulation of the average chemical composition of a
short-period superlattice cannot be explained as a result of the bunching of
monolayer steps at the interfaces. Most likely, this behavior can be ascribed
to the ATG instability, in which the critical wavelength of the surface
corrugation, Lcrit depends on the stress in the growing
layer, elastic constants and its surface energy. The evolution of the surface morphology
of multilayers has been studied only in a linearized approach so far [5]. From
this approach, an unlimited growth of the modulation amplitude follows, which
does not correspond to the experimentally observed stabilization of the
modulation amplitude during the growth.
We have simulated a full nonlinear time evolution
equation of the spontaneous lateral modulation and we have obtained the
critical wavelength Lcrit=300 Å. The particular values of diffusion rate have
only weak influence on the resulting interface morphology. We have also found
that the nonlinear dependence of the strain energy on the layer thickness
(wetting effect) has a crucial influence on the resulting interface morphology.
The parameters of this nonlinear dependence were determined from the fit of the
experimental data with the simulation and these values were compared with the
atomistic calculation [6]. The resulting experimental and theoretical
dependence of the modulation amplitude on the number of superlattice periods is
plotted in Fig. 1.
1.
A. G. Norman, S. P. Ahrenkiel, C. Ballif, H. R.
Moutinho, M. M. Al-Jassim, A. Mascarenhas, D. M. Follstaedt, S. R. Lee, J. L.
Reno, E. D. Jones, R. D. Twesten, and J. Mirecki-Millunchick, Mater. Res. Soc.
Symp. Proc. 583, 297 (2000).
2.
L. Bai, J. Tersoff, and F. Liu, Phys. Rev. Lett. 92, 225503 (2004).
3.
R. J. Asaro and W. A. Tiller, Metall. Trans. 3,
1789 (1972); M. A. Grinfeld, Sov. Phys. Dokl. 31, 831 (1986).
4.
O.
Caha, P. Mikulík, J. Novák, V. Holý, S. C. Moss, A. Norman, A. Mascrenhas, J.
L. Reno, and B. Krause, Phys. Rev. B 72,
035313 (2005).
5.
Z.-F.
Huang, R. C. Desai, Phys. Rev. B 67, 075416 (2003).
6. O.
Caha, V. Holý, and K. E. Bassler, Phys. Rev. Lett. 96, 136102 (2006).
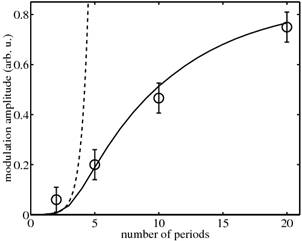
Figure 1. The dependence of the modulation amplitude on the number of superlattice periods. The circles with error bars are the experimental points obtained from the x-ray data, the full line represents the simulations. The dashed line is the evolution of the modulation amplitude calculated in the linearized approach [5].