NANO-MECHANICAL PROPERTIES OF CARBON AND SILICON FILMS

M. Stranyánek¹, R. Čtvrtlík¹, P. Boháč¹, L. Jastrabík¹

¹Institute of Physics, Academy of Sciences of the Czech Republic, Na Slovance 2, 182 21 Praha 8, Czech Republic.

Keywords

nanoindentation, NanoTest^TM, thin films

Abstract

The depth sensing indentation technique is increasingly being used to probe the mechanical properties of materials. There is referenced the Oliver-Pharr method for analyzing indentation load-depth data in this paper. We determined the hardness and the elastic modulus of thin films prepared by magnetron sputtering experimentally using The NanoTest^TM instrument. Load was applied by force in horizontal direction. This untraditional arrangement of the experiment allows just original construction of the NanoTest platform.

1. Introduction

The chemical resistant and the high hardness of diamond-like carbon films allow some tribology applications. Amorphous carbon films commonly have resistance against abrasive and adhesive wear and the low coefficient of friction. Special thin films can enlarge the operating lifetime of product. Research and development of new and superior procedures of the surface treatment of material can bring significant increase of product manufacture qualities moreover savings of the critical materials. An Investigation of mechanical properties allows produce layers and coatings with exactly defined features.

The Instrumented indentation offers advances in sensitivity and data acquisition. These benefits are significant in materials science particularly regarding fundamental mechanisms of mechanical behaviour at micrometer and even sub-micrometer length scales.

We examined a-C a a-C:Si films from amorphous carbon on Si substrates. The thin films produced by the DC magnetron sputtering from carbon target in chemically poor argon in vacuum chamber (with the stuck Si little sheet in the second case) of commercial vacuum machinery the Leybold Z 550M. A description of the sputtering equipment and deposition parameters were published previously e.g. [1]. Thickness of the layers was measured by the ALPHA STEP 500 apparatus. Sample a-C no. 516: 1,62 mm, sample a-C:Si no. 846-1: 2,29 mm. We measured certain silicon films as well. Its indentation behaviour is more complicated by cracking and pressure-induced phase transformation [2, 3].

2. Instrumented indentation

Depth sensing indentation (DSI) also known as instrumented indentation or nanoindentation [4] is increasing being used to evaluate the mechanical properties of materials having very fine microstructure such as thin films. In contrast to traditional hardness testers instrumented indentation systems allow the application of a specified force or displacement course. The force and the displacement are controlled and measured simultaneously and continuously over a complete loading cycle. Moreover the extremely small force and displacement resolutions often < 1 mm are possible.

Fig. 1. Indentation part of the NanoTest^TM system: 1 – indenter, 2 – samples, 3 – pendulum, 4 – capacitor plates, 5 – sample holder with x-y-z nano-feedings, 6 – microscope.

Many instrumented indentation systems can be found on the market. We used commercial the NanoTest^TM NT600 platform. The instrument makes use of its unique pendulum design (Fig. 1). The pendulum pivoted on frictionless bearings combines vibrating stability with the ability to carry out a wide range of measurements. To measure nano-mechanical properties a very small calibrated diamond indenter is brought into contact with the sample surface and a load is applied by means of a coil and magnet located at the top of the pendulum. The resultant displacement of the probe into the surface is monitored with a sensitive capacitive transducer in real time as a function of load [5].

After reaching a predefined maximum value the load is reduced and the penetration depth decreases due to the elastic recovery of the deformed material. The depth and load are monitored continuously which allows both hardness and elastic modulus to be determined.

3. Analysis of the nanoindentation data

Different analytical approaches were developed to extract mechanical properties, generally the hardness H and the elastic modulus E. The Oliver-Pharr method introduced in 1992 [6] and refined in 2004 [7] comes from former publications such as [8]. This principle is used in the characterization of mechanical behavior of materials at small scales. By this techniques a mechanical properties can be determined directly from indentation load and displacement measurements without the need to image the hardness impress. For this reason, the method has become a primary technique for determining the nano-mechanical properties of thin films and small structural features.

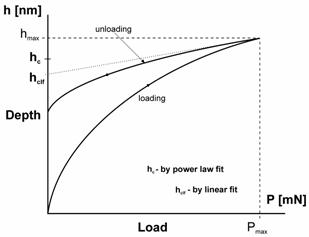
Fig. 2. One cycle of load-displacement data and contact depth determination.

In principle the method was developed to measure the hardness and elastic modulus of material from indentation load-displacement data obtained during one cycle of loading and unloading (Fig. 2). Parameter P is the load and h the displacement relative to the initial non-deformed surface. The method is essentially an extension of the method proposed by Doerner and Nix [8] (linear fitting – Fig. 2). Experiments have shown that unloading curves are distinctly curved and P-h raw data are usually well approximated by the power law relation (1). Where a , h_f and m are constants.

(1)

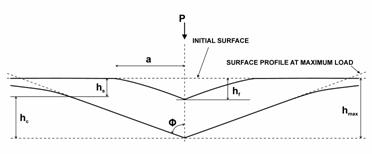
Fig. 3. Schematic illustration of the unloading process [6, 7].

There are three important quantities that must be measured from the curves. The maximum load P_max, the maximum displacement h_max and S the elastic unloading stiffness [7] (contact stiffness [9]) defined (3) as the slope of the upper portion of the unloading curve during the initial stages of unloading. Another important quantity is the final depth h_f the permanent depth of penetration after the indenter is fully unloaded. The accuracy of hardness and modulus measurement depends on how well these parameters can be measured experimentally.

There are a cross section of an indentation and the analysis parameters in Fig. 3. Total displacement is written as (2). Distance h_s is the displacement of the surface at the contact perimeter.

(2)

The contact depth h_c (likewise called plastic depth [8]) is the depth of indenter in contact with the sample under maximal load (4). The geometric constant for the Berkovich indenter e = 0,75. This value comes from modelling [6] by a paraboloid geometry.

(3)

(4)

The area of contact is determined by the geometry of the indenter and the depth of contact by area function (5) which relates the cross-sectional area of the indenter to the distance from its tip. This function must be established experimentally prior to analysis. For a perfect Berkovich indenter the A_c = 24,5·h_c². A real indenter is never perfect due to some tip rounding. The function may be determined for an example as (6) type where L and K are constants.

(5)

(6)

Measurements of the initial unloading slope can be used to determine the reduced modulus E_r. The reduced modulus is related to the contact area and measured stiffness by (7).

(7)

(8)

The equation (8) takes account effects of non-rigid indenters on the load-displacement behaviour. E_i and n_i are Young´s modulus and Poisson´s ratio for the indenter (diamond) which can be taken as 1 141 GPa and 0,07 respectively [5], E and n are properties of the sample.

The data obtained using the Oliver-Pharr method can be used to determine the indentation hardness defined by equation (9).

(9)

4. Experiment

We measured both carbon samples stuck on the one dural sample holder by quick drying cyanoacrylate industrial superglue Permabond. The silicon films we affixed by a wax on another dural holder. The melting temperature of the wax is approximately 60°C.

The experiment we programmed in the control NanoTest software. The indents we arranged to a matrix (Fig. 4). The matrix consisted from several single indents in one column measured at one maximum load with the indentation offset 30 mm. The dimension of the matrix in horizontal axis is given by number of experiments at one maximum load. There is possible up to 100 indentation experiments each containing up to 100 indentations to be scheduled in the NanoTest control software [5].

Fig. 4. The matrix of indents defined in the NanoTest software.

The experiment was controlled by electronic control unit and the computer. Before the auto-run we left the instrument and prepared samples at the constant temperature 26°C during 6 hours.

5. Results

Determined dependencies of hardness and reduced elastic modulus versus maximum load on measured carbon films are in the following figures. Some measurement results on silicon film are shown too.

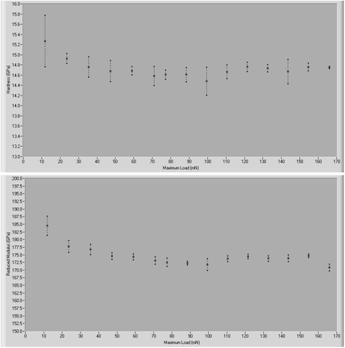
Fig. 5. Hardness and reduced modulus vs. maximum load on carbon film (sample no. 516).

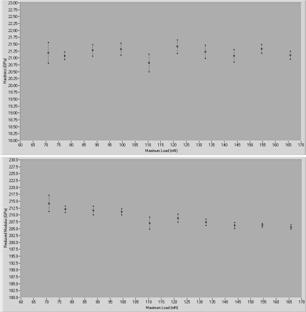
Fig. 6. Hardness and reduced modulus vs. maximum load on carbon film (sample no. 846-1).

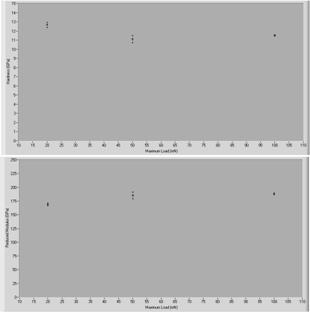
Fig. 7. Hardness and reduced modulus vs. maximum load on silicon film (sample no. 941).

Acknowledgements

This work was supported by Institutional Research Plan No. AV0Z10100522.

References

1. V. Kulikovsky, P. Bohac, F. Franc, A. Deineka, V. Vorlicek, L. Jastrabik, Hardness, intrinsic stress, and structure of the a-C and a-C:H films prepared by magnetron sputtering. Diamond and Related Materials, 10 (2001) 1076–1081.

2. G.M. Pharr, W.C. Oliver & D.R. Clarke, Hysteresis and discontinuity in the indentation load-displacement behavior of silicon. Scripta Metallurgica, 23 (1989) 1949–1952.

3. G.M. Pharr, W.C. Oliver & D.S. Harding, New evidence for a pressure-induced phase transformation during the indentation of silicon. Journal of Materials Research, 6 (1991) 1129–1130.

4. M.R. VanLandingham, Review of Instrumented Indentation. Journal of Research of the National Institute of Standards and Technology, 108 (2003) 249–265.

5. B. Beake, S. Goodes et al : Micro Materials NanoTest User Manual Version 2.0. Wrexham 2003. Micro Materials Ltd.

6. W.C. Oliver, G.M. Pharr, An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. Journal of Materials Research, 7 (1992) 1564–1583.

7. W.C. Oliver, G.M. Pharr, Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. Journal of Materials Research, 19 (2004) 3–20.

8. M.F. Doerner, W.D. Nix, A method for interpreting the data from depth-sensing indentation instruments. Journal of Materials Research, 1 (1986) 601–609.

9. J. Gong, H. Miao & H. Peng, Analysis of the nanoindentation data measured with a Berkovich indenter for brittle materials: effect of the residual contact stress. Acta Materialia, 52 (2004) 785–793.