ANALÝZA DIFRAKČNÍCH PROFILŮ ZLATÝCH NANOČÁSTIC

Zdeněk Matěj ¹, Radomír Kužel ¹ a Miroslav Šlouf ²

¹ Katedra fyziky elektronových struktur, Matematicko-fyzikální fakulta, Univerzita Karlova v Praze, 121 16 Praha 2, Ke Karlovu 5

² Ústav makromolekulární chemie, Akademie věd České Republiky, Heyrovského nám. 2, 162 06 Praha 6

Rentgenovou práškovou difrakcí byly studovány velmi malé částice zlata připravené chemickou reakcí ve formě koloidních roztoků, které byly pro difrakční měření naneseny v tenkých vrstvách na skleněné podložky [1]. Částice byly připraveny se záměrem je využít jako kalibrační částice pro měření dynamického rozptylu světla, byly zkoumány i dalšími metodami (TEM, UV/vis) a byla známa jejich velikost a tvar [1-2].

Malé množství materiálu v tenkých vrstvách vyžaduje použití geometrie paralelního svazku s malým úhlem dopadu. Popis fyzikálního rozšíření difrakčních profilů je v této geometrii stejný jako v případě klasického Braggova-Brentanova symetrického uspořádání, nevýhodou je ale velké vlastní přístrojové rozšíření difrakcí (FWHM=0.27°) a nelineární pozadí způsobené rozptylem na skleněné podložce, které ovšem bylo proměřeno a odečteno od difrakčních záznamů.

Naměřené profily jednotlivých linií difrakčního záznamu byly fitovány analytickými funkcemi a z jejich parametrů (po odečtení přístrojového rozšíření metodami numerické dekonvoluce) byly určeny profilové parametry difrakcí (FWHM, integrální šířka, Lorentzovská/Gaussovská povaha píku). Zkoumáním těchto parametrů (známá metoda Williamsonova-Hallova grafu) lze určit velikost krystalitů, povahu a množství poruch v krystalu [3-5]. Pomocí programu PM2000 byly modelovány celé difrakční záznamy (metoda WPPM) [6-7].

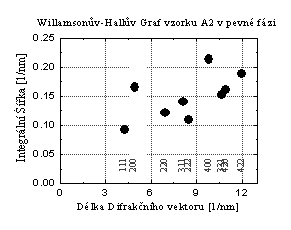
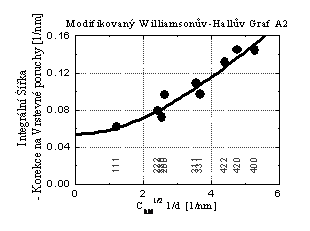
Malá velikost krystalitů se projevuje rozšířením píků, které nezávisí na velikosti difrakčního vektoru (sin Q) a šířka linií v reciprokých jednotkách (1/Å) je (v případě kulových zrn) pro všechny difrakce (hkl) stejná. Z obrázku 1 je ale naopak zřejmá velká anizotropie rozšíření profilů a zvětšování šířky píků s délkou difrakčního vektoru. Takové chování je příznačné pro rozptyl na deformačním poli poruch krystalové mříže (anizotropní kontrast dislokací - podobně jako např. v TEM a vrstevných poruch) [3-5,8-10]. Některé poruchy (vrstevné chyby) navíc způsobují asymetrii a posun píků [3-5,10]. Anizotropní rozšíření profilů v nanokrystalických materiálech připravených z roztoku, které se podařilo vysvětlit přítomností dislokací, už bylo pozorováno např. v [8]. Až uvážením vlivu dislokací (obrázek 2: metoda modifikovaného WH grafu - x-ová osa přenásobena orientačními kontrastními koeficienty, které byly spočítány pomocí programu ANIZC[9]) a vrstevných poruch bylo možné chování rozšíření profilů vysvětlit. Zahrnutím těchto defektů při modelování profilů (WPPM) [6-7,10] bylo dosaženo výrazně lepší shody výpočtu a naměřených dat (obrázek 3).

Obrázek 1. Williamsonův-Hallův Graf vzorku A2 (Dteor = 11  nm)	Obrázek 2. Modifikovaný Williamsonův-Hallův Graf [8] vzorku A2 (Dteor = 11 nm). Rozšíření píků způsobené vrstevnými poruchami bylo odečteno od integrálních šířek.

Obrázek 3. Modelování celého difrakčního záznamu vzorku A2 (D_teor = 11 nm) programem PM2000 [6-7].

Důležité výsledky profilové analýzy 4 vzorků s různou velikostí částic jsou uvedeny v tabulce 1. Velikost krystalitů určená rtg. práškovou difrakční analýzou je v dobré shodě s velikostí částic určených jinými metodami. Málá difraktovaná intenzita ale zapříčiňuje velkou nepřesnost určení velikosti krystalitů zvolenými metodami profilové analýzy, protože jednotlivé profily není možné naměřit dostatečně přesně, aby se daly zcela oddělit různé příčiny rozšíření píků a určit jednoznačně rozdělení velikosti krystalitů. Překvapivá je přítomnost velké mikrodeformace uvnitř krystalitů (velká hustota dislokací - asi 6x10¹⁵ m^-2) a výskyt růstových vrstevných poruch (až 8% ve vzorku s nejmenšími částicemi).

	dtheor (nm)	ddiff (nm)	rdiff (10^15 m^-2)	btwin
Au1	4.5	10±6	5±2	0.08±0.03
Au2	11.1	15±5	6±1	0.07±0.02
Au3	33.4	31±5	6.6±0.5	0.05±0.01
Au4	101.5	92±20	9±2	0.012±0.005

Tabulka 1: Teoretická velikost zrn (d_theor), velikos krystalitů určená z rozšíření profilů (d_diff), hustota dislokací (r_diff) a pravděpodobnost výskytu růstových vrstevných chyb (b_twin) určené z rtg. difrakčních profilů.

[1] M. Šlouf, R. Kužel, Z. Matěj, Materials Structure, 11 (2004) 166-168.

[2] M. Šlouf, přednáška na tomto kolkviu.

[3] B. E. Warren: X-ray diffraction. 1969. Addison-Wesley.

[4] V. Valvoda a kolektiv: Základy strukturní analýzy. Praha 1992. Karolinum.

[5] M. A. Krivoglaz: X-ray and Neutron Diffraction in Nonideal Crystals. Berlin 1996. Springer-Verlag.

[6] P. Scardi, M. Leoni, Acta Cryst. A, 58 (2002) 190-200.

[7] P. Scardi, M. Leoni, Y. H. Dong, Eur. Phys. J. B, 18 (2000) 23-30.

[8] T. Ungár, I. Dragomir-Cernatescu, D. Louer, N. Audebrand, J. Phys. Chem. Sol., 62 (2001) 1935-1941.

[9] A. Borbély, J. Dragomir-Cernatescu, G. Ribárik, T. Ungár, J. Appl. Cryst., 36 (2003) 160-162.

[10] P. Scardi, M. Leoni, R. Delhez, J. Appl. Cryst., 37 (2004) 381-390.