X-ray diffraction from polycrystalline multilayers with flat interfaces in grazing-incidence geometry

P. F. Fewster, N. L. Andrew

PANalytical Research Centre, Sussex Innovation Centre, Falmer, Brighton, UK

V. Holý

Department of Physics of Electronic Structures, Charles University, Prague, Czech Republic

K. Barmak

Department of Materials Science and Engineering, Carnegie Mellon University, Pittsburgh, U.S.A.

J. Krčmář

Institute of Condensed Matter Physics, Masaryk University, Brno, Czech Republic

I. INTRODUCTION

X-ray powder difractometry is a standard method for obtaining the size of crystallites in industrial materials. However in general the method is suited to obtaining the size normal to the surface using the focusing Bragg-Brentano geometry. To estimate the general shape of crystallites in bulk samples, several reflections are required, however this method is less suited to thin films that in general exhibit significant texture. Hence these methods are essentially bulk methods, i.e. they assume a random distribution of orientations and become difficult in the analysis of thin films when the crystallite size in the plane of the interface cannot be determined. Access to scattering planes normal to the interface is possible at grazing angles of incidence. This in-plane scattering geometry relies on the refractive index of X-rays being less than unity, such that there is a critical angle for total external refection. Thus the X-rays can enter through the sample surface, scatter from planes normal to the surface plane and then scatter out through the same surface. By varying the angle of incidence the penetration depth is varied. This has been used extensively in the study of mono-crystalline semiconductor wafer samples and can also be shown to work for very thin (30nm) polycrystalline layers. Although some average crystallite size is determined, knowledge of the variation as a function of depth in thin films can be very valuable.

This paper describes a new method to measure the crystallite size and its distribution as a function of depth in multi-layer thin films. The principle relies on the idea that when X-rays are scattered at an interface the incident and scattered waves create a standing wave whose periodicity can be varied and thereby enhance the scattering at certain depths.

II. THEORETICAL DESCRIPTION

In the in-plane grazing-incidence geometry, both the angle of incidence α_i of the incident radiation, and the angle of exit α_f of the scattered beams are comparable with the critical angle α_c of total external reflection of x-rays (Fig. 1). Thus, the interaction of x-rays with matter is rather strong and it cannot be described by a simple kinematical approximation. On the other hand, the polycrystalline grains can be assumed much smaller than the extinction length τ of x-rays in the material, so that the individual grains scatter kinematically.

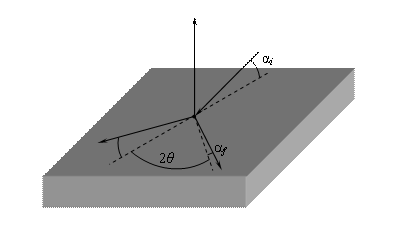
Fig. 1: Grazing incidence diffraction, the crystallographic plane is perpendicular to crystal surface.

We describe the scattering process using the distorted-wave Born approximation (DWBA) [1], in which the total scattering potential occurring in the wave equation:

(1)

is divided in two terms The first term describes the undisturbed system, the latter is the disturbance. Within the DWBA, the undisturbed wave equation with is solved exactly, while the scattering from is assumed kinematical.

In simple model with flat interfaces corresponds to an amorphous multi-layer and we assume that the primary x-ray beam E_i is scattered by which generates a standing wave-filed in the multi-layer; this wave-field is diffracted in the polycrystalline grains due to . The diffracted wave-field, is scattered again by and finally, the measured wave-field E_f results. In this choice, we completely neglect the scattering from interface roughness.

We assume a sample consisting in N layers. The wave-field in layer j is generated by the incident wave E_i consists of transmitted and reflected components and their amplitudes can be calculated using the well-known matrix formalism [2]. The second, independent solution of Eq. (1) (where) is chosen so that its vacuum incident wave equals the actual scattered wave E_f and this solution is time inverted.

The diffuse part of differential cross-section of the diffraction from polycrystalline grains is [1]:

, (2)

where denotes the averaging over a statistical ensemble of random positions R_jn (position vector of grain n in layer j), of the grains, random directions of h_jn (reciprocal lattice vector of grain), and over random grain sizes. The matrix elements υ_B is:

, (3)

and disturbance comprises the crystal structure of individual polycrystalline grains

III. NUMERICAL EXAMPLES

In the simulations, we have assumed the multi-layer consists of 14 periods, each contains a 4 nm thick Nb layer and a 11 nm thick Al layer. We also assume that the polycrystalline grains are spherical, each grain has the same radius R, grain positions are completely uncorrelated, all grain orientations have the same probability (no texture).

Figure 2 shows an intensity map calculated in the coordinates (2θ; α_i), assuming α_f = 0,5° where 2θ is the in-plane scattering angle. In this map, a part of the Debye ring of Nb110 and Al220 is depicted. The width of the ring in the 2θ direction is inversely proportional to the grain radius R. Along the Debye ring, the intensity modulation follows the dependence of the intensity of the wave-field on α_i; the period of the modulation is inversely proportional to the multi-layer period. The rings Nb110 and Al220 have different structures; these differences are caused by different intensities of the standing wave in Nb and Al layers. Below α_c, the penetration depth of the incoming beam is very small and no diffraction from the grains takes place.

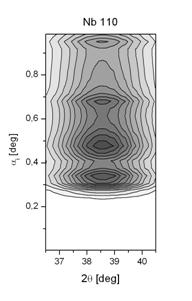
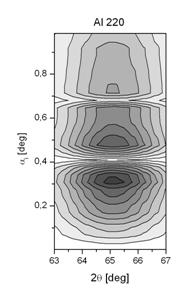
Fig. 2: Calculated intensity for Nb110 and Al220, mean grain size R = 2 nm, α_f = 0,5°.

Figure 3 shows the intensity scans for 2θ = const. calculated for Nb110 and Al220 diffraction and reflection on assuming multi-layer:

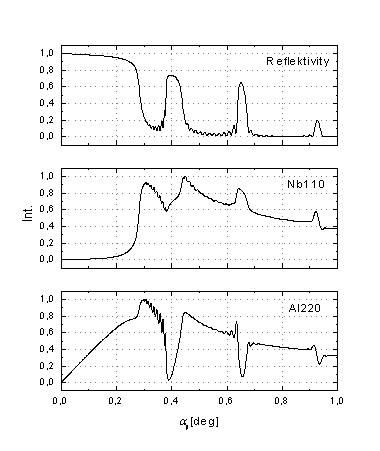
Fig.3: The intensity scans for 2θ = const. for Nb110 and Al220 and reflection on multi-layer, mean grain size R = 2 nm, α_f = 0,5°.

IV. DISCUSSION

Model with flat interfaces (and expectations in paragraph III.) is too simplified to describe real experimental data. The most important point of the further work is description of the scattering process from interfaces roughness. The next problems are the texture, influence of the random size of the grains, etc.

Reference:

[1] S.K. Sinha, E.B. Sirota, S. Garoff, and H.B. Stanley, Phys. Rev. B 38, 2297 (1988).

[2] V. Holý, U. Pietsch, and T. Baumbach, High Resolution X-Ray Scattering from Thin Films and Multilayers, (Springer, Berlin 1999).