Nábojové hustoty a topologická analýza

Miroslav Šlouf, ÚMCH AV ČR, Heyrovského nám. 2, 16206 Praha 6, slouf@imc.cas.cz

Osnova

1. Úvod

2. Nábojové hustoty

2.1. Nábojové hustoty a XRD

2.1.1. Základní teorie

2.1.2. Praktické výpočty

2.2. Nábojové hustoty a QM

2.2.1. Základní teorie

2.2.2. Praktické výpočty

3. Topologická analýza nábojových hustot

3.1. Základní pojmy

3.2. Praktické výpočty v XRD

3.3. Praktické výpočty v QM

4. Závěr

1. Úvod

Rozložení elektronů v krystalu je popsáno funkcí tří proměnných r(x,y,z), která se nazývá elektronová hustota (electron density) nebo nábojová hustota (charge density), přičemž proměnné x, y, z jsou frakční souřadnice. Funkci r(x,y,z) je možno získat z experimentu pomocí rentgenostrukturní analýzy monokrystalů (single-crystal X-ray diffraction; XRD) i z teoretických výpočtů pomocí kvantové mechaniky (quantum mechanics, QM). Elektronová hustota, potažmo funkce r(x,y,z), má určité charakteristické rysy, např. není nikde záporná a nabývá maximálních hodnot v blízkosti atomových jader; studiem těchto a dalších rysů funkce r(x,y,z) se zabývá topologická analýza (topological analysis; TA) nebo podrobněji topologická analýza elektronové (či nábojové) hustoty. TA dokáže pomocí přesně definovaných čísel popsat pojmy jako atomový náboj, iontovost a excentricita vazby, dvojný charakter vazby a podobně.

2. Nábojové hustoty

2.1. Nábojové hustoty a XRD

2.1.1. Základní teorie

V rentgenostrukturní analýze měříme intenzity záření I_hkl difraktovaného na krystalových rovinách (hkl), které jsou úměrné čtvercům absolutních hodnot strukturních faktorů F_hkl:

. (1)

Strukturní faktory jsou obecně komplexní čísla, což můžeme vyjádřit pomocí rovnice:

, (2)

kde j_hkl jsou fáze a |F_hkl| amplitudy strukturních faktorů. Skutečnost, že experiment poskytuje pouze amplitudy |F_hkl|, zatímco k následnému určení krystalové struktury jsou nezbytné hodnoty F_hkl se nazývá fázový problém rentgenostrukturní analýzy, jeho řešení je důkladně popsáno a tento příspěvek se jím nezabývá. Elektronovou hustotu v krystalu r(x,y,z) v místě daném frakčními souřadnicemi (x,y,z) počítáme z hodnot strukturních faktorů:

, (3)

kde sumace probíhá přes všechny indexy h, k, l a V je objem základní buňky. Strukturní faktor z předchozích dvou rovnic udává intenzitu záření rozptýlenou jednou základní buňkou krystalu a získá se jako součet atomových rozptylových faktorů, přičemž je nutno zauvažovat fázové rozdíly a teplotní pohyby atomů:

. (4)

Sčítá se přes všechny atomy j = 1, 2, ...N v buňce. f_j je atomový rozptylový faktor udávající rozptyl záření na j-tém atomu, x_j, y_j a z_j jsou frakční souřadnice atomu a T_j je teplotní faktor popisující vliv teplotního pohybu j-tého atomu. Atomový rozptylový faktor f_j je spojen s elektronovou hustotou r_j na j-tém atomu prostřednictvím Fourierovy transformace:

, (5)

kde S je difrakční vektor udávající směr difraktovaného záření a r je polohový vektor udávající polohu vzhledem k jádru j-tého atomu. Z rovnic (1-5) vyplývá, že nakonec je intenzita difraktovaného záření, měřená při difrakčních experimentech, funkcí elektronových hustot na jednotlivých atomech v krystalu. Různé modely popisované níže se liší právě tím, jakým způsobem definují funkci r_j(r) popisující elektronovou hustotu na atomech:

Vztah pro elektronovou hustotu na atomu	Model	Parametry	Rovnice
rj(r) = ratom(r)	IAM	xj,yj,zj,Tj	(6)
rj(r) = rcore(r) + rval(r,Pv,k)	KR	xj,yj,zj,Tj,Pv,k	(7)
rj(r) = rcore(r) + rval(r,Pv,k) + rdef(r,Plm±,k’)	MR	xj,yj,zj,Tj,Pv,k,Plm±,k’	(8)

Tabulka 1

První model (rovnice 6) se nazývá model nezávislých atomů (Independent Atom Model, IAM) a je základem více než 99% rentgenostrukturních analýz. IAM předpokládá, že atomy v krystalu spolu nijak neinteragují, z čehož plyne, že jsou sféricky symetrické a nenabité. Tato aproximace se může zdát velice hrubá, ale funguje velmi dobře, neboť drtivá většina elektronové hustoty je skutečně sféricky symetrická a soustředěná v bezprostředním okolí jader atomů, jak je podrobněji diskutováno v ref. [1]. Parametry IAM modelu, které se upřesňují metodou nejmenších čtverců (Lest Squares Method, LS) v průběhu řešení struktury, jsou polohy atomů x_j, y_j, z_j a teplotní parametry atomů T_j; soubor poloh atomů a teplotních parametrů je typickým výsledkem IAM (obr. 1).

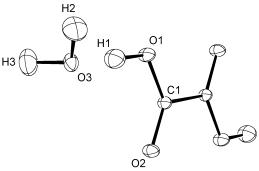
Obrázek 1. Struktura a-dihydrátu kyseliny oxalové [2]. Atomy se nacházejí s 50% uvnitř termálních elipsoidů. Označeny jsou jen atomy ze symetricky nezávislé části, uprostřed C-C vazby je krystalografický střed symetrie.

Druhý model (rovnice 7) je založen na kappa upřesňování (Kappa Refinement, KR, ref. [3]). KR předpokládá, že atomy v krystalu si mohou navzájem vyměňovat elektrony, takže mohou být kladně nebo záporně nabité a mohou též měnit svoji velikost. Atomy nicméně zůstávají sféricky symetrické, jak je patrné z pravé strany rovnice 7, která závisí pouze na vzdálenosti od jádra r, nikoli na vektoru r. V KR se rozdělí atomová el. hustota na elektronovou hustotu příslušející vnitřním a valenčním elektronům (r_core a r_val). Dále se zavedou dva nové parametry: parametr P_v udává skutečný počet valenčních elektronů a parametr k popisuje rozšíření (k < 1) či smrštění (k > 1) valenční slupky vůči izolovanému atomu, pro který platí k = 1. Parametry modelu P_v a k se upřesňují naprosto standardním způsobem pomocí metody LS, společně s polohovými a teplotními parametry atomů. Z parametrů P_v je možno na konci KR vypočíst atomové náboje, které jsou typickým výsledkem této metody.

Třetí model (rovnice 8) je založen na tzv. multipólovém upřesňování (Multipole Refinement, MR, ref. [4]). MR dále rozšiřuje KR tak, že atomy si mohou nejen vyměňovat elektrony a měnit svoji velikost, ale mohou též měnit svůj tvar, tj. mohou jevit odchylky (deformace) od sférické symetrie, které jsou popsány prostřednictvím třetího členu rovnice 8. Parametry P_lm± jsou tzv. multipólové populační parametry, které nabývají hodnot v intervalu <-1;1> a udávají jakým způsobem elektrony porušují sférickou symetrii, parametr k’ souvisí s roztažením či smrštěním deformací a má tedy pro třetí člen rovnice 8 analogický význam jako parametr k pro druhý člen. Všechny parametry modelu (tab. 2) se opět upřesňují metodou LS. Typickým výsledkem MR je v úplný popis elektronové hustoty v krystalu. Narozdíl od IAM a KR popisuje MR i tu část elektronové hustoty, která je v okolí atomů rozmístěna nesféricky, jako např. kovalentní vazby nebo volné elektronové páry (obr. 2). Odtud rovněž plyne, že funkce r(x,y,z) z IAM a KR jsou nekompletní a pro topologickou analýzu je vhodná jedině elektronová hustota z MR.

2.1.2. Praktické výpočty

Výpočty založené na IAM modelu reprezentují naprosto standardní rentgenostrukturní analýzu. K výpočtům je možno použít libovolný relevantní program, např. populární SHELX [5] nebo speciálnější JANA [6]. Funkce r_atom(r) z rovnice 6, popisující elektronovou hustotu na izolovaných atomech jsou známy, jejich Fourierovou transformací dostaneme atomové rozptylové faktory f_j (rovnice 5), které jsou vypočteny a tabelovány v mezinárodních krystalografických tabulkách [7] a příslušné programy [5,6], používají tyto funkce zcela automaticky, aniž by se o to uživatel musel starat.

K výpočtům pomocí modelů KR a MR již potřebujeme speciálnější software, který implementuje rozšíření naznačené v rovnicích 7 a 8. Lze použít původní program MOLLY [3], který je ovšem nepříliš uživatelsky přítulný, novější program XD [8], který je sice uživatelsky přítulnější, ale komerční a konečně program JANA [6], který je volně dostupný a patrně též nejrychlejší a uživatelsky nejpřítulnější. Dále bude popsáno jen MR, a to ze dvou důvodů: za prvé lze KR považovat za zjednodušenou variantu MR a za druhé KR poskytuje atomové náboje, ale ne úplný popis elektronové hustoty v krystalu, který je nutný pro TA.

Při MR upřesňování se postupuje zhruba následujícím způsobem:

(i) Naměříme difrakční data vhodná pro MR, tj. data dostatečně kvalitní (R_obs maximálně kolem 4) vysokoúhlová (do sinq/l ³ 1.0 Å^-1) a nízkoteplotní (nejčastěji se měří při teplotě kolem 100 K).

(ii) Vyřešíme strukturu standardním způsobem pomocí IAM modelu.

(iii) Změníme definice atomových elektronových hustot, tj. změníme fce r_atom (rovnice 6) na funkce r_core a r_val (rovnice 7 a 8).

(iv) Nadefinujeme lokální souřadné systémy (SS) pro jednotlivé atomy. K lokálním SS se vztahuje směr vektoru r z rovnice 8. Je též velmi vhodné nadefinovat lokální symetrii, která významně sníží počet parametrů P_lm±. Například pro uhlíkový atom s hybridizací SP² můžeme nadefinovat lokální trojčetnou osu. Více viz ref. [2].

(v) Upřesníme polohové a teplotní parametry atomů jen s použitím vysokoúhlových dat. Tento krok není nutný, ale je vhodný, protože při vyšších úhlech získáme polohové a teplotní parametry atomů méně ovlivněné vazebnými efekty, což může zlepšit stabilitu metody LS v následujících krocích (podrobněji viz [1,2,9]).

(vi) Zafixujeme polohy a teplotní parametry atomů a metodou LS postupně upřesňujeme další parametry z rovnice 8. Cílem postupného upřesňování je omezit korelace mezi parametry a tak zachovat stabilitu LS. Konečným cílem je upřesnit vše současně. V praxi se osvědčily různé modifikace následujícího postupu: upřesnit jen P_v, k, pak P_v, k, P_lm±, pak jen P_lm±, k’, pak vše současně (někdy s vynecháním parametrů k’). Jsou-li data extrémně kvalitní (což většinou nejsou), lze upřesňovat od začátku vše dohromady.

(vii) Specielní triky, přesahující rámec tohoto pojednání, vyžadují vodíkové atomy, u nichž je hlavní problém nepřítomnost vnitřních (core) elektronů (viz např. [2,3,10]).

(viii) Vykreslíme mapy elektronových hustot, které mohou být buď dynamické (= zahrnující teplotní pohyby atomů) nebo statické (= nezahrnující teplotní pohyby atomů).

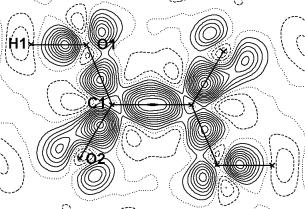
Obrázek 2. Dynamic model deformation electron density map příslušející a-dihydrátu kyseliny oxalové (srovnej s obr. 1). Mapa je diferenční, takže ukazuje rozdíl mezi celkovou elektronovou hustotou a sférickou elektronovou hustotou na atomech. Výsledek rozdílu je nesférická elektronová hustota na atomech, což jsou zde kovalentní vazby mezi atomy a volné elektronové páry na atomech kyslíku O1 a O2. Vrstevnice na mapě jsou po 0.05 eÅ^-3; plné čáry reprezentují kladné, tečkované čáry nulové a přerušované čáry záporné vrstevnice.

2.2. Nábojové hustoty a QM

2.2.1. Základní teorie

Elektronové hustoty v molekulách lze také spočítat pomocí metod kvantové mechaniky. Podle jednoho z postulátů QM je stav systému plně popsán jeho vlnovou funkcí Y. Vlnová funkce stacionárního systému, jako je například molekula v krystalu, může být vypočtena řešením časově nezávislé Schrödingerovy rovnice:

, (9)

která spojuje vlnovou funkci Y s kvantovanou energií systému E prostřednictvím Hamiltonova operátoru . Ačkoli je přesné řešení Schrödingerovy rovnice často obtížné nebo dokonce nemožné, s použitím vhodných aproximací, moderních programů a rychlých počítačů lze vypočítat dosti přesnou vlnovou funkci středně velké molekuly během několika hodin. Jakmile je vypočtena vlnová funkce, lze z ní odvodit další vlastnosti, jako například elektronovou hustotu, která je úměrná čtverci absolutní hodnoty Y v daném místě:

. (10)

2.2.2. Praktické výpočty

QM výpočty jsou dnes, díky neustálému zdokonalování hardwaru i softwaru, přístupné i ne-specialistům v oboru kvantové chemie. Ve skutečnosti jsou běžné QM výpočty z hlediska uživatele jednodušší než odpovídající XRD výpočty. QM výpočty jsou velmi vhodným doplňkem studií nábojových hustot, neboť umožňují ověření výsledků z nezávislého zdroje. Při porovnávání XRD a QM je vhodné si uvědomit důležitou skutečnost: XRD experimenty se týkají molekul v krystalech, zatímco běžné QM výpočty se týkají molekul ve vakuu. U molekulových krystalů, v nichž jsou molekuly vázány jen van der Waalsovými silami, můžeme tento rozdíl zanedbat a používat běžný QM software, jako je GAUSSIAN94 [11], který je v České republice dostupný pro akademické použití zdarma prostřednictvím virtuálního metapočítače [12]. Pro výpočet nábojů a elektronové hustoty v libovoné molekule stačí spustit v programu GAUSSIAN94 následující kód:

#SP

#HF/6-31G**

#P GFInput Iop(6/7=3)

...

Obrázek 3. Výpočet elektronové hustoty v programu GAUSSIAN94.

První řádek (obr. 3) udává typ výpočtu (SP = Single Point = výpočet jen pro jednu geometrii molekuly, žádné optimalizace), druhý řádek udává tzv. level of theory (level of theory je kombinace výpočetní metody (zde HF) a báze atomových orbitalů (zde 6-31G**)), třetí řádek obsahuje klíčová slova modifíkující výstup tak, aby bylo možno zobrazit funkci r(x,y,z) pomocí volně šiřitelného programu MOLDEN [13]. Zbytek souboru (schematicky naznačený třemi tečkami), obsahuje již jen řádek s libovolným titulkem, řádek s nábojem a multiplicitou a řádky s kartézskými souřadnicemi atomů.

3. Topologická analýza nábojových hustot

3.1. Základní pojmy

V kapitole 2 bylo naznačeno, jak získat elektronovou hustotu r(x,y,z), z XRD experimentu (rovnice 1-5, 8) nebo z QM výpočtu (rovnice 9-10). Jedná se o spojitou funkci tří proměnných. Zvolíme-li pro všechny tři proměnné krok 0.1 Å, pak dostaneme pro oxalovou kyselinu (obr. 1) přes 60 tisíc čísel, což je jistě báječné, ale uživatel si spíš klade otázky typu: který ze dvou atomů kyslíku nese větší záporný náboj? Je vazba mezi uhlíkovými atomy dvojná? Odpovědi na tyto otázky poskytuje topologická analýza [14].

Máme-li funkci r(x,y,z) = r(x₁,x₂,x₃) = r(r), můžeme z ní vypočítat řadu dalších věcí: první derivace (dr(r)/dx_i), druhé derivace (d²r(r)/dx_idx_j), gradient (Ñr(r)), laplacián (Ѳr(r)), matici H(r) (matice 3x3, jejíž prvky jsou druhé derivace d²r(r)/dx_idx_j tzv. Hessian matrix), vlastní hodnoty H(r) (l₁, l₂, l₃: tzv. křivosti (curvatures)). Zatím jsme jen zkomplikovali situaci dalšími horami čísel, ale v následujících krocích vše využijeme ke zjednodušení.

Gradient Ñr(r) je vektor, který ukazuje ve směru největšího nárůstu funkce r(r). Nyní začněme v libovolném místě r poblíž molekuly, vypočtěme gradient, posuňme se ve směru gradientu o element délky, vypočtěme další gradient, posuňme se atd. Takto nakonec dostaneme křivku, která dříve nebo později skončí na nějakém atomovém jádře, kde je lokální maximum funkce r(r) a odkud už není kam jít. Všechny body r z okolí molekuly, ze kterých se tímto způsobem dostaneme k danému jádru, jednoznačně vymezují jakousi oblast (basin) příslušející danému atomu. V této oblasti provedeme integraci elektronové hustoty a dostaneme atomový náboj.

Ukazuje se, že nejdůležitějšími prvky funkce r(r) jsou takzvané kritické body (Critical Points; CP), kterých je v každé molekule či elementární buňce jen několik a nacházejí se v místech, kde jsou všechny první derivace nulové (dr(r)/dx_i = 0). CP se dále charakterizují pomocí pomocí křivostí l₁, l₂, l₃: každý CP je označen dvěma čísly, z nichž první udává počet nenulových křivostí (v případě stabilní molekuly vždy 3) a druhé udává součet znamének křivostí (zde jsou čtyři možnosti, viz např. [14,15]). Každé mapě elektronové hustoty dominují maxima na atomových jádrech, což jsou podle TA kritické body (3,-3). Z chemického hlediska jsou nejzajímavější sedlové body vazeb, z hlediska TA jde o CP (3,-1), tzv. kritické body vazby (Bond Critical Points; BCP). Pomocí hodnot výše definovaných funkcí v místě BCP lze každou vazbu kvantitativně popsat. Např. dvojný charakter vazby lze získat pomocí hodnoty veličiny zvané elipticita (elipticity: e = l₁/l₂ - 1) v BCP, která se liší od nuly tím víc, čím víc se vazba blíží dvojné.

3.2. Praktické výpočty v XRD

Máme-li vypěstován nadprůměrně kvalitní krystal (což je patrně nejobtížnější), změřena vysoce kvalitní difrakční data (rovněž netriviální úkol) a provedené multipólové upřesnění (relativně snadné, viz kapitola 2.1.2) jsou výpočty týkající se topologické analýzy v programu JANA z uživatelského hlediska velmi jednoduché. Pro výpočet atomových nábojů stačí zadat z grafického menu: Tools ® Topological analysis ® Basin integration a projít několika intuitivními dialogovými okny. Analogicky pro vyhledání CP a výpočet všech příslušných hodnot stačí v JANĚ zadat: Tools ® Topological analysis ® Find critical points.

3.3. Praktické výpočty v QM

Výpočet atomových nábojů přímou integrací funkce r(x,y,z) a všech patřičných veličin ve všech CP libovolné molekuly zajistí v programu GAUSSIAN94 následující kód:

#SP

#HF/6-31G**

#AIM=(Charges,CP)

...

Obrázek 4. Výpočet atomových nábojů a CP v programu GAUSSIAN94.

První dva příkazy na obr. 4 jsou identické s obr. 3 (kapitola 2.2.2), příkaz na třetím řádku říká programu, že má provést topologickou analýzu s výpočtem nábojů a určením kritických bodů, zbytek souboru na obr. 4 je opět totožný s obr. 3.

4. Závěr

Tento příspěvek, vzhledem ke své omezené délce, nemůže pokrýt celou problematiku spojenou s nábojovými hustotami a topologickou analýzou a suplovat tak objemné učebnice [15, 16] či obsáhlé souhrné články [17, 18]. Jedná se o velmi stručný úvod do problematiky, která může být zajímavá esteticky (viz obr. 2), teoreticky (přímé srovnání QM a XRD) i prakticky (využití informací o atomových nábojích při syntézách). Vše bylo velmi zjednodušeno, úplně vynechána byla mj. pasáž týkající se X-X a X-N upřesňování [9] a klíčová pasáž zabývající se měřením XRD dat vhodných pro studium nábojových hustot (viz minulé kolokvium, ref. [19]). Topologická analýza [14] byla jen naznačena. Pro podrobnější informace je třeba odkázat na výše zmíněné učebnice a články [15-18], popřípadě i na autorovu disertační práci [2] a souhrnné články v češtině [19, 20].

Literatura

[1] V. Valvoda: Experimentální metody studia pevných látek. Rentgenová difrakce: struktury, nábojové hustoty, vazby. (Lukáč P., ed.), sv. 3, Matematicko-fyzikální fakulta UK, Praha 1981.

[2] M. Šlouf: Disertační práce & odkazy v ní uvedené. Karlova univerzita, Praha 2001.

[3] P. Coppens, T.N. Guru Row, P. Leung, E.D. Stevens, P.J. Becker & Y.W. Yang, Acta Cryst. A35,(1979) 63.

[4] N.K. Hansen & P. Coppens, Acta Cryst. A34 (1978) 909.

[5] G.M. Sheldrick (1997). SHELX-97. Programs for X-ray structure determination and refinement. University of Gottingen, Germany.

[6] V. Petříček & M. Dušek (2000). JANA2000. Crystallographic Computing System. Institute of Physics, Praha, Czech Republic.

[7] International Tables for Crystallography (1995). Vol. C, edited by A.J.C. Wilson. Dodrecht: Kluwer.

[8] T. Koritsanszky, S. Howard, Z. Su, P.R. Mallinson, T. Richter, & N.K. Hansen (1997). XD. Computer Program Package for Multipole Refinement and Analysis of Electron Densities from Diffraction Data. Free University of Berlin, Germany.

[9] J. Loub, Chem. Listy 78 (1984) 720.

[10] M. Šlouf, A. Holý, V. Petříček, & I. Císařová, Acta Cryst. B58 (2002) 519.

[11] M.J. Frisch, G.W. Trucks, H.B. Schlegel, P.M.W. Gill, B.G. Johnson, M.A. Robb, J.R. Cheeseman, T. Keith, G.A. Petersson, J.A. Montgomery, K. Raghavachari, M.A. Al-Laham, V.G. Zakrzewski, J.V. Ortiz, J.B. Foresman, J. Cioslowski, B.B. Stefanov, A. Nanayakkara, M. Challacombe, C.Y. Peng, P.Y. Ayala, W. Chen, M.W. Wong, J.L. Andres, E.S. Replogle, R. Gomperts, R.L. Martin, D.J. Fox, J.S. Binkley, D.J. Defrees, J. Baker, J.P. Stewart, M. Head-Gordon, C. Gonzalez, and J.A. Pople, Gaussian 94, Revision D.4, Gaussian, Inc., Pittsburgh PA, 1995.

[12] http://meta.cuni.cz/

[13] G. Schaftenaar & J.H. Noordik, J. Comput.-Aided Mol. Design, 14 (2000) 123.

[14] R.F.W. Bader: Atoms in Molecules: a Quantum Theory. Oxford 1990. Clarendon Press, Oxford Science Publications.

[15] P. Coppens: X-ray Charge Densities and Chemical Bonding. New York 1997. Oxford University Press.

[16] V.G. Tsirelson & R.P. Ozerov: Electron Density and Bonding in Crystals. Bristol, England / Philadelphia, PA 1996. Institute of Physics Publishing.

[17] P. Coppens, Acta Cryst. A54 (1998) 779.

[18] G.U. Kulkarni, R.S. Gopalan & C.N.R. Rao, J. Mol. Struct. (Theochem) 500 (2000) 339.

[19] M. Šlouf, Materials Structure, 9(1) (2002) 26.

[20] M. Šlouf, Chem. Listy 96 (2002) 3.