ANALÝZA PROFILŮ RTG DIFRAKČNÍCH LINIÍ

Zdeněk Matěj

Univerzita Karlova, Matematicko-fyzikální fakulta, 121 16 Praha 2, Ke Karlovu 5

Jemnozrnné materiály s nano- a submikro-krystalickou strukturou vykazují řadu zajímavých vlastností. Jednou z experimentálních metod jejich studia je i rentgenová difrakce, především studium tvaru (rozšíření) difrakčních profilů. Rentgenová difrakce může poskytnou cenné informace především o tzv. reálné struktuře takových materiálů. Existuje řada metod analýzy difrakčních profilů. V posledních letech se objevilo i několik metod novějších a několik programů určených k analýze difrakčních profilů takových materiálů. Tyto programy byly použity k analýze mikrostruktury vzorků submikro-krystalické mědi získaných silnou plastickou torzní deformací za vysokého tlaku. Bylo nutné řešit i problém dekonvoluce difrakčních dat.

Tradiční metodou analýzy difrakčních profilů je metoda Williamsonova-Hallova grafu a analýza Fourierových koeficientů Warrenovou-Averbachovou metodou. Obě metody lze modifikovat tak, že více souvisí přímo s mikrostrukturou zkoumaného vzorku. Kromě rozšíření profilů vlivem malé velikosti krystalitů a přítomnosti mřížových deformací způsobených přítomností dislokací v materiálu lze zahrnout i vliv vrstevných poruch. Vysvětlit je možno anizotropii rozšíření difrakčních linií a asymetrii profilů. Při analýze rozšíření difrakčních profilů je potřeba mít model mikrostruktury materiálu. Parametry modelu je potom možné z naměřených dat určit a zpřesnit. K popisu velikostního efektu rozšíření difrakčních profilů se nejčastěji používá model kulových krystalitů o průměru D. Rozdělení velikosti krystalitů lze většinou dobře popsat pomocí Log-normálního rozdělení jejich průměru D (obr. 1).

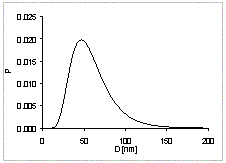
Obr. 1 : Log-normální rozdělení velikosti krystalitů.

Deformační rozšíření profilů je možné popsat pomocí modelu „omezeně náhodně rozdělených dislokací”, který vypracoval Wilkens. Na základě takového modelu mikrostruktury je možné vypočítat Fourierovy koeficienty všech difrakčních linií, jejich profily a nakonec i celý difrakční záznam. Připodobňováním vypočtených hodnot a naměřených dat lze určovat a zpřesňovat parametry modelu podobně jako při kvantitativní fázové analýze Rietveldovou metodou. Toho využívají nejnovější metody a programy. Jeden z nich - program MWP-fit (viz. [1], [2]) - je založen na fitování fyzikálních profilů (očištěných od vlivů měřících přístrojů) na základě mikrostrukturního modelu. V jiném programu – PM2000 (viz [3], [4], [5]) se fituje celý naměřený záznam, podobně jako např. ve FullProfu, a zpřesňují se přímo parametry mikrostrukturního modelu. Aby bylo možno provádět Warrenovu-Averbachovu analýzu, nebo použít program MWP-fit, je nezbytné odstranit vliv instrumentálního rozšíření difrakčních profilů, provést dekonvoluci. Program PM2000 počítá konvoluci vypočtených fyzikálních profilů a zadané instrumentální funkce a výsledek porovnává přímo s naměřenými daty. Problém dekonvoluce tak obchází konvolucí.

Všechny uvedené metody byly použity ke sledování změn mikrostruktury vzorků submikro-krystalické mědi v procesu isochronního žíhání. Parametry mikrostrukturního modelu získané metodou modifikované Warrenovy-Averbachovy analýzy (obr. 2) byly zpřesněny v programech MWP-fit a PM2000. Byly porovnány získané výsledky (obr. 3) a zvážena jejich věrohodnost. Tyto nové, důmyslnější metody analýzy difrakčních profilů jsou vcelku spolehlivé při oddělování velikostního a deformačního rozšíření. Problémy jsou s korelací hustoty dislokací a parametru, jenž popisuje jejich uspořádání. Vypočtené profily nepopisují zcela dobře naměřená data. Bylo by proto vhodné mikrostrukturní model pro zkoumané vzorky upravit.

Vedle vlastních metod profilové analýzy byla vyzkoušena a porovnána řada metod určených k dekonvoluci difrakčních dat (kapitola M. Čerňanského v [6]). Byly vyzkoušena jednoduchá dekonvoluce pomocí Fourierovy transformace, dekonvoluce založená na použití inverzních, optimálních (Wienerových) filtrů (viz. [6], [7]), metody, které počítají naměřený profil jako lineární kombinaci instrumentálního profilu (viz. [8]), metody regularizace a Kojdeckého algoritmus (viz. [9]).

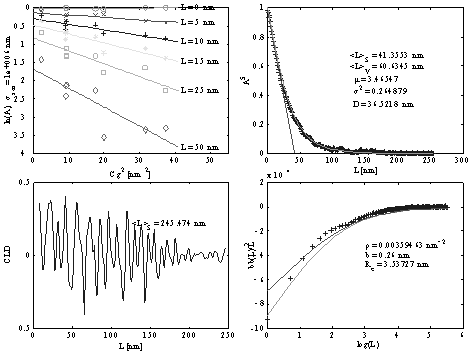
Obr. 2 : Modifikovaný Warrenův-Averbachův graf (vlevo nahoře), analýza velikostních Fourierových koeficientů (vpravo nahoře), analýza deformačních Fourierových koeficientů (vpravo dole).

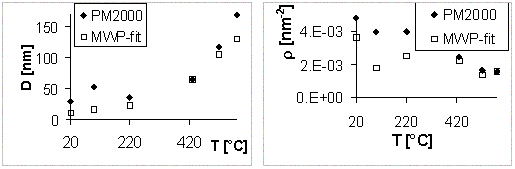
Obr. 3 : Výsledky zpřesňování velikosti krystalitů D a hustoty dislokací r vzorků mědi žíhaných při různých teplotách.

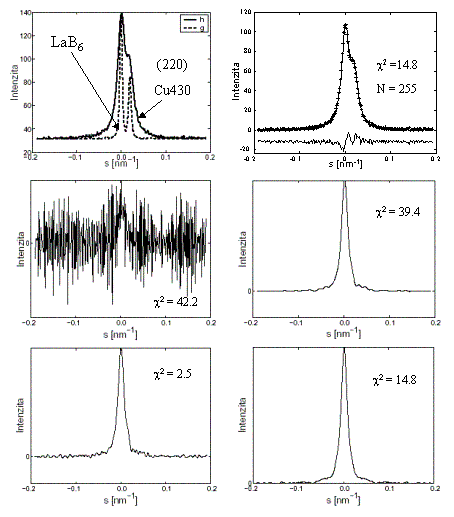
Obr. 4 : Ukázka výsledku získaných několika metodami dekonvoluce. Nahoře je naměřený a instrumentální profil a ukázka shody měřeného profilu a konvoluce instrumentální funkce s fyzikálním profilem získaným dekonvolucí.

[1] T. Ungár, J. Gubicza, G. Ribárik, A. Borbély, J. Appl. Cryst. 34 (2001) 298-310.

[2] G. Ribárik, T. Ungár, J. Gubicza , J. Appl. Cryst. 34 (2001) 669-676.

[3] P. Scardi, M. Leoni, Acta Crystallographica A57 (2001) 604-613.

[4] P. Scardi, M. Leoni, Y.H. Dong, Eur. Phys. J. B 18 (2000) 23-30.

[5] P. Scardi, M. Leoni, Acta Crystallographica A58 (2002) 190-200.

[6] M. Čerňanský : Restoration and preprocessing of physical profiles from measured data.

v R.L. Snyder, J. Fiala & H.J. Bunge (eds.) Defect and Microstructure Analysis by Diffraction. Oxford 1999. IUCr/Oxford University Press.

[7] W. H. Press, S. A.Teukolsky, W. T. Vetterling , B. P. Flannery : Numerical Recipes in C. 2nd ed. Cambridge 1992. Cambridge University Press.

[8] D. Rafaja, Materials Structure 7(2) (2000) 43-50.

[9] M. A Kojdecki, Materials Science Forum Vols. 378-381 (2001) 12-17.