ŘEŠENÍ KRYSTALOVÝCH STRUKTUR Z PRÁŠKOVÉ DIFRAKCE

Radovan Černý

Laboratoire de Cristallographie, Université de Genève, 24 quai Ernest-Ansermet, CH-1211 Genève 4, Suisse

Úvod

Ne vždy máme pro určení neznámé krystalové struktury k dispozici kvalitní monokrystal. Typickým případem jsou kovové slitiny a jejich intermetalické fáze, hydridy techto fází, některé molekulární krystaly a řada dalších. Byly to molekulární materiály, zvláště farmaceutické látky, které motivovaly v posledních 20 letech intenzivní vývoj v teorii i experimentu difrakčních metod používajících polykrystalický vzorek. Celkový počet krystalových struktur určených těmito metodami se pohybuje někde okolo 600 s roční produkcí vyšší než 50 (http://www.cristal.org/iniref.html). A přiznejme si, že vzrůstající síla těchto metod někdy vede k poklesu intensity práce v přípravě materiálu, neboť je rychlejší připravit polykrystalický vzorek než strávit řadu týdnů na přípravě dostatečně velkého monokrystalu (i když monokrystalové difraktometry při zdrojích synchrotronového záření posouvají potřebnou velikost monokrystalu stále dolů). Prášková difrakce nemůže nikdy dosáhnout prostorového rozlišení a strukturní přesnosti difrakce monokrystalové. Pracuje totiž s 1-rozměrnou projekcí původně 3-rozměrného difrakčního obrazu v reciprokém prostoru, která nutně vede k překryvu nezávislých informací i v ideálním případě difraktometru s nekonečně velkým úhlovým rozlišením. Prášková difrakce se může ve výkonosti pouze približovat difrakci monokrystalové a může těžit ze širokého arzenálu metod zde již existujících. Nižší rozlišení měřených dat práškové difrakce však vedlo k vývoji netradičních metod řešení struktur (globální optimalizace), které našly svou inspiraci v jiných oblastech výzkumu setkávajících se s podobným problémem: Obtížností přímé cesty od dat, která je možno měřit, k hodnotám hledaných parametrů.

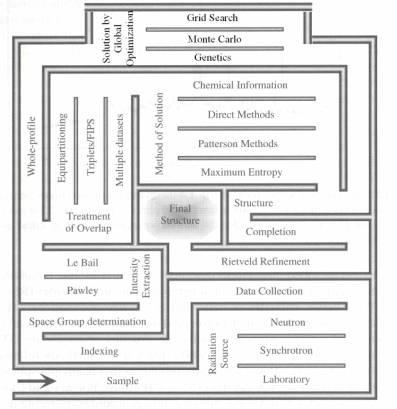
Obr. 1: Bludiště řešení krystalové struktury; modifikováno z [1].

Současný limit práškové difrakce je asi 30 atomů v asymetrické buňce pro rutinní práci, struktury se 60 atomy už byly vyřešeny. Optimisté odhadují, že brzy můžeme dosáhnout limitu 100 atomů (http://www.sacrs.org.za/ecm21/plenary.html). Řešení krystalové struktury může být přirovnáno k bludišti (obr. 1): I když k cíli (struktuře) vede více cest, ne všechny jsou vhodné či dokonce možné pro daný problém. Základními etapami, komorami v bludišti, však musí projít každý, má však možnost volby mezi různými cestičkami. O některých z nich pojednává tento příspěvek. Nebudeme se zabývat přípravou vzorku a optimalizaci difrakčního experimentu ani poslední etapou – vypřesnění struktury pomocí Rietveldovy metody.

Indexace práškového difrakčního záznamu

První, a ne vždy lehký krok, je určení elementární buňky našeho neznámého krystalu – indexace difrakčního záznamu. Ve srovnání se monokrystalovými daty je to úloha o to těžší, že nemáme k dizpozici informaci o orientaci reciprokých vektorů r^*_hkl, ale jenom o jejich délce 1/d_hkl. Základní soustavou rovnic, se kterou pracují všechny indexační algoritmy práškových dat je

Q_hkl = 1/d²_hkl = h²a^*2 + k²b^*2 + l²c^*2 + 2hka^*b^*cosg^* + 2klb^*c^*cosa^* + 2hla^*c^*cosb^* (1)

čili pro každou pozorovanou hodnotu Q_hkl (danou polohou jedné reflexe hkl v práškovém difrakčním záznamu) máme najít tři celá čísla (Millerovy indexy hkl) a šest mřížových parametrů stejných pro celou soustavu rovnic. Rovnice (1) nabývá jednodušších forem pro vyšší symetrie krystalové mříže. Hodnoty Q_hkl jsou měřeny s určitou přesností, tudíž teoreticky by bylo možné oindexovat každý difrakční záznam pomocí kubické elementární buňky s mřížovým parametrem ~ 10⁵ Å, což samozřejmě není správné řešení. Čili bez ohledu na to jak indexujeme difrakční záznam, potřebujeme jednoduché kriterium pro fyzikální správnost řešení. Takový parametrem je de Wolffovo kriterium (Figure-of-Merit)

M₂₀ = Q₂₀ / (2 <Q> N₂₀) (2)

kde pracujeme s prvními 20 pozorovanými a oindexovanými reflexemi, Q₂₀ je Q hodnota pro 20-tou reflexi, <Q> je průměrný rozdíl mezi pozorovanými a spočtenými Q hodnotami a N₂₀ je počet spočtených reflexí až do pozorované 20-té reflexe. Hodnota M₂₀ > 10 značí s velkou pravděpodobností fyzikálně správné řešení. Jiným kriteriem je Smithův a Snyderův F-index

F_N = 1 / <D2q> × N / N(q_g) (3)

kde pracujeme s pozorovanými reflexemi až do úhlu q_g, N je počet pozorovaných a N(q_g) počet spočtených reflexí až do tohoto limitu a <D2q> je průměrný rozdíl mezi pozorovanými a spočtenými hodnotami 2q. Na rozdíl od M₂₀ nezávisí F_N na symetrii krystalové mříže, což však není vždy výhoda neboť kubické řešení je pravděpodobnější než triklinické pro stejný počet oindexovaných reflexí a stejnou přesnost poloh reflexí. Pro spravný výpočet M₂₀ a F_N by měly být vzaty v úvahu systematické absence, což je možné až po určení prostorové grupy. Úspěšnost indexace, tak jako celého procese určení struktury, závisí silně na kvalitě měřených dat včetně včasné identifikace reflexí příměsových fází. Obtížný je případ indexace krystalové mříže s dominantní zonou – jedna krystalová osa podstaně kratší než ostatní dvě.

Vlastní indexační proces používá různé algoritmy jak vyřešit soustavu, typicky 20-ti, rovnic (1) a provádí inteligentní nebo vyčerpávající hledání v přímém (mřížové parametry) nebo reciprokém (Millerovy indexy) prostoru. Program ITO [2] využívá toho, že reflexe náležijící stejné centrální zoně (rovina v reciprokém prostoru procházející počátkem) lze oindexovat pomocí pouze dvou indexů a hledá takové zony v pozorovaných datech. Program DICVOL91 [3] provádí vyčerpávající hledání v přímém prosotoru a využívá přitom principu dichotomie: systematicky hledá oblasti hodnot mřížových parametrů, které mohou obsahovat řešení a vylučuje ostatní oblasti. Program TREOR90 [4] provádí vyčerpávající hledání v reciprokém prostoru a využívá přitom určitého stupně inteligence plynoucího z předchozích zkušeností. CRYSFIRE (http://www.ccp14.ac.uk/tutorial/crys/index.html ) je rozhraní k více indexačním programům s analyzou výsledků. Jelikož řešení mnohaparametrové soustavy rovnic (1) je typický problém globální optimalizace, není překvapující, že se objevila řada indexačních programů uživajících algoritmy globální optimalizace jako metody Monte Carlo, genetický algoritmus a jiné. Přehled všech metod a odkazy na jednotlivé programy lze najít v (http://www.ccp14.ac.uk/solution/indexing/index.html).

Vlastní proces úspěšné indexace musí být zakončen prověřením správnosti nalezené elementární buňky pomocí Whole-Pattern-Profile-Fitting, tak jak je popsán v následující kapitole, a rovněž i redukcí buňky a nalezením buňky Bravaisovy, která vykazuje přijatelné systematické absence.

Určení prostorové grupy a integrovaných intenzit jednotlivých reflexí

Základní problem práškové difrakce, 1-rozměrná projekce původně 3-rozměrného difrakčního obrazu, vede k částečnému či úplnému překryvu reflexí v difrakčním záznamu. Obtížnost pracovat s integralními intenzitami jako s nezávislými pozorováními vedla H. Rietvelda [5] ke slavné metodě nesoucí dnes jeho jméno, modelování celého digitálního práškového difrakčního záznamu, a užití každého bodu jako nezávislého pozorování. Tento přístup lze také nazvat Whole-Pattern-Profile-Fitting (WPPF) a má dvě varianty: (a) užívající strukturní model – vlastní Rietveldova metoda, (b) bez strukturního modelu – metoda Le Bailova [6] nebo Pawleyho [7]. Je dobré si uvědomit, že (a) je ve své podstatě vypřesňovnání strukturních parametrů z dat práškové difrakce, zatímco (b) slouží hlavně k dekompozici práškového difrakčního záznamu na jednotlivé integrální intenzity. Obě metody, (a) i (b), však mají mnoho společného, takže je vždy najdeme jako součast jednoho výpočetního programu. Nebudeme zde podávat matematický základ Rietveldovy metody, to lze najít v příslušné kapitole tohoto přehledu, budeme se zde zabývat pouze metodou (b) neboť lze pomocí ní ověřit správnost indexace, získat informace o systematických absencích – prostorové grupě krystalu a získat jednotlivé integrální intenzity.

Metoda Le Bailova je WPPF bez strukturního modelu, avšak s mřížovými parametry a prostorovou grupou (pro začátek to může být grupa holoedrie). Mřížové parametry, profilové parametry (šířky a tvar reflexí) a instrumentální parametry (kalibrace 2q, pozadí) jsou upřesňovány (např. metodou nejmenších čtverců) a hodnoty integrálních intenzit jsou upřesňovány pomocí iterativní metody založené na původním Rietveldově vztahu pro výpočet pozorovaných integrálních intenzit. Při iterování se pozorované intenzity z n-té iterace stávají vypočtenými intenzitami pro (n+1)-tou iteraci, přičemž počáteční hodnoty vypočtených intenzit v 0-té iteraci odpovídají např. rovnoměrnému rozdělení celkové intenzity mezi překrývající se reflexe. Metoda Pawleyho se liší tím, že integrální intenzity jsou považovány za volné parametry a jsou upřesňovány současně se všemi ostatními volnými parametry.

Úspěšně provedené La Bailovo nebo Pawleyho vypřesnění slouží v prvé řadě pro prověření správnosti elementární buňky, dále pro získání informací o systematických absencích a nakonec i pro získání hodnot pozorovaných integrálních intenzit I_hkl(obs) jednotlivých reflexí pro jejich další použití při určení krystalové struktury pomocí metod monokrystalových. Určení prostorové grupy z práškových dat se ve své podstatě řídí stejnými pravidly jako pro data monokrystalová. Překryv jednotlivých reflexí v práškovém difrakčním záznamu však způsobí omezení pouze na nízkoúhlové reflexe a prakticky znemožní určení ze statistiky intenzit zda prostorová grupa obsahuje střed symetrie. Užití celého difrakčního záznamu a zkoumání systematických absencí pomocí Bayesovy teorie pravděpodobnosti [8] znamená mnohem kompletnější analyzu. Pro určení integrálních intenzit I_hkl(obs) pomocí WPPF musíme rozhodnout jak budeme zacházet s částečně a úplně se překrývajícími reflexemi. O nových metodách založených na užití dodatečné krystalografické informaci anebo na dodatečném experimentu pojednává následující kapitola.

Metody určení integrovaných intenzit překrývajících se reflexí

Užití dodatečné krystalografické informace (atomicita a pozitivnost)

Během procesu určovaní fází reflexí jejichž integrální intenzity již byly spolehlivě určeny (nepřekrývající se reflexe) získáme řadu dodatečných informací, které můžeme použít pro separaci překrývajících se reflexí. Informace o pseudo-translační symetrii byla použita v programu EXPO [9]: Překrývají-li se reflexe super-struktury s reflexí sub-struktury, je pravděpodobnější, že druhá bude mít větší intenzitu. Užití fázové informace již lokalizované částečné struktury (molekulární fragment) se provádí ve stejném programu. Uzití informace o strukturních invariantech se užívá v programu DOREES-POWSIM [10]: Známe-li již moduly dvou reflexí v silném tripletu çE_kça çE_h+kçmůžeme s velkou pravděpodobností tvrdit, že modul třetí reflexe v tripletu, çE_hç, bude rovněž velký.

Očekávaná pozitivnost Pattersonovy funkce v přímém prostoru: Pattersonova funkce spočtena z dat, která jsou k dispozici (nepřekrývající se reflexe), je ne-lineárním způsobem modifikována, přičemž je Pattersonově funkci vnucena pozitivnost. Z této modifikované Pattersonovy funkce pak můžeme zpětnou transformací obdržet druhé mocniny modulů všech reflexí, tedy i překrývajících se. Tyto nové odhady pak mohou sloužit jako nové počáteční hodnoty pro Le Bailovu metodu anebo celý proces může být iterativně opakován. Pattersonova mapa může být modifikována na základě principu maximální entropie [11] anebo na základě Sayerova argumentu „Druhá mocnina Fourierovy mapy je podobná Fourierově mapě samotné“ aplikovaného v iterativní podobě jako Fast-Iterative-Patterson-Squaring v [12].

Užití dodatečného experimentu – více difrakčních záznamů

Měřením více difrakčních záznamů na jednom vzorku při různých, ale kontrolovaných, vnějších podmínkách můžeme získat více informace o intenzitách překrývajících se reflexí. Vztah mezi difrakčními záznamy musí být znám anebo měřitelný. Dva případy měněných vnějších podmínek byly úspěšně aplikovány: teplota a textura.

Máme-li materiál s anisotropní teplotní roztažností potom relativní intenzity reflexí se téměř s teplotou nemění, avšak jejich relativní polohy ano. Tím se mění i obraz překryvu reflexí a měřením difrakčních záznamů při různých teplotách obdržíme dodatečnou informaci, která může pomoci separaci reflexí. Tato myšlenka byla poprve použita již v [13] a v moderní podobě v [14].

Tak jako anisotropní teplotní roztažnost mění anisotropně polohy reflexí s teplotou, tak textura (přednostní orientace krystalitů) mění anisotropně intenzity reflexí se změnou orientace difrakčního vektoru. Podmínkou využití textury k separaci překrývajících se reflexí je texturovaný vzorek a znalost textury (např. jejím změřením na nepřekrývajících se reflexích). Máme-li potom n překrývajících se reflexí tak, že můžeme pouze určit jejich souhrnou intenzitu I_tot, můžeme získat jejich integrální intenzity I_i (i = 1 ... n) řešením soustavy rovnic (4) můžeme-li určit texturní korekci T_i(a_j). Parametr a_j označuje m měření difrakčního záznamu při m různých orientacích difrakčního vektoru vůči vzorku, např. náklon vzorku o úhel a_j na texturním goniometru.

I_tot (a₁) = I₁ T₁(a₁) + I₂ T₂(a₁) + ... + I_n T_n(a₁)

I_tot (a₂) = I₁ T₁(a₂) + I₂ T₂(a₂) + ... + I_n T_n(a₂)

.............................................................................................. m ≥ n (4)

I_tot (a_m) = I₁ T₁(a_m) + I₂ T₂(a_m) +... + I_n T_n(a_m)

Textura jako nástroj pro zisk maximální informace z práškové difrakce byla navržena a poprvé využita v [15] a úspěšně použita v [16, 17].

Metody řešení krystalové struktury vyžadující integrované intenzity – metody reciprokého prostoru

Přímé metody

Přímé metody založené na teorii pravděpodobnosti fází pozorovaných strukturních faktorů známe-li jejich moduly, se vyvinuly v mocný nástroj určování krystalových struktur z monokrystalových dat. Nic nám nebrání, pokud se nám podaří získat integrální intenzity jednotlivých reflexí, aplikovat stejné metody na prášková data. Přímé metody vyžadují pro svou úspěšnou funkci kvalitní data s rozlišením odpovídajícím typické meziatomové vzdálenosti v krystalu (~1 Å pro organické látky, nižší rozlišení pro latky s těžkým atomem), což může být problém pro prášková data díky vzrůstajícímu překryvu reflexí se vrůstajícím difrakčním úhlem. Díky menší přesnosti modulů strukturních faktorů získaných z práškových dat a jejich možnému systematickému ovlivnění metodou separace překrývajích se reflexí, standardní statistické testy přímých metod (Wilsonův test, rozdělení normalizovaných modulů, Figures-of-Merit) nemusí vždy spolehlivě fungovat. Dva výpočetní programy přímých metod byly optimalizovány pro užití práškových dat, POWSIM [10] a EXPO [9]. Dekompozice práškového záznamu je jejich integrální součástí, tak jak je diskutováno v předchozí kapitole. Jiný způsob využití teorie, která je základem přímých metod, je maximalizace Sayreovy rovnice vzhledem k fázím, kde je v součtové funkci modulů Pattersonova typu odstraněno maximum v počátku [18].

Pattersonova funkce

Pattersonova funkce byla s úspěchem použita již v raném období práškové difrakce, protože zvláště při aplikaci na struktury obsahující těžký atom je tato metoda robustní a funguje i s daty s nízkým rozlišením. Čitelnost Pattersonových map je však omezena jejich “rozmazáním“ díky problemům uvedeným v předchozím odstavci. Čitelnější mapy lze obdržet z neutronové difrakce zvláště v případě přítomnosti atomu s negativním rozptylovým faktorem. Elegantní způsob “zaostření“ Pattersonových map z práškové difrakce je uveden v [11]. Celková intenzita skupiny překrývajících se reflexí je považována za jeden údaj a digitalizována Pattersonova mapa je rekonstruována na principu maximální entropie tak jak je známo v metodách rekonstrukce obrazu. Stejná procedura může rovněž sloužit ke zlepšení rozdělení celkové intenzity skupiny mezi jednotlivé reflexe, tak jak je uvedeno v předchozí kapitole.

Maximalizování entropie

Princip maximalizování entropie může být uplatněn přímo v procesu konstrukce map elektronových hustot. Ukázalo se [19], že tento přístup je obzvláště užitečný pro data z nižším rozlišením - data z práškové difrakce. Fázování všech strukturních faktorů ze základního souboru se provádí na základě maximalizování vhodné pravděpodobnostní (likelihood) funkce a stejný princip lze použít i pro separaci překrávajících se reflexí. Celý proces lze najít ve výpočetním programu MICE [20].

Metody řešení krystalové struktury globální optimalizací strukturního modelu a kompletního difrakčního obrazu – metody přímého prostoru

Základní problém práškové difrakce, obtížnost získání kvalitních odhadů intenzit jednotlivých reflexí, lze obejít tím, že se o žádné odhady nebudeme pokoušet. Místo analýzy (rozkladu) difrakčního obrazu přejdeme k jeho syntéze (simulaci) s “náhodným“ (zde můžeme vložit do procesu dodatečnou chemickou či jinou informaci a zvýšit tak jinak značně deficitní informační obsah dat) strukturním modelem, který dále optimalizujeme vhodným algoritmem globální optimalizace. Můžeme na základě Rietveldova principu porovnávat celý difrakční profil, anebo počítat jenom integrované intenzity a porovnávat je s korelovanámi integrálními intenzitami získanými z WPPF. Pro rozhodování o vhodnosti (fitness) aktuálního strukturního modelu musíme zavést funkci, která bude vhodnost charakterizovat - cost function (CF). Může to být např. parametr R_wp známý z Rietveldovy metody nebo lépe parametr c²

c² = D/(M - N) D = å_i=1…M wⁱ [y_obsⁱ - y_calⁱ]² (5)

kde y_obs a y_cal jsou pozorované, s vahou w, a spočtené intenzity v bodě i digitálního difrakčního záznamu a D je kvadratická forma minimalizovaná v Rietveldově metodě pomocí metody nejmenších čtverců pro M pozorování a N volných parametrů. Parametr c² je vhodnější z důvodu správnější vážené kombinace CF založené na difrakčních datech s CF založené na dodatečných informacích. Při práci s korelovanými integrálnímí intenzitami je takovou CF např. [21]

c² = å_h å_k [(I_obs^h - I_cal^h) (V^hk)^-1 (I_obs^k - I_cal^k)] (6)

kde I_obs^h a I_cal^h jsou pozorované a spočtené integrální intenzity reflexe h a V^hk je matice kovariancí integrálních intenzit reflexí h a k z WPPF (Pawleyho metoda).

CF založené na difrakčních datech mohou být kombinovány s CF založenými na dodatečných pozorováních či chemických informacích. Kombinování (např. součet CF) musí být váženo, správná kvantifikace váh je stále objektem diskuse v literatuře. Nejčastěji používanou ne-difrakční CF je energie krystalové mříže, nejčastěji pro tyto účely popisovaná potenciální energií aktuálního uspořádání atomů. Potenciální energie může být modelována nejjednoduššeji Coulombovskou interakcí (látky z iontovou vazbou) nebo popsána vhodným potenciálem (Buckingham, Leonard-Jones nebo Born-Mayer) za předpokladu, že vhodné parametry potenciálu jsou známé pro daný problém [22]. Pro většinu intermetalických látek stačí popis meziatomové interakce pouze pomocí její repulsivní části – minimální meziatomové vzdálenosti (anti-bump); každý strukturní model obsahující příliš krátké meziatomové vzdálenosti je penalizován vysokou hodnotou této CF. Výpočty ab-initio krystalové energie jsou ve většině případů příliš časově náročné pro jejich použití v globální optimalizaci. Energie krystalové mříže jako součást CF je používaná ve výpočetních programech [23-26], anti-bump CF jsou pak k dizpozici téměř ve všech programech.

Aktuální strukturní model se skládá z jednotlivých strukturních bloků: izolovaných atomů, molekulárních fragmentů, celých molekul, koordinačních mnohostěnů aj. Je výhodné použít jednotný popis strukturních bloků pomocí vnitřních souřadnic (stereochemical descriptors) jako vazebné vzdalenosti, vazebné úhly a torzní úhly. Polohu a orientaci celého bloku pak pomoci tří krystalografických souřadnic (popisujících polohu těžiště anebo jednoduššeji polohu vybraného atomu) a tří úhlů (např. Eulerových). Výhody jsou hned dvojí: nižší počet volných parametrů N (pro popis koordinačního čtyřstěnu potřebujeme 5´3=15 krystalografických souřadnic jednotlivých atomů, ale jenom 3+3=6 polohových a orientačních souřadnic bloku) a jejich přímý fyzikálně-chemický význam umožňující vložení jejich správných hodnot do strukturního modelu. Hodnoty vnitřních souřadnic mohou být buď pevné (rigid body) anebo proměnné v předem odhadnutelném (např. ze znalosti struktur příbuzných krystalů) a většinou úzkém (ne však pro torzní úhly v molekulách) intervalu. Vnitřní souřadnice bloků mohou být obdrženy z kartezských souřadnic daného bloku [27] nebo uloženy v tzv. Z-maticích (http://chemistry.umeche.maine.edu/Modeling/GGZmat.html).

Algoritmus globální optimalizace

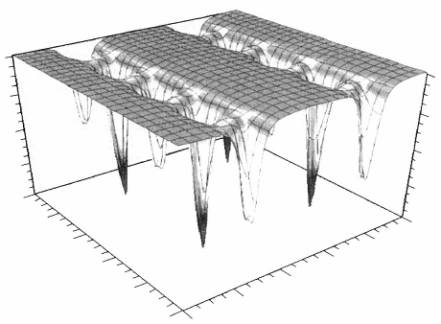
Úkolem algoritmu je najít globální minimum celkové CF, kterou si můžeme představit jako hyperplochu v N-rozměrném prostoru (N parametrů, které určujeme). Příklad dvojrozměrného řezu takovou hyperplochou je znázorněn na obr. 2.

Obr. 2: Dvojrozměrný řez 12-rozměrnou hyperplochou c² famotidinu B ; převzato z [1].

Jak je vidět, hyperplocha CF obsahuje řadu lokálních minim a algoritmus musí být schopen najít minimum globální (odpovídající spravnému strukturnímu modelu), ale i být schopen uniknout z minima lokálního. Je vidět, že jakýkoli algoritmus kontrolovaný pouze gradientem hyperplochy (např. metoda nejmenčích čtverců) skončí dříve či později v lokálním minimu. Je to typický problém globální optimalizace a krystalografie zde našla řadu inspiraci v ostatních vědách jako teoretická fyzika, sociologie (modelování složitých společenských systemů) či ekonomie (předpovídání ekonomických vývojů). Pro více informací o globální optimalizaci lze doporučit [28]. Je nutné zdůraznit, že každý algoritmus globální optimalizace je výpočetně nesmírně náročný. První příklady řešení struktur globální optimalizace strukturního modelu jsou spojeny s předpovídáním existence nových látek na základě minimalizace krystalové energie a prášková difrakční data byla užívána spíše pro kontrolu správnosti modelu a posteriori [29, 30].

1. Trial-and-error, grid search

První práce řešení struktur globální optimalizací s difrakčními daty užívaly jednoduše metodu zkoušky a omylu (trial-and-error) [31], která se, zjednodušeně řečeno, vyvinula v systematické prohledávání objemu elementární buňky [32, 33]. Oba přístupy však brzy narazily na hranice svých možností a bylo jasné, že je musí nahradit “inteligentnější“ algoritmy.

2. Monte Carlo - simulované žíhání

Termín “Monte Carlo“ je v literatuře rezervován pro metodu vzorkování určitého prostoru parametrů (hyperplochy) pomocí náhodných kroků zajištujících ergodicitu vzorkování, t.j. každý bod hyperplochy může být dosažen se stejnou pravděpodobností. Je to globální vzorkování nikoliv optimalizace. Teprve při užití určité “inteligence“, jako např. simulované žíhání se algoritmus stává globální optimalizací. Simulované žíhání se nejčastějí provádí pomocí Metropolisova algoritmu [34] navrženého při simulaci chování soustavy pevných koulí - plynu. Schema algoritmu je na obr. 3.

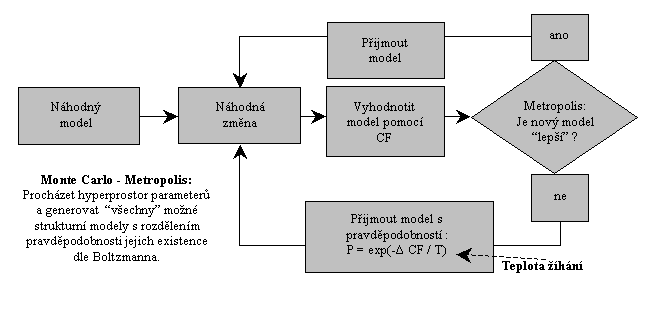
Obr. 3: Schema Monte-Carlo optimalizace s Metropolisovým algoritmem.

Pravděpodobnost přijmutí “horšího“ modelu stoupá se teplotou žíhání T a zajišťuje, že algoritmus nezůstane během svého optimalizovaného vzorkování uvězněn v lokálním minimu hyperplochy CF. Optimalizace začíná s vysokou teplotou T a s ní i spojenými velkými náhodnými změnami modelu (změny N volných parametrů). To zajišťuje rychlé avšak hrubé vzorkování hyperplochy. V dalších krocích algoritmu se teplota postupně snižuje s cílem jemněji vzorkovat hyperplochu v okolí již globálního minima, kam algoritmus mělo zavést žíhání při vyšší teplotě. Odtud název algoritmu. První užití Monte Carlo optimalizace pro řešení struktur z práškových difrakčních dat [35] užívalo žíhání při konstantní teplotě T. Simulované žíhání s různými způsoby kontroly postupného snižování teploty T je v současné době nejrozšířenější metoda globální optimalizace aplikovaná na řešení struktur z práškových dat [23-25, 36-41]. Při aplikování simulovaného žíhání je nutno správně odhadnout rychlost “chlazení“, která závisí na počtu volných parametrů N a také na kvalitě dat. Velká rychlost vede k “zakalení“ vysokoteplotního modelu (systém zůstane v lokálním minimu), nízká rychlost vede ke neúměrně dlouhým časům optimalizace (je nutno říci, že ne každý běh algoritmu vede do globálního minima; je to přece jenom algoritmus založený na náhodnosti). Proto byla v [42] navržena alternativa algoritmu známá jako paralelní žíhání, které probíhá souběžně při několika teplotách T_i rozdělěných mezi nejnižší a nejvyšší vhodnou teplotu a algoritmus pravidelně porovnává nejlepší řešení (strukturní modely) v sousedních (vzhledem k teplotě) optimalizacích pomocí např. opět Metropolisova algoritmu. Tím je zajištěna přítomnost všech teplot žíhání v každém okamžiku optimalizace a parametry algoritmu jsou tak nezávislé na problému i datech. Velikost náhodných změn strukturního modelu je větší pro vyšší teploty a může být automaticky kontrolována např. předem daným pevným poměrem mezi přijatými “lepšími“ a “horšími“ modely v Metropolisově algoritmu (obr. 3).

Někdy se v krystalografické literatuře setkáme s pojmem “Reverse Monte Carlo“, který je užíván některými autory [43] pro aplikaci tohoto optimalizačního algoritmu na neuspřádané struktury a kapaliny (modelování Pair Distribution Function), ale i na krystalické látky [40].

3. Vývojové teorie - genetický algoritmus

Genetický algoritmus je založen na Darwinově evoluční teorii. Pro historii jeho využití v globální optimalizaci odkazujeme čtenáře na [44], jeho schema je znázorněno na obr. 4.

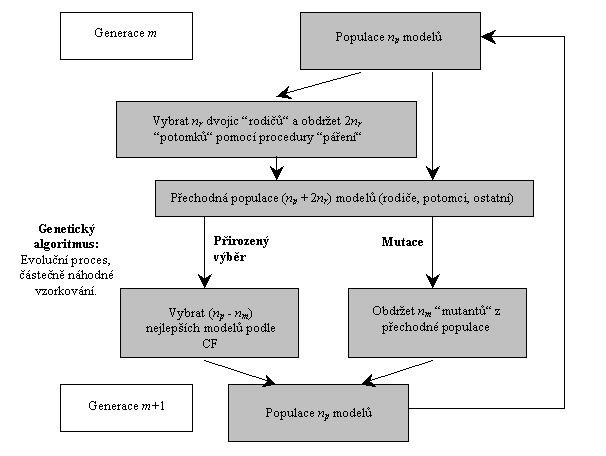
Obr. 4: Schema genetického algoritmu .

Každý strukturní model z aktuální populace n_p modelů je popsán svým “chromozomem“, který je souborem “genů“ – strukturních parametrů, které určujeme. Charakteristickou každého modelu – jedince je jeho vhodnost (fitness), popsána opět jednou CF nebo kombinací více CF. Aplikováním genetických operátorů, “páření“ (kombinace genů obou “rodičů“) a náhodné “mutace“, jsou vytvářeni noví jedinci a jejich vhodnost je testována. Dle Darwinova principu o přežití “nejlepších“ jedinců jsou formovány nové a nové generace; populace se vyvíjí směrem ke globálnímu minimu hyperplochy CF. Tak jako v simulovaném žíhání jsou kontrolnímí parametry algoritmu žíhací teplota a velikost náhodných změn modelu, jsou v genetickém algoritmu těmito parametry podíl a typ mutace na změně jedné generace, způsob výběru “rodičů“ a typ jejich “páření“ a velikost populace. Podíl mutace musí být dost výrazný, aby se zamezilo “degeneraci“ genetického fondu (uvěznění v lokálním mimimu), způsob výběru “rodičů“ může být např. “elitistický“. Genetický algoritmus jako metodu globální optimalizace aplikovanou na řešení struktur z práškových dat lze najít např. v [45, 46]. Jeho verze dle Lamarkianovy evoluční teorie [47] aplikuje také “vývoj“ jedince během jeho “života“ pomocí lokální minimalizace (posun jedince k nejbližšímu lokálnímu minimu hyperplochy CF).

4. Další algoritmy

Řada dalších algoritmů byla testována v globální optimalizaci aplikované na řešení struktur z práškových dat. Jmenujme zde pouze algoritmus založený na sociálním chování hejna jedinců, “swarm“, aplikovaný v [48] a velmi slibný hybridní Monte Carlo algoritmus, aplikovaný v [49], který kombinuje výhody Monte Carlo vzorkování hyperplochy CF s efektivností lokalizace jejích minim pomocí formalismu molekulární dynamiky.

Který algoritmus je nejlepší? Přímá odpověď neexistuje neboť srovnání není jednoduché a závisí ve velké míře na problému, na který globální optimalizaci aplikujeme. Simulované žíhání má však velkou výhodu oproti genetickému algoritmu v menším počtu kontrolních parametrů algoritmu a může být proto snadněji naprogramován (zvlástě ve své podobě paralelního žíhání) jako “black-box“ algoritmus. Řada pokusů byla také učiněna o kombinaci výhod obou algoritmů v jeden hybridní [50].

Jak pomoci globální optimalizaci?

Pravděpodobnost nalezení globálního minima lze zvýšit omezením objemu elementární buňky, kterou musí algoritmus vzorkovat (to odpovídá zjednodušení tvaru hyperplochy CF). Lze použít např. informaci o molekulárních obálkách, metodu známou z krystalografie proteinů (kde prášková difrakce našla řadu inspirací, protože se potýká se stejným problémem, nízký poměr počtu dat k volným parametrům). Molekulární obálky jsou vlastně Fourierovy mapy s velmi nízkým rozlišením (periodické nodální plochy), zpočtené z několika nízkoúhlových dobře rozlišených reflexí. Iso-plochy v takovéto mapě od sebe oddělují oblasti s vyšší (polohy atomů) a nízkou (prázdné oblasti) elektronovou hustotou. Algoritmus globální optimalizace pak prohledává jen ty první. Aplikaci lze najít v [51].

Na začátku optimalizace je strukturní model mnohem více vzdálen od pravdivého řešení než když se algoritmus blíží globálnímu minimu. Tuto informaci lze do algoritmu vložit pomoci pravděpodobnosti (likelihood), že takový model bude odpovídat pozorovaným difrakčním (či jiným) datům. Hrubě řečeno modifikujeme algoritmus tak, aby byl více “tolerantní“ ke špatným modelům a nebral je příliž “vážně“. Myšlenku lze rozšířit tak, že produkujeme úmyslně špatný model tím, že je jenom částečný (vynecháme např. molekulu rozpouštědla). Takový model je pak menší (méně volných parametrů) a hyperplocha CF jednodušší. Chybějící část modelu (blur) a její příspěvek do difrakce však musí být správně popsán, právě pomocí maximum likelihood formalismu. Aplikaci lze najít v [52].

Poslední příspěvek, výpočetní program FOCUS, vlastně nepatří do metod globální optimalizace strukturního modelu, ale zařazujeme ho zde, protože využívá také “inteligentní“ vzorkování přímého prostoru (elementární buňky). Je to metoda, která pracuje s integrálními intensitami obdrženými s práškového difrakčního záznamu a používá dodatečnou chemickou informaci (znalost typických topologií, atomových koordinací, příbuzných krystalových struktur) pro interpretaci a vzorkování Fourierových map elektronových hustot. Při nalezení “slibného“ fragmentu v mapě je celý cyklus opakován s fázemi reflexí obdrženými z tohoto částečného strukturního modelu až do identifikace modelu schopného již vypřesňování. Aplikaci na krystalografii zeolitů lze najít v [53].

Závěr

Zde končí etapa řešení strukury, na kterou navazuje vypřesnění struktury prováděné dnes téměř výhradně pomocí Rietveldovy metody a analýzy Fourierových map. Jak je vidět z obr. 1 neexistuje jediná “zlatá“ cesta v bludišti řešení krystalových struktur pomocí práškové difrakce. Výkonnost metod pracujících v reciprokém a v přímém prostoru je dnes srovnatelná jak pro molekulární krystaly, tak i pro látky neobsahující jasně definované molekuly (extended crystals, inorganické látky). Větší úspěšnost jedné nebo druhé metody je silně podmíněna daným problémem. Vývoj obou typů metod stále intenzivně pokračuje, je zajímavé podotknout, že úspěch globální optimalizace není dán jenom vzrůstem výpočetní výkonnosti, ale ve velké míře i vývojem lepších algoritmů.

Ve spěchu aplikace dnešních výkonných metod práškové difrakce je však nutno nezapomenout na první kroky v bludišti obr. 1, vzorek a měření dat. Více času stráveného na syntéze naší látky produkující vzorek bez příměsí a s užšími difrakčními liniemi jakož i na optimalizaci difrakčního experimentu se nám bohatě vrátí ve snazší analyze dat. Staré přísloví stále platí: “práce kvapná, málo platná“.

Odkazy

[1] David W.I.F, Shankland K., McCusker L.B. & Baerlocher Ch., Editors; Structure Determination from Powder Diffraction Data, IUCr. Monographs on Crystallography 13, Oxford University Press, 2002

[2] Visser, J.; J. Appl. Crystallogr. 2 (1969) 89-95

[3] Boultif, A. & Loüer, D.; J. Appl. Crystallogr. 24 (1991) 987-993

[4] Werner, P.-E., Eriksson, L. & Westdahl, M. ; J. Appl. Crystallogr. 18 (1985) 108-113

[5] Rietveld, H.M.; J. Appl. Crystallogr. 2 (1969) 65-71

[6] Le Bail, A.; Accuracy in Powder Diffraction II, Proceedings of the International Conference, May 26-29, 1992 NIST Special Publication 846, E. Prince and J.K. Stalick, Editors page 213.

Také: http://www.cristal.org/iniref/lbmeth.html

[7] Pawley, G.S.; J. Appl. Crystallogr. 14 (1981) 357-361

[8] Markvardsen, A., David, W.I.F., Johnson, J.C. & Shankland, K.; Acta Crystallogr. A57 (2001) 47-54

[9] Altomare, A., Foadi, J., Giacovazzo, C., Guagliardi, A. & Moliterni, A.G.G.; J. Appl. Crystallogr. 29 (1996) 674-681

Také: http://www.irmec.ba.cnr.it/

[10] Jansen, J., Peschar, R. & Schenk, H. ; J. Appl. Crystallogr. 25 (1992) 237-243

[11] David, W.I.F.; J. Appl. Crystallogr. 20 (1987) 316-319

[12] Estermann, M.A. & Gramlich, V.; J. Appl. Crystallogr. 26 (1993) 396-404

[13] Zachariasen, W.H. & Ellinger, F.H.; Acta Crystallogr. 16 (1963) 369-375

[14] Shankland, K., David, W.I.F. & Sivia, D.S.; J. Mater. Chem. 7(3) (1997) 569-572

Také: Brunelli, M., Wright, J.P., Vaughan, G.B.M., Mora, A.J. & Fitch, A.N.; Angew. Chem. Int. Ed. 42 (2003) 2029-2032

[15] Dahms, M. & Bunge, H.J.; Textures and Microstructures 6 (1986) 167-179

Také: Bunge, H.J., Dahms, M. & Brokmeier, H.G.; Cryst. Rev. 2 (1989) 67-88

Také: Hedel, R., Bunge, H.J. & Reck, G.; Textures and Microstructures 29 (1997) 103-126

[16] Wessels, T., Baerlocher, Ch., McCusker, L.B. & Creyghton, E.J.; J. Am. Chem. Soc. 121 (1999) 6242-6247

Také: Wessels, T., Baerlocher, Ch. & McCusker, L.B.; Science 284 (1999) 477-479

Také: http://www.kristall.ethz.ch/LFK/research/zeolite_group/Texture/Texture.html

[17] Černý, R.; Advances in X-ray Analysis 40 (1998) CD-ROM

Také: Černý, R. Mat. Sci. Forum 321-324 (1999) 22-28

Také: Černý, R. Mat. Sci. Forum 378-381 (2001) 24-29

Také: http://crystsun1.unige.ch/cerny/rcerny.htm

[18] Rius, J.; Acta Crystallogr. A49 (1993) 406-409

[19] Bricogne, G.; Acta Crystallogr. A47 (1991) 803-829

[20] Gilmore, C.J. & Nicholson, W. ; Trans. Amer. Cryst. Association. 30 (1994) 15-27 Také: http://www.chem.gla.ac.uk/staff/chris/powder.htm

[21] Shankland, K., David, W.I.F. & Csoka, T.; Z. Kristallogr. 212 (1997) 550-552

[22] GULP(General Utility Lattice Program)

Také: http://www.ch.ic.ac.uk/gale/Research/gulp.html

[23] Engel G.E., Wilke S., Knig O., Harris K.D.M. & Leusen F.J.J.; J. Appl. Cryst. 32 (1999) 1169-1179

Také: http://www.accelrys.com/cerius2/powder.html

[24] TOPAS User’s Manual, Bruker AXS GmbH, 2000

Také: Coelho, A.A.; J. Appl. Cryst. 33 (2000) 899-908

[25] Putz H., Schön J.C. & Jansen M.; J. Appl. Cryst. 32 (1999) 864-870

Také: http://www.crystalimpact.com/endeavour/

[26] Kariuki B.M., Serrano-Gonzáles H., Johnston R.L. & Harris K.D.M.; Chem. Phys. Lett. 280 (1997) 189-195

[27] Andreev Y.G., Lighfoot, P. & Bruce P.G.; J. Appl. Cryst. 30 (1997) 294-305

[28] Floudas, C.A.; Deterministic Global Optimization: Theory, Algorithms and Applications, Kluwer, Dordrecht 1999.

Také: http://www.princeton.edu/~chemical/faculty/floudas/floudas.html

[29] Catlow, C.R.A., Cormack, A.N. & Theobald, F. ; Acta Crystallogr. B40 (1984) 195-200

[30] Deem, M.W. & Newsam, J.M.; Nature 342 (1989) 260-262

[31] Taylor, J.C. & Wilson, P.W.; Acta Crystallogr. B30 (1974) 2664-2667

[32] Chernyshev, V.V. & Schenk, H.; Z. Kristallogr. 213 (1998) L1-L3

[33] Masciocchi, N., Bianchi, R., Cairati, P., Mezza, G., Pulati, T. & Sironi, A.; J. Appl. Cryst. 27 (1994) 426-429

[34] N. Metropolis, A.W. Rosenbluth, M.N. Rosenbluth, A.H. Teller and E. Teller: J.Chem. Phys. 21 (1953) 1087-1092

[35] Harris, K.D.M., Tremayne, M., Lightfoot, P. & Bruce, P.G.; J. Am. Chem. Soc. 116 (1994) 3543-3547

[36] Andreev Y.G., MacGlashan G.S. & Bruce P.G.; Phys. Rev B, Cond. Matter 55 (1997) 12011-12017

[37] David W.I.F., Shankland K. & Shankland N.; J. Chem Soc. Chem. Commun. 8 (1998) 931-932

Také: http://www.ccdc.cam.ac.uk/prods/dash/#ref1

[38] Pagola, S., Stephens, P.W., Bohle, D.S., Kosar, A.D. & Madsen, S.K.; Nature 404 (2000) 307-310

Také: http://powder.physics.sunysb.edu/programPSSP/pssp.html

[39] Favre-Nicolin, V. & Černý, R.; J. Appl. Cryst. 35 (2002) 734-743

Také: http://objcryst.sourceforge.net/

[40] Le Bail, A; Materials Science Forum 378-381(2001) 65-70

Také: http://www.cristal.org/sdpd/espoir/index.html

[41] Toraya, H. & Yamazaki, S.; Acta Crystallogr. B58 (2002) 613-621

[42] Falcioni M. & Deem. M.W.; J. Chem. Phys. 110 (1999) 1754-1766

Také: http://ccp14.semo.edu/ccp/web-mirrors/zefsa/zefsaII/

[43] Tucker, M.G., Dove, M.T. & Keen, D.A.; J. Appl. Cryst. 34 (2001) 630-638

Také: http://www.studsvik.uu.se/Software/rmc/rmcpow.htm

[44] Michalewicz, Z.; Genetic Algorithms + Data Structures = Evolution Programs,

3^rd edn., Springer-Verlag, Berlin 1996

[45] Shankland K., David W.I.F. & Csoka T.; Z. Kristallogr. 212 (1997) 550-552

[46] Kariuki B.M., Serrano-Gonzáles H., Johnston R.L. & Harris K.D.M.; Chem. Phys. Lett. 280 (1997) 189-195

Také: http://www.dur.ac.uk/j.m.hutson/ccp6-98/node36.html

[47] Turner, G.W., Tedesco, E., Harris, K.D.M., Johnston, R.L. & Kariuki, B.M.;

Chem. Phys. Letters 321 (2000) 183-190

[48] Csoka, T. & David, W.I.F.; Acta Crystallogr. A55 (1999) Supplement

[49] Johnston J. C., David W. I. F., Markvardsen A. J. and Shankland K.; Acta Cryst. A 58 (2002) 441-447

[50] http://www.densis.fee.unicamp.br/~moscato/memetic_home.html

Také: http://bruce.edmonds.name/aigp/

[51] Brenner S., McCusker L. B. & Baerlocher Ch.; J. Appl. Cryst. 35 (2002) 243-252

Také:http://www.kristall.ethz.ch/LFK/research/zeolite_group/PNS/Structure_Envelopes.html

[52] Markvardsen A.J, David W.I.F. & Shankland K.; Acta Cryst. A58 (2002) 316 – 326

[53] Grosse-Kunstleve R.W., McCusker L.B. & Baerlocher Ch.; J. Appl. Cryst. 30 (1997) 985-995

Také: http://www.kristall.ethz.ch/LFK/research/zeolite_group/FOCUS/FOCUS.html