DECONVOLUTION METHODS

M. Čerňanský

Department of Metal Physics,

Institute of Physics, Academy of Sciences of the Czech Republic

Na Slovance 2, 182 21 Prague 8, Czech Republic

Introduction

Profiles of diffraction lines contain important information about the real structure of polycrystalline materials, e.g. about crystallite size and lattice strains. However, the physical interpretation is related to pure or physical diffraction profiles f, which in most cases cannot be measured directly and are obtained from really measured profiles h by removing the instrumental distortion described by the instrumental function g. This function includes both geometrical factors (finite width of source and slits, divergence of beams, flat-specimen surface, its transparency and displacement, imperfect focussing, etc.) and spectral factors (e.g. the finite wavelength interval of the primary radiation). The instrumental function g is obtained in practice by the measurement of a suitable standard without diffraction broadening. The function f, g, h are connected by the convolution relation

(1)

denoted usually as h=f*g. The solution of the integral equation (1) for the unknown function f is called deconvolution. Equation (1) is the special type of the more general relation

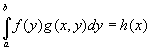(2)

which is the Fredholm integral equation of the first kind for an unknown function f with the kernel g(x,y). Equations (1) and (2) can be most generally expressed in the operator form

(3)

In our case it is necessary to determine the unknown f from the known A and h. This is contrary to the direct problem of estimating h from the known A and f. Our case belongs thus to the category of inverse problems which are often ill-posed, incorrect - the existence, unambiguity and stability of the solution are not a priori warranted. Stability means that small changes in input data lead to small changes in calculated results. In practice, functions entering the calculations are usually not expressed analytically but by discrete sequences of values in intervals of limited length. Each term of these sequences is known with a certain experimental accuracy and, furthermore, rounding errors arise during calculations. Unfortunately, the stability of the problems described by equations (1) and (2) is very problematic.

Considering the above-mentioned problems of stability of the solution, the success in the restoration of the physical profile is strongly dependent on the quality of the input data and on their preprocessing, including the background subtraction, smoothing, sampling and interpolation. It is necessary, first, to eliminate data containing discontinuities and truncations leading to false details.

Deconvolution methods

Method of the system of linear algebraic equations

Practical computations led naturally to discretized forms of equations (1) and (2). The integral was replaced by the sum, and continuous functions were sampled in discrete points. Integral equation (2) was thus replaced by the system of linear algebraic equations

(4)

where , , . Values , appearing in the discretized form of the convolution (1), depend only on the difference of indices j-i. denotes weight factors, depending on the quadrature formula, which can be easily included in matrix elements of the system (4). The noise is a very important factor.

It has been revealed that the efforts to replace the integral by the sum by decreasing the step of variables x, y and by increasing the number of equations in system (4) leads to unphysical, unfounded oscillations. A greater step and lower dimension of the matrix gave paradoxically better results and a smoother solution. Increased difficulties have appeared for a small ratio of widths of functions h and g and for input data with an increased fraction of noise. The higher dimension of the matrix of system (4) meant a stronger amplification of the noise in the process of matrix inversion . It has been recommended that data be smoothed before computations, and a suitable number of equations preserving useful information on one hand and non-generating instability on the other hand be choosen. Iterative methods were recommended to solve system (4). The mentioned problems were closely connected with the ill-conditioned nature of equations (1) and (2) and with the requirement to consider the noise. The system (4) can be solved by the method of Lagrange multipliers, the least-squares method, using pseudo-inverse matrix and the singular value decomposition.

Method of inverse filtering

This method of deconvolution is based on Borel's convolution theorem:

Fourier transform of the convolution h = f*g is equal to the product of Fourier transforms of functions f and g, respectively

(5)

Multiplication of equation (5) by the (ideal) inverse filter 1/G(ω) and performing the inverse Fourier transform leads to the solution f.

The inverse filtering described by equation (5) belongs to methods amplifying the random noise. It is now necessary to modify the method to minimize the influence of noise.

Real instruments have a defined pass band characterized by the frequency : for . The first way of suppressing the noise is to narrow the interval of frequencies to , where . However, the narrowing of the frequency interval can result in a sudden fall of F (ω) to zero for . This truncation causes oscillations and other false details in the solution f(x). This fact induces the introduction of spectral windows ensuring a continuous transition of to zero for . Another way to suppress the noise is the application of a spectral window directly to the entire interval .

The above-mentioned modifications of the method of inverse filtering led to neglecting the noise instead of its computation. The drawback lies in the subjectivity of the choice of a spectral window and in the fact that these windows do not respect the processed data. Consequently, the Wiener optimal filter [1] is often used in deconvolution by the method of inverse filtering, for which this filter is extremely important.

Iterative method of the integral equation

Equation (1) can be transformed to the Fredholm integral equation of the second kind

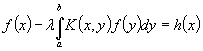(6)

In the case of deconvolution, and , (δ is the Dirac delta function). One of the standard procedures of solving equation (6) is the method of successive approximations. These iterations for equation (1) - deconvolution - have the form

(7)

where , .

This method is more widely applied and more attractive since the deconvolution is calculated by means of convolutions. However, it follows from eq. (7) that the higher the iteration, the more appreciable the influence of errors owing to the factor n in the n-th iteration. Thus, there exists an optimal number of iterations and, furthermore, iterations with rapid convergence are desirable. The convergence of iterations can be improved by the relaxation parameter.

First, the iterative methods are very popular because of the possibility of terminating an iterative process when the noise is too strongly amplified. Second, it is possible to introduce constraints on the solution. Therefore, new modifications of iterative methods have appeared. Especially, the iterative ratio algorithm is often used.

Method of regularization

The starting point for regularization is the addition of prior information on the solution, e. g. on its smoothness, deviations of the right-hand side or also on the inaccuracy of the operator A, etc. The goal of the regularization is to obtain an approximate but stable solution. The way to realize it is to solve another correct problem. In the case of Tikhonov regularization [2], it is minimization of the functional

(8)

where the residuum (discrepancy)

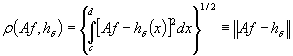(9)

refers to the original problem. The second term, the stabilizer , has a smoothing or stabilizing effect on the solution. It often has the form

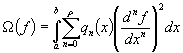(10)

where are given non-negative functions. The limit of summation p indicates the order of the stabilizer and, equally, the order of regularization. The non-negative number is the regularization parameter controlling the smoothness of the regularized solution. Function minimizing may be found by solving the corresponding Euler equation or by some gradient method.

Method of maximum entropy

The entropy for the discrete random variable is defined by the relation

(11)

where is the probability that . Following the principle of maximum entropy, one can state that from all possible functions one is realized for which H(x) has the maximum, and possibly satifies further conditions. Application of the principle of maximum entropy to the restoration of objects from measured data is based on the idea that the object, the physical profile f (and the noise), may be regarded as the probability function. Entropy in that case is the measure of quality of the restored object, especially in the sense of the smoothness. Smoother curves have higher entropy. The fact that physical profile f may be considered to be the probability function p in equation (11) follows from the statistical model of its formation.

The usual procedures present the following solution of the mentioned optimization problem - the maximization of the entropy

(12)

The parameter (signal-to-noise uncertainty) may be defined if the inequality is assumed. This parameter allows the assigning of different weights to the smoothing of f and N. Higher means higher weight of the maximization of the entropy of noise, and consequently, its better smoothing. Lagrange multipliers and μ may be estimated from the equations

(13)

(14)

Eq. (13) is the discretized form of eq. (2) with respect to noise. The non-negative constant B enables to define the logarithm in the entropy of noise N(x_m). Eq. (14) describes the integral intensity of the physical profile f.

Method of maximum likelihood

This method in mathematical statistics is usually related to the following problem. The probability density function is given of the random variable x with a known functional form and unknown parameters . A random sample of observed values of the random variable x is chosen as the result of n trials. This random sample serves to estimate parameters . The likelihood function L is defined by the relation

(15)

L is evidently the probability of obtaining the sampling set . Estimates of are performed for values maximizing L or lnL, expressing the experience that more probable phenomena occur more frequently. In the classical procedure, the following system of equations is solved

(16)

The application of the method of maximum likelihood to the solution of the Fredholm integral equation of the first kind lies in considering the unknown parameters to be values of an unknown physical profile f. The measured profile h is regarded as the probability density function, the parameters of which are to be estimated.

Bayesian methods

The joint probability of some events, f and h, can evidently be expressed in two ways by the conditional probability [3]

(17)

The well known Bayes rule follows from (17)

(18)

The quantities f, h and also n are denoted in equation (18) as random vectors which occur in the discrete problem of restoration of the object, i.e. the physical profile f. More precisely, the quantities p are probability density functions.

The prior probability density p(f) contains preliminary information about the vector f before the data h have been taken. The vector h is the result of a measurement; it depends on the vector f in the experiment. This dependence is known: h = Gf + n, and is described by a conditional probability density

(19)

The searched posterior probability density p(f | h) gives more precise information about f corresponding to the results of the measurement of h. The Bayes estimate is defined

(20)

which is the mean of f conditioned on the observed vector h. The calculation of p(f|h) assumes that the prior probability densities on the right-hand side of equation (18) are known. Defining these quantities is a general problem of Bayesian estimates. Prior probability density functions on the right-hand side of equation (18) need not be known in Bayesian-based iterative methods of restoration.

Concluding remark

The above-mentioned deconvolution methods belong to the so-called direct deconvolution of diffraction profiles. The overview of these methods is given in [4]. The other approach is based on the convolution of physical and instrumental profiles in which the physical profile is approximated by a function of a limited number of parameters, which follow from the microstructure model. The lucid example of the combination of the both approaches is given in [5].

[1] W.H. Press, S.A. Teukolsky, W.T.Vetterling & B.P. Flannery : Numerical Recipies in C.

Cambridge 1995. Cambridge University Press.

[2] A.N. Tikhonov & V.Ya. Arsenin : Methods for the Solution of Incorrect Problems. Moscow

1986. Nauka (3^rd ed. in Russian). [English translation New York 1977. Wiley].

[3] A. Rosenfeld & A.C. Kak : Digital Picture Processing. Orlando, Florida 1982. Academic Press.

[4] M. Čerňanský : Restoration and preprocessing of physical profiles from measured data.

in R.L. Snyder, J. Fiala & H.J. Bunge (eds.) Defect and Microstructure Analysis by

Diffraction. Oxford 1999. IUCr/Oxford University Press.

[5] D. Rafaja : Materials Structure 7 (2000) 43-50.