COMBINATION OF MODELING AND EXPERIMENT IN ANALYSIS OF PARTIALLY DISORDERED STRUCTURES.

Pavla Čapková¹, Jaroslava Repáková¹, Bohdan Koudelka¹, Miroslav Pospíšil¹, Miroslava Trchová², Zdeněk Weiss³, Vítězslav Zima² and Michal Ilavský²

¹Faculty of Mathematics and Physics Charles University Prague, Ke Karlovu 3, CZ-12116 Prague, Czech Republic; E-mail: capkova@karlov.mff.cuni.cz ; ²Institute of Macromolecular Chemistry, Academy of Sciences of the Czech Republic, 16206 Prague 6, Czech republic; ³Technical University Ostrava, 70833 Ostrava, Czech Republic;

Abstract:

Strategy of structure analysis for partially disordered crystal structures has been worked out, based on combination of modeling (i.e. force field calculations) and experiment (diffraction methods and vibration spectroscopy). Modeling in conjunction with experiment enables us to analyze the disordered structures, where the conventional diffraction analysis fails. Experiment plays a key role in modeling strategy and in corroboration of modeling results. X-ray powder diffraction and IR spectroscopy were found as very useful complementary experiments to molecular modeling. Molecular mechanics and molecular dynamics simulations were carried out in Cerius²/Materials Studio modeling environment. An overview of structures solved by this method will be presented, especially intercalates, liquid crystals and liquid crystalline polymers.

Introduction

Intercalates, liquid crystals and liquid crystalline polymers belong to partially disordered structures, where the disorder obstructs the conventional structure analysis based on diffraction method only. Due to the disorder it is also impossible to prepare the single crystals of reasonable size for the diffraction measurements and powder diffraction pattern is in addition to the disorder affected by the preferred orientation of crystallites. In such a case molecular modeling i.e. molecular mechanics and molecular dynamics represent very powerful tool in structure analysis of these systems. Molecular mechanics is a method of optimization of the structure and bonding geometry by energy minimization, where the energy is described by an empirical force field [1]. These force field calculations enable us to determine the structure of supramolecular systems, which are too large for ab-initio quantum chemical calculations and which exhibit certain degree of disorder and consequently the diffraction analysis fails in structure determination. Molecular dynamics simulations introduce the control of temperature and pressure to the system and enable us to study the dynamic processes like diffusion and phase transitions. Classical molecular dynamics involves the calculation of the time dependent movement of each atom in a molecule [1,2]. This is achieved by solving Newton's equations of motion. The temperature and the distribution of atomic velocities in a system are related through the Maxwell-Boltzmann equation [1,2].

Strategy of modeling

The strategy of modeling (i.e. the building of the initial models, the set up of energy expression, the choice and test of the force field, the definition of rigid fragments, the set up of fixed and variable structure parameters etc.) should be based on the available experimental data. X-ray powder diffraction a vibration spectroscopy has been found as very convenient complementary experiments to the molecular modeling. Comparison of x-ray powder diffraction patterns and IR/Raman spectra for the host structure, guest compound and intercalate reveals the changes of the host structure and guest species during intercalation and help to create the modeling strategy [3].

All the computational methods searching for the global energy minimum have to generate a large number of initial models using three different ways [4]: (1) Deterministic method for generation of starting models, performing the systematic grid search that covers all areas of the potential energy surface; (2) Molecular dynamics generating the starting geometry; (3) Stochastic methods /Monte Carlo, Genetic Algorithm/. In modeling of intercalated structures we used first two methods: the grid search using program SUPRAMOL [4] with the final energy minimization in Cerius² and molecular dynamics in Cerius² [5]. The first method, performing the systematic grid search can be used easily to generate starting models in case of small organic guest molecules or almost rigid large guests and rigid host layers. On the other hand molecular dynamics is very convenient method for generation of starting models in case of large flexible organic guest molecules.

As a result of molecular modeling we can get the structure model, the energy characteristics (energy of intermolecular interactions and charge distribution) and disorder characteristics (the type and degree of the disorder). Molecular simulations enable the prediction of structure and properties and thus represent big challenge for the design of new materials with desirable properties. All results presented in this paper were obtained using Cerius²/Materials Studio modeling environment from (MSI/Accelrys) [5].

Intercalated layered structures

Intercalation means an insertion of a guest molecule or ion into a suitable crystal structure without major rearrangement of the solid host structure [6,7]. Intercalation requires that the host structure has a strong covalent network of atoms, which remains unchanged on the intercalation reaction and that there are vacant sites in the structure. These vacant sites should be interconnected and of suitable sites to permit the diffusion of the guest species into the host structure. Layered crystal structures satisfy these requirements very well being able to accommodate very large guest molecules in the interlayer space by the free adjustment of the interlayer separations. A strong intralayer and weak interlayer bonding characterizes layered structures. A survey of different types of layered host structures and discussion of intercalation reactions for neutral and charged layers is given in [6,7]. Intercalation provides new routes for the synthesis of materials with controlled changes in the chemical and physical properties.

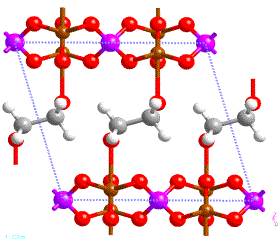
Figure 1:

High temperature phase of vanadyl

phosphate intercalated with dioxane

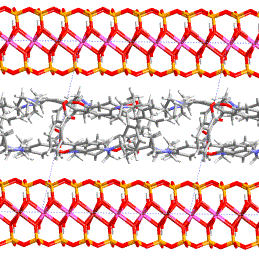
Figure 2: One example of intercalated layered silicates; [8] Montmorillonite intercalated with rhodamine B. Anchoring of dye molecules on silicates layers changes their optical activity, (absorption spectra, photoluminiscence etc. ). The way of guest anchoring to the host layer, the conformation changes, the arrangement of guest molecules in the interlayer space (monomers, dimers and higher aggregates) represent crucial parameters for optical properties of the intercalate.

These properties can be tuned by the proper choice of the host-guest combination, by the guest concentration and by co-intercalation of further guest species. This allows creating a large variety of structures for a wide scale of practical use. Intercalates can be used as adsorbents, catalysts, pharmaceutical products, chemical sensors, ionic conductors and various kind of electrochemical and opto-electronical devices [7].

Intercalation is in fact an insertion of a known molecule into a known crystal structure, consequently the structure analysis of intercalates has to solve specific problems. That means: to find the positions, orientation and ordering of the guest molecules in the host structure, to find the way of layer stacking, conformational changes of guest molecules in the interlayer space of the host structure and to characterize a possible disorder in guest arrangement and consequently in the layer stacking.

Combination of modeling with X-ray and synchrotron powder diffraction and with IR/Raman spectroscopy has been used to solve the structure of following series of intercalates: (1) layer silicates intercalated with organic and inorganic species (sorbents, catalysts, photo-function units), (2) graphite intercalated with transition metal chlorides (two-dimensional conductors), (3) tantalum sulfide intercalated with dye molecules (superconductors), and (4) vanadyl and zirconium phosphate intercalated with small organic molecules (catalysts, chemical sensors, proton conductors).

Structural phase transitions in liquid crystals and liquid crystalline polymers:

Liquid crystalline polymers can be obtained from specific monomers containing a mesogenic rigid segment. However the main trouble of processing such polymers is the high melting point, sometimes exceeding the decomposition temperature. To decrease the phase transition temperature, the flexible chain spacers between rigid mesogenic segments are inserted [9]. Each modification of monomers leads to the changes of thermal and mechanical properties of polymer systems and therefore the investigation of the structure and properties of monomers is important for understanding the of thermal and mechanical behaviour of derived polymer systems.

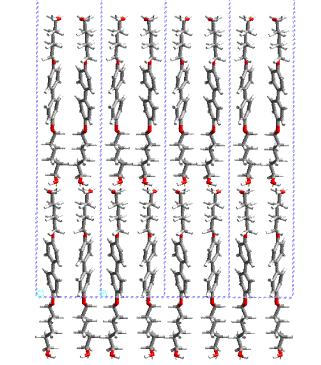
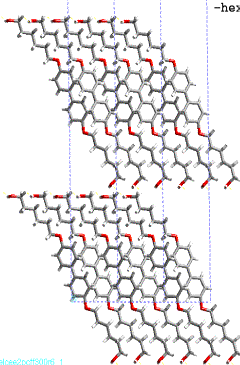
Phase transitions in molecular crystal of 4,4’- bis(6-hydroxy-1-hexyloxy)biphenyl have been studied using molecular dynamics simulations to reveal the mechanism of the phase transition into liquid crystalline state and to explain similar phase transition in polyuretane derived from this monomer. Figure 2a,b shows the layered crystal structure of 4,4’- bis(6-hydroxy-1-hexyloxy)biphenyl. In the figure 3 one can see the conformational changes of molecules as a result of molecular dynamic simulations carried out for room temperature, for 400 K in liquid crystalline state and for 500K above the melting point [11].

The design of new polymers with desirable thermal behavior requires the search for monomers with suitable combination of rigid mesogenic group and flexible chains. One way to this goal is the use of suitable side chains in flexible part of molecule. One example of this investigation is monomeric unit presented in the figure 5, which has been used with diisocyanate as a copolymer to design polyuretane with liquid crystalline behavior. Figure 6 shows the snapshots extracted from dynamic trajectory file at 300K at various time steps in dynamic trajectory, illustrating the rigidity of the polymeric chain in case of polyuretane.

Figure 3: Layered crystal structure of 4,4’- bis(6-hydroxy-1-hexyloxy)biphenyl; view along a and b axis.

The stiffness and rigidity of single polymer chain was described using two parameters, end to end distance and radius of gyration. The time dependence of these characteristics during dynamic simulations allows us to characterize the thermal and mechanical behavior of polyuretane. Characteristics obtained using dynamic simulation were in good agreement with results of experiment.

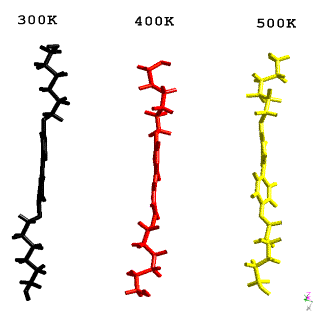
Figure 4:

Conformation of 4,4’- bis(6-hydroxy-1-hexyloxy)biphenyl molecule: at 300K, after the phase transition into liquid crystalline state at 400K, when the distortions of flexible chains result in disordered layer stacking in crystal structure in figure 2 and at 500K after the melting point, when the distortion of the rigid part of molecule leads to the melting of crystal structure.

Figure 5: The monomeric unit used together with diisocyanate for the design of polyuretan. (n = 6, X = Phenyl).

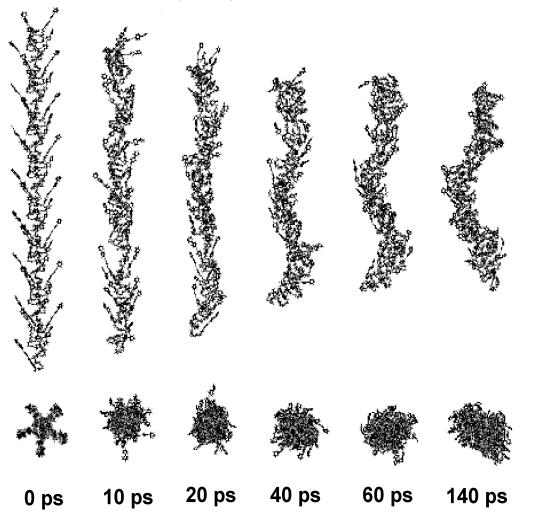
Figure 6: Snapshots extracted from dynamic trajectory at 300K, illustrating the degree of deformation and rigidity of the single polyuretane chain composed from diisocyanate and diol with side chain from the figure 5.

References:

[1] P. Comba, & T.W. Hambley (Ed.): Molecular Modeling. Weinheim, New York, 1995 VCH Verlagsgesellschaft mbH.

[2] D. Frenkel & B. Smit: Understanding Molecular Simulation. San Diego, New York, London, 1996, Academic Press.

[3] P. Čapková, M.Trchová, P. Hlídek, H. Schenk & M.Ilavský:, J. Molecular Structure, 559 (2001) 209-217.

[4] B. Koudelka & P. Čapková, J. Mol. Model, 8 (2002), 184-190.

[5] Cerius² documentation, June 2000, Molecular simulation/Accelrys, Inc. San Diego, USA

[6] A.J. Jacobson: Intercalation reaction of layered compounds. In: Solid state chemistry compounds, eds.: Cheetham A.K., Day P., Oxford (1992), Clarendon Press.

[7] A. Lerf: Intercalation Compounds in Layered Host Lattices: Supramolecular Chemistry in Nanodimensions. In: Handbook of Nanostructured Materials and Nanotechnology, vol. 5, eds.: Nalwa H.S, Academic Press, New York, (2000).

[8] M. Pospíšil, P. Čapková, H. Weissmannová, Z. Klika, M. Trchová, M. Chmielová & Z. Weiss, J. Mol. Model, 9 (2003) 39-46.

[9] M. Ilavský, K. Bouchal, H. Valentová, F. Lednický, A. Sikora & J. Baldrian J.: Macromol Sci. Phys. B37 (1998) 645-666.

[10] K. Goubitz, P. Čapková, K. Melánová, W. Molleman H. Schenk, Acta Cryst., B57 (2001) 178-183.

[11] P. Čapková, M. Trchová, P. Hlídek, H. Schenk, M. Ilavský: J. Mol. Str. 559 (2001) 209-217.