Optická
reflexe rentgenového a její použití při studiu struktury a teplotní
stability vrstev
Z Bochníček
Katedra
obecné fyziky, Přírodovědecká fakulta MU, Brno, Kotlářská 2, 611
37, Brno
Přednáška představí experimentální
metodu optické reflexe rentgenového záření, její možnosti a omezení.
Při výkladu teorie metody bude více kladen důraz na analogie se
známými jevy klasické optiky a na intuitivní porozumění než na detailní
popis teoretických postupů. Ve druhé části přednášky bude
ukázáno použití rentgenové reflexe při studiu teplotní stability a
interdifuze ve vrstevnatých strukturách.
Optická reflexe rentgenového záření je
experimentální metoda založená na rozptylu záření v blízkosti oblasti
totálního odrazu na rozhraní, tedy při velmi malých úhlech dopadu a
rozptylu. Na rozdíl od klasické difrakce na krystalických strukturách optická
reflexe je na krystalickou stavbu necitlivá a odražená vlna nese informaci
pouze o rozložení středované elektronové hustoty. Metoda je tedy
použitelná i pro amorfní vrstvy, přitom vrstvy samotné jsou z pohledu
rentgenové reflexe homogenní a odražená vlna je dána jen polohou a strukturou
rozhraní elektronových hustot. Detailní popis teorie rtg. reflexe lze najít v
[1].
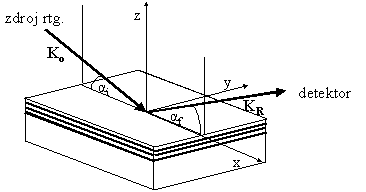
Obr 1: Geometrické uspořádání
optické reflexe rtg záření
Experimentální uspořádání metody je na obr. 1.
Kolimovaný úzký svazek rtg záření
vlnovým vektorem Ko dopadá pod velmi malým úhlem
αi (jednotky stupňů) na povrch vzorku. Odražený
svazek Kh dopadá do detektoru pod úhlem αf.
Volba malého úhlu dopadu je podstatná ze dvou důvodů: jen při
malých úhlech je odrazivost rozhraní dostatečná a současně
při těchto úhlech je hloubka vniku rtg záření do materiálu velmi
malá, což zajišťuje vynikající citlivost metody k ultratenkým povrchovým
strukturám.
Je zřejmé, že intenzita odraženého svazku je nejvyšší
ve směru zrcadlového, tzv. spekulárního odrazu, kdy αf = αi.
Díky nehomogenitám struktury, typicky drsnosti rozhraní, se však rtg
záření po odrazu difúzně rozptyluje a šíří se i do jiných
směrů. Zvláštní význam má rozptyl záření mimo rovinu dopadu. Ten
je využíván metodou zvanou GISAXS (Grazing Incidence Small Angle Scattering),
která slouží zejména pro studium laterálních struktur v povrchové oblasti,
například kvantových teček. Intenzita záření rozptýleného mimo
roviny dopadu však bývá velmi malá, takže tyto experimenty jsou prakticky
omezeny pouze na synchrotronové zdroje rtg záření.
Obr. 2a Obr 2b
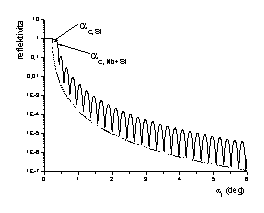
Obr. 2: (a) Závislost spekulární
reflektivity pro čistý povrch Si (čárkovaná čára)
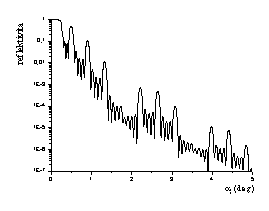
resp. 20 nm vrstvu Nb na Si (plná čára). (b). Reflektivita
multivrstvy Nb/Si.
Na obr. 2a je příklad typické závislosti spekulární reflektivity
(intenzity odraženého záření dělené intenzitou dopadajícího svazku)
na úhlu dopadu αi. čistého dokonale hladkého povrchu Si
(čárkovaná čára) a vrstvy niobu tloušťky 20nm (plná čára).
Pro velmi malé úhly je reflektivita rovna jedné, což odpovídá totálnímu odrazu
na povrchu. Od mezního úhlu pak reflektivita prudce klesá,
v případě Nb vrstvy je pokles modulován oscilacemi, které jsou
důsledkem interference na vrstvě. Pro úhlovou polohu m-tého
interferenčního maxima αim platí vztah
![]()
kde αc je mezní úhel totálního odrazu a t
tloušťka vrstvy.
Obr. 2b pak
znázorňuje spekulární reflektivitu na periodické multivrstvě Nb/Si.
Zde můžeme vidět všechny typické rysy, vypovídající o struktuře
multivrstvy.
- Vysoká úzká
maxima tzv. Braggovská maxima, jejichž poloha je dána periodou
multivrstvy.
- Malé oscilace,
tzv. Kiessigovy proužky, jejichž perioda souvisí s celkovou
tloušťkou struktury. Protože celková tloušťka multivrstvy je n
násobkem periody (kde n je počet period), je perioda malých oscilací N-krát
menší. Mezi dvěma Braggovskými maximy je tak vždy N-2
Kiessigových proužků.
- Modulace výšek
Braggovských maxim (na obr. 2b každé 4. maximum vyhasíná). Tato modulace
souvisí s vnitřní strukturou v rámci každé periody,
odpovídá tedy strukturnímu faktoru, jak jej známe z teorie difrakce.
Platí jednoduché pravidlo: je-li poměr tlouštěk vrstev
v periodě n/m, pak vyhasíná právě každé m+n-té
Braggovské maximum. Multivrstva z obr. 2b tedy má poměr
tlouštěk dNb/dSi v poměru 1/3.
Tvar reflexní křivky je také podstatně ovlivněn drsností
rozhraní a jejich „ostrostí“, tj.strmostí změny elektronové hustoty na
rozhraní. Oba efekty ovlivní rychlost poklesu reflektivity pro větší úhly
dopadu.
Rentgenová reflexe má výsadní postavení
při studiu difúze s extrémně malými difúzními koeficienty.
Při měření na vrstevnatých systémech je možné určit
efektivní difúzní koeficient v řádu 10-27 m2s-1,
což je hodnota o několik řádů nižší než v pro jiné
experimentální metody [2].
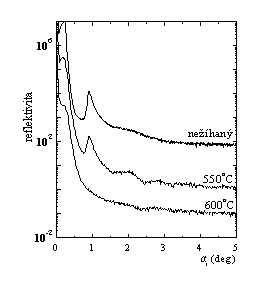
Na obr. 3a je ukázka vývoje reflexní
křivky při žíhání krátkoperiodické vrstvy C-N/Ti-N na vzduchu
pří postupně se zvyšujících teplotě vždy po doby 30 min. Je
zcela zřetelné, že struktura zůstává zachována až do teploty 550oC.
Při žíhání na vyšší teplotě však dochází k její úplné destrukci.
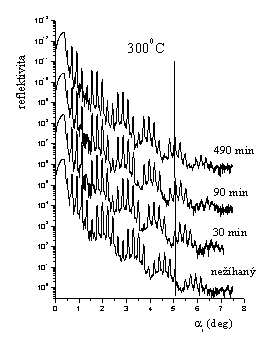
Zajímavější výsledky poskytlo žíhání
amorfní multivrstvy NbSi při teplotách do 350oC (viz obr 3b) [3].
Zde při žíhání nedochází k rozdifundování rozhraní, protože intenzita
Braggovských maxim ani při vyšších úhlech dopadu neklesá. Interdifuzí se
pouze mění poměr tlouštěk složek Nb a Si ovšem tak, že celková
perioda zůstává zachována.
Obr. 3a Obr 3b
Obr. 3: (a) Reflektivita multivrstvy
C-N/Ti-N po žíhání 30 min na uvedených
teplotách. (b). Žíhání
multivrstvy Nb/Si při teplotě 300oC.
Literatura
[1] V. Holý, U. Pietsch, T. Baubach: High-Resolution
X-Ray Scattering from Thin Films and Multilayers. Berlin, Heidelberg, New York 1999. Springer-Verlag,.
[2] A. L.Greer: Diffusion in Artificially Modulated Thin Films. In
Diffusion Phenomena. In Thin Films and Microectronic Materials, Edited. by D.
Gupta and P. S. Hoy, New Jersey 1988.
[3] Z. Bochníček, I. Vávra, Materials Letters,. 45
(2000) 120-124.