Studium magnetických struktur pomocí neutronové difrakce

Karel Prokeš

HMI, SF-2, Glienicker Str. 100, 141 09 Berlín

MFF UK, Ke Karlovu 5, 121 16 Praha

Rozptyl neutronů je jednou z nejrozšířenějších mikroskopických metod v oblasti studia pevných i biologických látek. Je jednou z mála, která je schopna určení prostorového uspořádání magnetických momentů. Hlaními důvody jsou unikátní vlastnosti neutronů. Ačkoliv má neutron nulový celkový elektrický náboj (měření ukazují, že horní hranice činí 10^-21 e), jeho distribuce v prostoru nulová není a neutron má vlastní magnetický moment. V důsledku toho proniká neutron poměrně lehce látkou (je tzv. slabou sondou, což umožňuje např. vytvářet poměrně komplikované termodynamické podmínky vzorku) a interaguje jednak s jádry atomů, jednak s magnetickými momenty elektronů. Navíc, neutrony z běžných zdrojů (reaktory, spalační zdroje) moderované za pokojové teploty mají vlnovou délku i energii srovnatelné s meziatomovými vzdálenostmi a termálními excitacemi v pevné látce. Proud neutronů daných vlastností vykazuje při elastickém rozptylu (t.j. beze změny jejich energie) na pevné látce interferenční jevy které jsou dvojího původu. Je to jednak interference způsobená periodickým prostorovým umístěním atomů podle

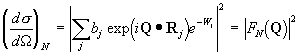(1),

kde b_j značí rozptylovou délku atomu j v pozici R_j v elementární buňce, Q je rozptylový vektor, W_j je Debye-Wallerův faktor a veličina F_N se nazývá nukleární strukturní faktor, jednak interference na rozložení magnetických momentů

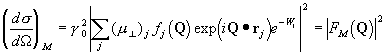(2),

kde g₀ = 2.69 fm a f_j a m_^ značí magnetický form faktor a složku magnetizace kolmou k rozptylovému vektoru. F_M se analogicky nazývá magnetický strukturní faktor. Diferenciální účinný průřez je dán součtem nukleární a magnetické části. Jak je z rovnic (1) a (2) patrné, existuje mezi oběma jevy a rtg. rozptylem blízká analogie. Bez nadsázky se dá říci, že co znamená rtg. rozptyl pro strukturní analýzu, znamená neutronový rozptyl pro magnetickou strukturní analýzu.

Je nutno podotknout, že zatímco nukleární část signálu existuje při všech teplotách a je v podstatě nezávislá na Q, magnetická část existuje jen pod teplotou magnetického fázového přechodu a velmi rychle s Q klesá v důsledku poklesu magnetického form faktoru. Navíc, existuje zde výrazná závislost na směru magnetických momentů. Odečtením referenčního signálu získaného nad teplotou přechodu od signálu získaného pod ním lze v prvním přiblížení získat signál způsobený pouze magnetickými momenty. V případě antiferomagnetické struktury s periodicitou větší než má krystalová struktura, se objeví na difraktogramu nové Braggovy reflexe. V případě rovnosti periodicity magnetické a krystalové struktury (např. při uspořádání feromagnetickém), vzroste jen intenzita některých reflexí.

Úplné určení magnetické struktury sestává ze čtyř kroků: 1, určení teploty magnetického fázového přechodu, 2, určení propagačního vektoru 3, směrů magnetických momentů a 4, určení jejich velikosti a vzájemné fáze.

Bod 1, je téměř vždy alespoň přibližně znám z jiných měření a v difrakčním experimentu jde pouze o ověření zdali teplota přechodu není výrazně odlišná. Určení propagačního vektoru je mnohem náročnější úkol a může představovat nejtěžší krok. V případě práškového vzorku není samozřejmě problém naměřit, pokud to citlivost experimentu dovoluje, magnetický signál a v difraktogramu identifikovat magnetické reflexe pokud jde o magnetickou strukturu souměřitelnou se strukturou krystalovou. Potíže nastávají v případě struktur nesouměřitelných, kdy je možně několik přibližných řešení. V takovémto případě je nutný experiment na monokrystalickém vzorku, u něhož je však prohledávání reciprokého prostoru mnohem náročnější a ne vždy vede k nalezení magnetického signálu. V případě, že je znám propagační vektor, je v principu možné, za pomoci grupové analýzy vytvořit všechny modely magnetických struktur, které symetrie problému povoluje. V případě jednoduchých struktur lye použít intuitivního postupu, který je založen na znalosti typu uspořádání, propagačního vektoru a vyhasínacích pravidel. Fitovacími postupy (především Rietveldovým typem) lze rozhodnout, který model odpovídá nejlépe naměřeným hodnotám. V posledním bodě jde o to rozhodnout, zdali mají magnetické momenty ve všech polohách stejné velikosti a jakou mají vůči sobě fázi, případně, jak je to s populací magnetických domén. Magnetický propagační vektor, který vnáší do struktury novou periodicitu způsobuje v některých případech, že původně ekvivalentní atomy mají neekvivalentní magnetické momenty ať již směrem, velikostí (vzájemný fázovým posunutím), či dokonce že některé z nich jsou geometricky frustrované. Tyto otázky lze zodpovědět práškovým měřením. Otázky populace domén lze osvětlit pouze měřením monokrystalického vzorku. Existují tzv. K domény, lišící se v rámci dané struktury ekvivalentními propagačními vektory a S domény lišící se směry momentů v dané K doméně. Z aobvyklých podmínek jsou domény populovány téměř stejně. Působením magnetického pole či jednoosého tlaku lze populovat či depopulovat některé z domén a odlišit takto magnetické struktury, které jsou charakterizovány jedním K vektorem (s několika K doménama) a několika K vektory v monodoménovém vzorku.

Osnova přednášky:

1, Úvod do neutronového rozptylu (zdroje, vlastnosti neutronů, základní vztahy)

2, Typy magnetických struktur (feromagnety, antiferomagnety, komplexní struktury)

3, Experimentální měření magnetického signálu (instrumentace, referenční signál)

4, Analýza dat - určování magnetických struktur (čtyři body postupu)

5, Problémy spojené s určováním magnetických struktur (problematika domén)

6, Závěr