Rentgenová holografie s atomárním rozlišením

Miloš Kopecký a Jiří Kub

Fyzikální ústav Akademie věd České republiky, Na Slovance 2, 182 21 Praha 8

1. Základní princip holografie

2. Holografie s rovinnou referenční vlnou

3. Holografie s kulovou referenční vlnou

4. Holografie s atomárním rozlišením

5. Virtuální obraz a jeho potlačení

6. Inverzní holografie

7. Experimentální požadavky

8. Rozlišovací schopnost a její závislost na vlnové délce a měřené oblasti k-prostoru.

9. Absorpční holografie

10. Příklad hologramu a jeho rekonstrukce

11. Možnosti klasických zdrojů záření

Úvod

Přestože strukturu většiny materiálů je možné určit pomocí difrakce, existuje řada případů, kdy difrakční metody použít nelze:

(i)  Z některých látek, zejména biologického původu, není možné vypěstovat kvalitní monokrystal a data získaná z práškové difrakce nejsou k úplnému vyřešení struktury dostatečná.

(ii)  Difrakční metody někdy selhávají i v případě monokrystalů díky existenci tzv. „fázového problému“.

(iii)  Klasické krystalografické metody často neposkytují dostatečnou informaci o struktuře neperiodických systémů (jako jsou například amorfní materiály nebo kvazikrystaly), o uspořádání atomů v okolí nečistot a implantovaných iontů, okolí atomů nacházejících se ve velmi tenkých vrstvách, případně adsorbovaných na povrchu vzorku atd.

Proto se hledají stále nové alternativní metody, které by dokázaly rozšířit poznatky o struktuře látek. Jejich příkladem jsou holografické metody s atomárním rozlišením.

Holografické zobrazování

Metoda holografie je známá od roku 1948, kdy ji rozpracoval britský fyzik maďarského původu Dennis Gabor [1] při snaze zlepšit rozlišovací schopnost elektronového mikroskopu. Jeho myšlenka se ale začala uplatňovat v praxi až v šedesátých letech dvacátého století v souvislosti s objevem koherentních zdrojů světla, laserů.

V případě Gaborovy holografie je předmět ozářen rovinnou vlnou. Vlna rozptýlená od předmětu, (předmětová vlna), interferuje s částí dopadající vlny, která projde předmětem neporušena (referenční vlna). Tímto způsobem se převede informace o fázi, kterou nese předmětová vlna, na změny intenzity. Ty je již možno zaznamenat na fotografickou desku nebo jiné záznamové prostředí jako tzv. hologram. K uchování fázové informace je nutné, aby referenční i předmětová vlna byly koherentní, přesněji aby jejich koherenční délka byla větší než rozměry předmětu. Přestože hologram vlastní předmět nijak nepřipomíná, obsahuje veškerou informaci potřebnou k rekonstrukci jeho třírozměrného obrazu. Pokud je hologram ozářen rovinnou vlnou, funguje jako difrakční mřížka, která díky svému sinusovému profilu difraktuje pouze do prvního řádu. Výsledkem jsou dva obrazy, reálný obraz na místě původního předmětu a virtuální obraz na opačné straně fotografické desky. Lze ukázat, že prostorové rozlišení holografie s rovinnou referenční vlnou nemůže být lepší než rozlišení záznamového média [2]. Proto nelze v uspořádání s rovinnou referenční vlnou očekávat dosažení atomárního rozlišení.

Druhým základním typem holografie je Fourierova holografie, kde se jako referenční vlna používá sférická vlna emitovaná kvazibodovým zdrojem. V tomto případě se obraz rekonstruuje pomocí divergentní sférické vlny. V tomto případě není požadavek na rozlišovací schopnost záznamového prostředí tak přísný. Rozlišení Fourierovy holografie je limitováno zejména rozměry zdroje referenční vlny [2].

Hlavní výhodou holografie proti ostatním zobrazovacím metodám je skutečnost, že zaznamenává informaci o třírozměrném předmětu na dvojrozměrnou plochu bez použití optických prvků, tzn. bez aberací. Vzniklý obraz přitom nese informaci nejen o amplitudě ale i o fázi předmětové vlny, což umožňuje prostorovou rekonstrukci předmětu.

Rentgenová holografie s atomárním rozlišením

V roce 1986 přišel Abraham Szöke s myšlenkou, že interferenční obrazce charakteristického rentgenového záření, fotoelektronů či Augerových elektronů vyzářených atomy v pevných látkách jsou v podstatě hologramy, které mohou být využity k prostorovému zobrazení okolí vyzařujících atomů [3]. Jedná se v podstatě o Fourierovu holografii s velmi vysokým rozlišením daným atomárními rozměry zdroje.

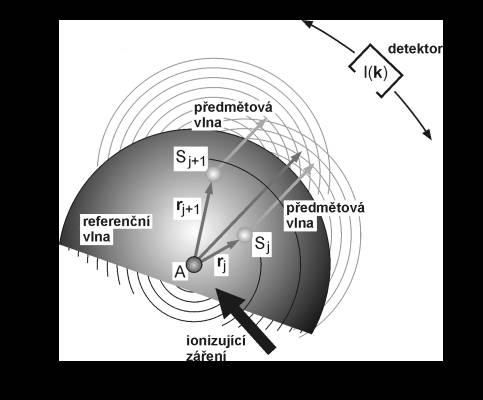
Uvažujme atom A, který vyzařuje buď spontánně nebo díky excitaci ionizujícím zářením z vnějšího zdroje (Obr. 1). Neporušená vlna, která dopadne do vzdáleného detektoru, aniž by došlo k jejímu rozptylu, slouží jako referenční vlna. Zároveň dochází k rozptylu emitovaného záření na ostatních atomech S_j s polohovými vektory r_j, ke vzniku předmětových vln a k jejich interferenci s referenční vlnou. Ze změřené závislosti intenzity na směru vyzařování I(k), kde k je vlnový vektor, je pak možné zrekonstruovat okolí atomu A. Rekonstrukce reálného obrazu (přesněji rekonstrukce rozptýleného vlnového pole) se zde na rozdíl od klasických holografických metod provádí výhradně numericky na základě Helmholtzova-Kirchhoffova integrálního teorému [4]. Tato teorie byla experimentálně potvrzena nejprve pro případ elektronové holografie [5], později bylo úspěšně využito k holografickému zobrazení atomů i rentgenové záření [6]. V roce 1996 bylo navrženo a experimentálně ověřeno inverzní schéma rentgenové holografie [7]. Hlavní výhoda této metody spočívá v tom, že dovoluje měřit hologramy nejen pro několik jeho charakteristických energií, jako je tomu v případě klasické renrgenové holografie popsané výše, ale pro libovolnou energii fotonů nad absorpční hranou vybraného atomu. Přitom rekonstrukce hologramů naměřených při více energiích umožňuje lepší potlačení virtuálních obrazů atomů [8].

Rentgenová holografie poskytuje ve srovnání s elektronovou holografií řadu výhod, ale zároveň přináší i řadu praktických problémů při relizaci experimentu. Rozptyl rentgenového záření na atomech je mnohem slabší a více izotropní než rozptyl elektronů, což umožňuje získat kvalitnější obrazy atomů. Na druhé straně holografický signál od nejbližších středně těžkých atomů tvoří v případě rentgenového záření přibližně jen 0,1 % celkové intensity, což klade vysoké nároky na přesnost měření.

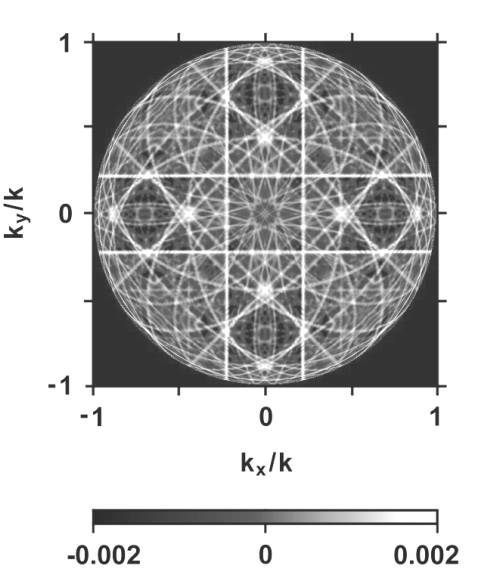
Jako příklad uvedeme využití absorpční holografie [9] k zobrazení okolí atomů kobaltu monokrystalu CoO. Experiment byl proveden v difrakční sekci synchrotronu Elettra v Terstu při energii svazku 13 keV. Změny lineárního absorpčního koeficientu m(k) v závislosti na směru dopadu synchrotronového svazku znázorňuje Obr. 2. Kromě ostrých čar ve směrech, ve kterých dochází k difrakci, jsou zde vidět i pomalejší oscilace. 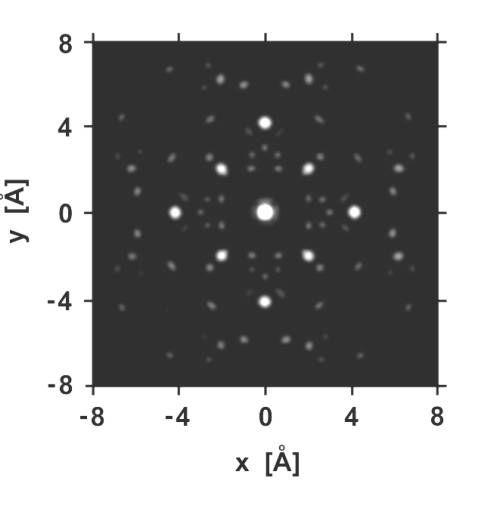Tyto oscilace v rozsahu ±0,2 % tvoří vlastně hologram [9], který lze využít k rekonstrukci okolí atomů kobaltu. Na Obr. 3 je uveden příklad obrazu atomů kobaltu v krystalografické rovině (001). Atomy kyslíku nejsou vidět v důsledku jejich malé hmotnosti.

Závěr

Holografie s atomárním rozlišením je nová metoda, která umožňuje zobrazit okolí atomů vybraného prvku. Přestože se pomocí holografie doposud nepodařilo vyřešit žádnou neznámou strukturu, jeví se tato technika jako velice perspektivní hned z několika důvodů. Na rozdíl od difrakčního obrazu obsahuje holografický záznam informaci jak o amplitudě rozptýlené vlny, tak i o její fázi. Odpadá tak nutnost řešit fázový problém vlastní difrakčním metodám. Holografie nevyžaduje translační periodicitu atomární struktury, čímž se otevírá možnost určovat struktury i organických látek, které nelze zkrystalizovat, či kvazikrystalů, studovat lokální okolí nečistot, implantovaných iontů o malých koncentracích, okolí atomů adsorbovaných na povrchu materiálů atd.

Literatura

[1] D. Gabor, Nature 161, 777 (1948).

[2] G. Faigel a M. Tegze, Rep. Prog. Phys. 62, 355 (1999).

[3] A. Szöke, v Short Wavelength Coherent Radiation: Generation and Application, editoři D. T. Attwood a J. Bokor, AIP Conf. Proc. č. 147 (AIP, New York, 1986).

[4] např. M. Born a E. Wolf, Principles of Optics (Pergamon, Oxford, 1980).

[5] G. R. Harp, D. K. Saldin, B. P. Tonner, Phys. Rev. Lett. 65, 1012 (1990).

[6] M. Tegze a G. Faigel, Nature (London) 380, 49 (1996).

[7] T. Gog, P. M. Len, G. Materlik, D. Bahr, C. S. Fadley, C. Sanchez-Hanke, Phys. Rev. Lett. 76, 3132 (1996).

[8] J. J. Barton, Phys. Rev. Lett. 61, 1356 (1988).

[9] M. Kopecký, A. Lausi, E. Busetto, J. Kub, A. Savoia, Phys. Rev. Lett. 88, 185503 (2002).

Popis k obrázkům:

OBR. 1:  Holografie s atomárním rozlišením.

OBR. 2:  Závislost lineárního absorpčního koeficientu m(k) změřená na planparalelní destičce krystalu CoO při energií svazku 13  keV.

OBR. 3:  Holografická rekonstrukce atomů kobaltu v krystalografické rovině (001).