PROTEINOVÝ DIFRAKTOMETR ≈ MĚŘENÍ ROTAČNÍ METODOU
J. Brynda1
1Department of Gene
Manipulation, Institute of Molecular Genetics, Academy of Sciences of the Czech
Republic, Flemingovo nam. 2, 166 37 Prague 6, Czech Republic
Úvod
Měření difrakčních
dat je základní experiment v krystalové strukturní analýze. Pro struktury
malých molekul jsou běžně měřena data do atomového rozlišení ( většinou do
0.8 Å), takže fázový problém
může být řešen přímo a pozice atomů mohou být rafinovány plně anizotropním
modelem.
Krystaly makromolekul jsou z hlediska
měření difrakčních dat mnohem problematičtější. První problém vyplývá
z velikosti elementární buňky, díky které jsou průměrné intenzity reflexí
mnohem nižší a jejich počet vyšší ( tabulka 1). Za druhé, část objemu krystalu
tvoří kanály vyplněné neuspořádaným rozpouštědlem, takže dále snižují intenzitu
reflexí na vysokém rozlišení a ve většině případů omezují rozlišení na mnohem
nižší než atomové. Za třetí, opět především díky obsahu rozpouštědla, jsou
krystaly citlivé na radiační poškození. Nedávný technický pokrok
v měřících metodách, jako např. používání synchrotronového záření, měření zmražených krystalů a vysoce
účinné plošné detektory, usnadnil
měření, ale to stále zůstává základem celé strukturní analýzy. Proto je
nezbytné tomuto klíčovému kroku věnovat maximální pozornost.
Tabulka 1. Velikost
elementární buňky a
počet reflexí.
|
Sloučenina |
Mřížkový parametr[Å] |
Objem
buňky[Å] |
Počet reflexí |
Prům. intenzita |
|
Organická sl. |
10 0 |
1000 |
2000 |
1 |
|
Supermolekula |
30 0 |
27000 |
30000 |
1/27000 |
|
Protein |
100 0 |
1000000 1 |
100000 |
1/1000000 |
|
Virus |
400 0 |
100000000 |
1000000 |
1/100000000 |
1.
Součásti
proteinového difraktometru
Pro sběr dat
z makromolekulárního monokrystalu při konkrétní vlnové délce potřebujete
difraktometr složený z následujících součástí:
(1)
zdroj RTG
záření
(2)
optickou
soustavu pro fokusaci RTG záření na
vzorek
(3)
monochromátor
pro selekci jedné vlnové délky záření
(4)
kolimátor pro
úpravu rozměrů RTG záření
(5)
„závěrku“
(shuter) pro kontrolu expozice vzorku
(6)
goniostat spojený
s držákem vzorku
Dále je velice vhodné mít k dispozici:
(1)
zařízení pro
měření zmražených krystalů
(2)
účinný plošný
detektor
(3)
software pro
měření, ukládání a zobrazování
exponovaných dat
(4)
software pro
zpracování dat, tj. získání intenzit jednotlivých Braggovských difrakcí a jejich chyb.
2.
Zdroj
RTG záření - rotační anoda
Ve strukturní analýze
makromolekul je praktiky vždy používána
Cu anoda s fixní vlnovou délkou 1.542 Å (pokud není zdrojem synchrotronové
záření). Rotační anoda má proti
klasické rentgence výhodu vyšší intenzity RTG záření. Systémy jsou dnes běžně
vybaveny grafitovým monochromátorem, nebo fokusačními zrcadly, nebo vícevrstvou
optikou (Osmic), které zajišťují fokusaci a
monochromatizaci RTG záření. Velice důležitá je volba apretury kolimátoru,
ta by měla odpovídat velikosti krystalu,
avšak pro velké krystaly s velkou elementární buňkou je lépe požít
kolimator s menší apreturou něž velikost krystalu pro lepší prostorové
rozlišení reflexí.
3.
Goniostat a detektor
Difrakční podmínka je pro
konkrétní reflexi splněna pokud odpovídající bod reciproké mříže protíná plochu
Ewaldovy sféry. Pokud je ozařován stacionární krystal RTG zářením, pak pouze
některé reflexe splňují difrakční podmínku. Proto pokud chceme změřit vetší
množství dat ( pokud možno všechny měřitelné, tj. kompletní soubor dat), musíme
změnit buď velikost Ewaldovy sféry nebo orientaci krystalu. První možnost,
s využitím polychromatického, „bílého“ RTG záření je základ Laueho metody.
Pokud používáme monochromatické záření vybrané vlnové délky, pak musíme
geometrii krystalu během expozice měnit tak, aby byly difrakční podmínky
splněny pro více reflexí. Proteinové difraktometry prakticky vždy požívají
rotaci krystalu a plošný detektor.
Prvním plošnými detektory byly
fotografické filmy automaticky snímané optickými denzitometry. Takto
digitalizované difrakční obrazce byly přeneseny na disk. Hlavní nevýhody
použití fotografických filmů byla pracnost, časová náročnost, vysoké pozadí a
malý dynamický rozsah. Postupně byly vyvinuty další plošné detektory: drátové proporcionální čítače, „Imaging plates“
a konečně CCD detektory ( charge-coupled devices ). Prakticky všechny současné
plošné detektory jsou dnes používány v kombinaci s goniostatem, který
zajišťuje rotaci krystalu okolo jedné osy během expozice. Zbylé přístroje
vyžívají kappa geometrie (ω, κ, φ) kolíbky goniometru pro
nastavení krystalu do další počáteční polohy, ale během měření taktéž rotují
krystal kolem jedné osy.
4. Základy rotační metody
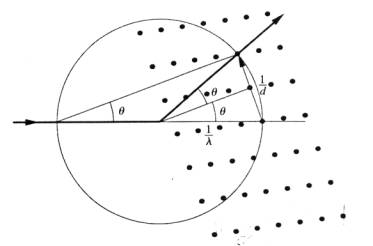 Při použití Ewaldovy konstrukce (obr. 1), která je geometrickou interpretací Braggova zákona, je monochromatické
záření representováno povrchem koule o poloměru 1/l a krystal reciprokou mřížkou. Reciproká
mřížka sestává z bodů ležících na konci vektorů kolmých k difrakčním
rovinám a jejich délka je úměrná převrácené hodnotě mezirovinné vzdálenosti
1/d. Při rotační metodě je krystal otáčen o daný úhel definovaný jako úhel j.
Při použití Ewaldovy konstrukce (obr. 1), která je geometrickou interpretací Braggova zákona, je monochromatické
záření representováno povrchem koule o poloměru 1/l a krystal reciprokou mřížkou. Reciproká
mřížka sestává z bodů ležících na konci vektorů kolmých k difrakčním
rovinám a jejich délka je úměrná převrácené hodnotě mezirovinné vzdálenosti
1/d. Při rotační metodě je krystal otáčen o daný úhel definovaný jako úhel j.
Obr.1 Ewaldova konstrukce. Bod reciproké
mřížky leží na povrchu Ewaldovy sféry pokud je splněna následující trigonometrická
podmínka: 1/2d = (1/l)
sinq. Po
jednoduché úpravě dostaneme Braggovu rovnici:
l = 2d sinq.
Takže pokud bod s indexy hkl reciproké mřížky leží na povrchu Ewaldovy
sféry, je splněna difrakční podmínka a dojde k difrakci v daném směru.
Pro krystal v jedné
orientaci bude pouze malá část reflexí splňovat difrakční podmínku. Počet
reflexí bude velice malý pro malé molekuly (v některých orientacích i nulový).
Krystaly makromolekul mají však větší elementární buňky (a, b, c v řádu 100
Å), pokud srovnáváme s vlnovou délkou použitého záření, což
v geometrické interpretaci znamená, že reciproká mřížka je velice hustě
zaplněna vzhledem k velikosti Ewaldovy sféry. Z toho vyplývá, že
mnoho reflexí difraktuje současně do různých směrů, jelikož mnoho bodů reciproké
mřížky leží současně na povrchu Ewaldovy sféry. To také vysvětluje výhodu
velkých plošných detektorů pro měření krystalů s velkou elementární
buňkou.
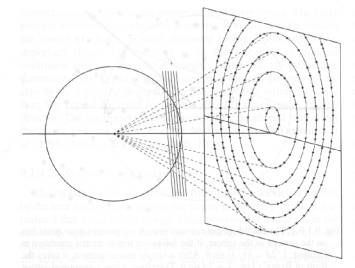
Obr. 2 Rovina
reflexí, která je přibližně kolmá k záření dá vzniknout elipse reflexí na
detektoru.
Body reciproké mříže leží
v rovinách, takže protínají Ewaldovu sféru v kružnicích. Odpovídající
difraktované reflexe z centra Ewaldovy sféry tak tvoří kužely a jelikož
při většině experimentů je detektor umístěn kolmo na směr primárního svazku
záření, tvoří reflexe rovin elipsy (viz obr. 2). Pokud některá osa krystalu
leží téměř paralelně s primárním zářením, elipsy vytvářejí soustředné
kruhy s centrem ve středu detektoru. Všechny reflexe ležící na jedné
kružnici (elipse) mají jeden index společný a pro necentrované buňky postupně
vzrůstá o jednotku. Vzdálenosti mezi kruhy závisejí na převracené hodnotě
parametru rovnoběžného s primárním zářením.
4.1. Mosaicita krystalu a divergence záření
Při Ewaldově konstrukci
předpokládáme ideální zdroj záření s totálně paralelním zářením a ideální
krystal se všemi elementárními buňkami stejně orientovanými, takže výsledkem by
byly bodové, nekonečně ostré Braggovské difrakce. Reálné experimentální
podmínky se od tohoto ideálu liší ve třech aspektech. Za prvé, dopadající
záření není nikdy dokonale paralelní, za druhé, reálné záření není striktně
monochromatické a za třetí, reálné krystaly jsou tvořeny malými mosaikovými
bloky, které nejsou vzájemně přesně stejně orientované. Pokud měříme krystaly
makromolekul při laboratorní teplotě je rozpětí vzájemné orientace mosaikových
bloků (mosaicita) většinou do 0.05o, ale pokud krystaly měříme
zmražené může mosaicita vzrůst až na 1o i více. Všechny tyto efekty
( schemataticky znázorněné na obr. 3) rozšiřují difrakce na větší rozsah rotace
krystalu.
4.2. Rotační snímky a „lunes“
Pokud chceme změřit
další reflexe, které v danné orientaci neleží na povrchu Ewaldovy sféry,
při použití monochromatického záření, musíme krystalem otáčet aby pro další
reflexe byly splněny difrakční podmínky. Pokud je krystal otáčen okolo jedné
osy během po sobě následujících
expozicích, jedná se o rotační metodu. V praxi je
rotační osa je skoro vždy osa
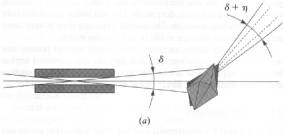
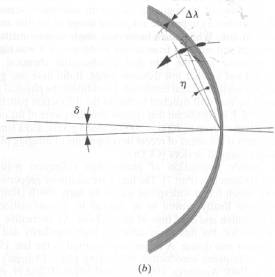
Obr. 3 Schematické znázornění divergence záření d a mosacity krystalu h. (a) V přímém prostoru, (b) v reciprokém
prostoru, kde je Ewaldova sféra rozšířena díky konečné šířce pásu použité
vlnové délky dl/l.
rotace kolmá k dopadajícímu
záření, tak aby byla zachována symetrie mezi oběma polovinami kompletního
snímku. Toto je nejčastěji používaná metoda při měření difrakčních dat krystalů
makromolekul. Pokud je krystal rotován během expozice, elipsy popsané pro fixní
pozici krystalu mění svojí pozici. Výsledkem je, že snímek vzniklý během
expozice obsahuje všechny difrakce mezi
dvěmi limitními pozicemi elips na začátku a konci daná rotace, které tvoří tzv.
„půlměsíce“ ( lunes ).
4.3.Částečně a úplně změřené difrakce
Při rotační metodě
vznikají „lunes“ jež obsahují difrakce mezi elipsami vzniklými mezi místy,
která byla na Ewaldově sféře proťata
danou rovinou reciproké mřížky
mezi začátkem a koncem rotačního intervalu Δφ. Pokud byla
Ewaldova sféra proťata daným bodem reciproké mříže kompletně, je změřena úplně
a naopak, pokud bod reciprokého prostoru prošel jen z části Ewaldovou
sférou, dokončí průchod při další rotaci a daná reflexe je na jednotlivých
rotačních snímcích registrována po částech. Vzhledem k velké hustotě reciproké
mříže je nemožné změřit všechny reflexe naráz během jedné velké rotace, jelikož by docházelo k překrývání difrakcí.
Na šířku „lunes“ má
zásadní vliv mosaicita krystalu (vliv divergence a mosacity nelze jednoduše
separovat, navíc divergence je prakticky konstantou pro daný zdroj a je
většinou zanedbatelná ve srovnání s mosaicitou), pokud je mosacita malá jsou
„lunes“ úzké, naopak velká mosaicita značně rozšiřuje plochu „lunes“ (viz obr.
4).
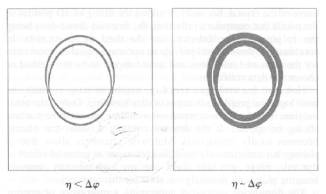
Obr. 4 Vzhled „lunes“: (a) krystal s malou mosaicitou, (b) krystal
s velkou mosaicitou.
4.4.
Velikost rotačního intervalu
Zásadním parametrem rotační metody je velikost rotačního intervalu na jednotlivou expozici. V praxi existují dva základní přístupy: velké a malé rotační intervaly (v originále wide and fine slicing φ ). Obě metody mají své výhody i limitace. Jemné vzorkování minimalizuje pozadí, umožňuje přesné fitování difrakčního profilu ve φ. Hrubé vzorkování je vhodné pokud doba čtení z detektoru je relativně dlouhá a dále většina reflexí je změřena jako úplně změřené. Na obr.5 můžete vidět vliv velikosti rotačního intervalu na šířku „lunes“.
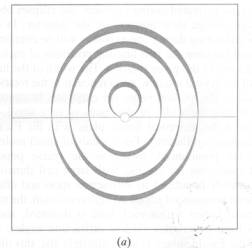
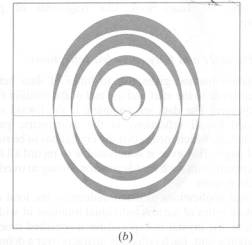
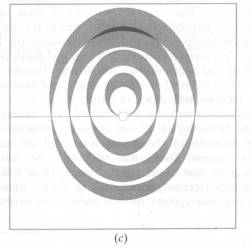
Obr. 5 Šířka
„lunes“ je úměrná Δφ (rotačnímu úhlu na jednu expozici). Velikost
Δφ (rotační úhel na jednu expozici) roste od (a) do (c), až u (c)
dochází k překryvu.
4.4.Vzdálenost krystal detektor
Dalším zásadním parametrem
rotační metody je vzdálenost od krystalu
k detektoru (d). Na všech difraktometrech pro měření makromolekulárních
krystalů je tato vzdálenost měnitelná, většinou je minimální vzdálenost
limitována možnou srážkou detektoru s goniometrem nebo chlazením a
maximální vzdálenost je dána konstrukční volbou výrobce. Čím kratší je d, do
tím většího rozlišení je možno měřit. Jelikož je však rozlišení téměř vždy
limitováno difrakční kvalitou vzorku, je vhodné nastavit vzdálenost tak, aby
byla vhodně využita celá ploch detektoru (jak praví klasici proteinové
krystalografie: „Je důležité měřit intenzity, nikoli indexy“.). S d
souvisí i prostorové rozlišení jednotlivých difrakcí. Další fakt, který je dobré vzít do úvahy je fokusace svazku
záření, pokud je záření fokusováno na určitou vzdálenost, pak jsou difrakce
nejlépe prokresleny v této vzdálenosti.
Literatura : International Tables for
Crystallography, Volume F, 177 - 195